铁路隧道电分相结构参数与中性线过电压研究
郑景文,刘明光,崔玮辰,彭 伟,黄文勋,王 强
(1.北京交通大学电气工程学院,北京 100044; 2.轨道交通工程信息化国家重点实验室(中铁一院),西安 710043)
1 概述
山区高海拔地区的铁路(如川藏铁路)是我国西部大开发的重要战略线路。由于海拔高度相差大,长大坡道连续,隧道群密集,造成牵引供电设施选址较为困难,有些电分相不得不设置在隧道内。由于关节式电分相的中性线与接触线相互平行,且间距较小(约为500 mm),中性线对地、对接触线都会构成等值电容,当这些等值电容存储一定数量的电荷时,中性线对地就会表现出感应电压,可能高达数千伏。中性线感应电压直接影响到动车组(或电力机车)过分相时产生的过电压大小,过电压可能造成牵引变电所误跳闸,车顶绝缘设备击穿,以及电分相线索烧损等故障[1-3]。因此,准确计算电分相中性线的电气参数和过电压,对电分相设计及其安全运行,具有重要的现实意义。
七跨绝缘锚段关节式电分相(以下简称“七跨关节电分相”)在铁道牵引供电网中得到普遍应用[4-5],本文以七跨关节电分相为例,分别计算隧道内外电分相中性线等值电容、感应电压,对比分析两者的相对差,并在仿真软件PSCAD中搭建动车组过分相的仿真模型,比较研究隧道对电分相过电压的影响。
2 电分相中性线感应电压产生的机理
两平行接触线,带电接触线通过空间静电感应和电磁感应,对相邻停电接触线产生感应电压[6],如图1所示。
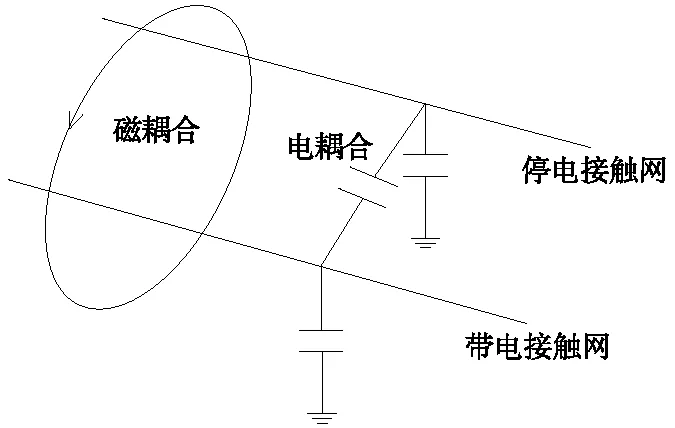
图1 电磁耦合示意
由于动车组进分相前,接触线中电流产生的交变磁场不切割中性线,可忽略中性线和接触线的磁耦合,只考虑接触线与中性线的电耦合。而中性线自感和电阻远小于容抗,因此,在计算中性线感应电压时,可以忽略中性线和接触线的电阻和自感。计算电分相中性线感应电压的简化电路如图2所示[7-9]。

图2 电分相简化电路

节点1的节点电压方程为

(1)
式中,ZNJ=1/jωCNJ;ZN=1/jωCN;代入式(1),整理可得电分相中性线感应电压UN的表达式
(2)
3 电分相中性线等值电容计算
3.1 地面上方的导线等值电容计算法
地面上方相距D、对地高度h的两条导线(可以视为接触线和中性线),可利用镜像法来计算其对地等值电容[10-12],如图3所示。
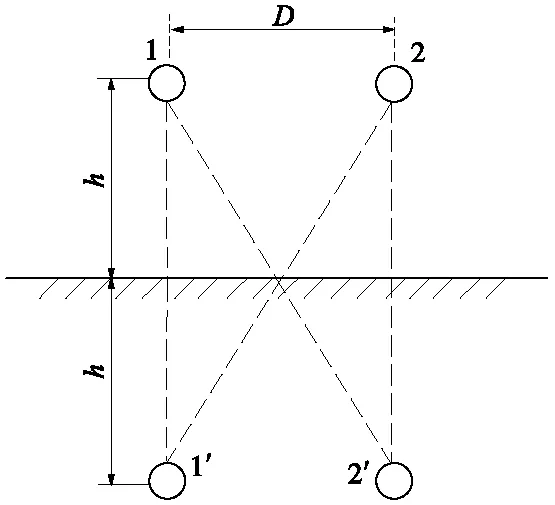
图3 平面大地镜像
以大地为零电位参考面,两导线的电位与电荷之间有下列关系[6]
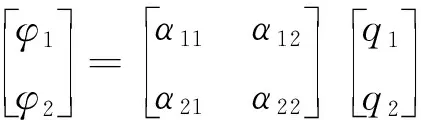
(3)
式中,φ为导线电位;q为导线电荷;α为电位系数,字母的下标数字表示导线编号;电位系数矩阵[α]中α11、α22为自感应系数,α12、α21为互感应系数。
将式(3)左乘[α]-1可得
(4)
式中,β为静电感应系数,[β]=[α]-1。
电荷q、电容C和电压U满足以下关系式
(5)
式中,C11、C22为导线对地电容;C12、C21为导线的互电容,根据静电场互易原理,C12=C21;U1、U2为导线对地电压;U12、U21为导线对地电压差值。已知大地为零电位参考面,则U1=φ1-0、U2=φ2-0、U12=φ1-φ2、U21=φ2-φ1,式(5)可改写为
(6)
联立式(4)求得

(7)
根据电磁场理论,平面大地上导线的自电位系数αs和互电位系数αm分别为[13]
(8)
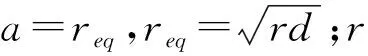
将式(8)代入式(3),联立式(4)、式(7),求得电分相中性线对地电容CN1、与接触线之间的电容CNJ1为

(9)
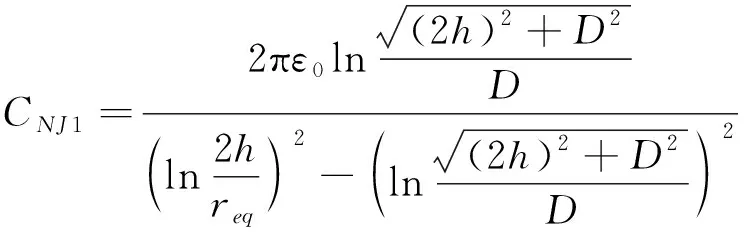
(10)
3.2 计入隧道影响的导线等值电容计算法
典型的隧道截面如图4(a)所示,隧道内接触网导线的四周都是大地结构,因此导线的各个方向都存在对地电容。参考平面大地的镜像法,在保证隧道中接触网导线相对位置不变的条件下,将隧道按等周长原则等效为如图4(b)所示的圆形隧道[14-16],推导出圆形隧道内导线的电位系数,进而计算等值电容。由于隧道截面的几何尺寸比隧道中接触网导线截面大很多,在计算中,可以假设隧道中的接触网导线和圆形等效隧道无限长,且导线与隧道平行。

图4 隧道等效断面示意(单位:mm)
导线i代表接触线,导线k代表中性线。由于电位系数是与导体的电位和带电量无关的常数[17],为方便计算圆隧道内导线的电位系数,假设导线i的电荷密度为ρ,导线k的电荷密度为零。导线i与圆心距离为d,导线等效半径为a。为消除接隧道的影响,镜像线电荷应位于圆形隧道外,假设镜像i'的线电荷的密度为ρ',与圆心的距离为d',如图5所示。

图5 圆形隧道镜像
以隧道壁为零电位参考面,根据电磁场理论可知,圆柱内任意一点M的电位为[9]

(11)
圆隧道壁上任意一点M'的电位为零,即
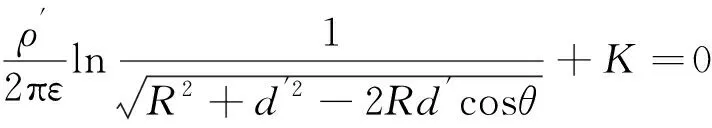
(12)
上式对于任意θ都成立,所以dφM′/dθ=0,即
ρd(R2+d′2)+ρ′d′(R2+d2)-
2Rdd′(ρ+ρ′)cosθ=0
(13)
为探索式(13)中θ与2Rdd′(ρ+ρ′)等参数的关系,式(13)两边对θ再次求导,可得
2Rdd′(ρ+ρ′)sinθ=0
(14)
式(14)存在2组解:(1)当sinθ=0,即θ=kπ,k=0,1,2,3,…时,2Rdd′(ρ+ρ′)为任意实数;(2)当θ≠kπ时,2Rdd′(ρ+ρ′)=0。又因为对于任意θ,式(14)恒成立,所以2Rdd′(ρ+ρ′)的通解为以上2组解集的交集,由2Rdd′≠0,解得:ρ′=-ρ。
将ρ′=-ρ代入式(13),有
ρd(R2+d′2)+ρ′d′(R2+d2)=0
(15)
解得:d′=R2/d;由式(12)可知φM′=0,则K=ρ/(2πε)ln(d/R)。将以上各解代入式(11)可得
(16)
根据电位系数定理,隧道内的导线的自电位系数和互电位系数为

(17)

(18)
根据图4(b)可知,接触线和中性线到圆心的距离相近,为简化计算,认为两者在同一圆周上,即d=dk。将式(17)和式(18)代入式(3),联合式(4)、式(7)可得隧道内电分相中性线对地电容CN2、与接触线之间的电容CNJ2为
(19)
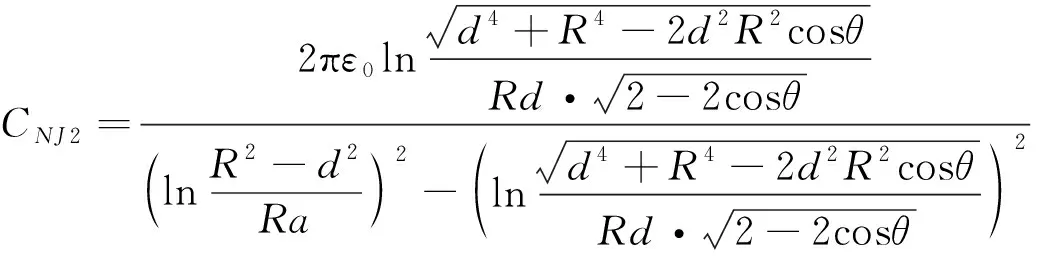
(20)
4 中性线等值电容参数和感应电压计算
4.1 等值电容参数计算与分析
典型的七跨绝缘锚段关节式电分相的结构参数为:中性线悬挂高度h为6 000 mm,中性线与接触线平行间距D为500 mm,中性线等效半径req取94.87 mm,中性线长度为350 m,中性线与接触线导线的平行长度为150 m。将以上参数代入式(8)、式(9)、式(19)、式(20),可以分别计算出隧道外和隧道内单位长度(m)的中性线对地电容CN和单位长度(m)的对接触网导线的互电容CNJ,如表1所示。

表1 中性线分布电容 pF
由表1的计算结果可知,在中性线悬挂高度h、等效半径req、与接触线间距D相同时,隧道内中性线对地电容比隧道外中性线对地电容增大61.57%,中性线与接触线的互电容减小15.11%。
4.2 中性线感应电压计算与分析
(1)隧道外的电分相
隧道外电分相中性线感应电压(记为UN1),按照本文方法计算为

(21)
实测感应电压的范围较大(3~14 kV)[9,18],平均值为8 kV。计算值与实测值的相对误差为

(22)
(2)隧道内的电分相
隧道内电分相中性线的感应电压(记为UN2),按照图2计算得

(23)
计算值与实测值的相对误差为

(24)
(3)分析
相同结构的电分相在隧道内和隧道外时,中性线的感应电压大小不同:隧道内为6.4 kV,隧道外为8.6 kV,两者的相对差为2.2 kV。产生这样的结果主要原因是:隧道改变了隧道内中性线在空间产生的电场分布,使中性线的对地电容增大,互电容减小,最终使电分相中性线的感应电压减小。
5 隧道对动车组过分相过电压的影响
CRH5G动车组能够在-40 ℃高寒条件下运行,且具有抗风沙等恶劣环境的特点[19],因此,本文以CRH5G型动车组通过电分相为例,在PSCAD中搭建动车组过分相的仿真模型[20-21]。在动车组断电过分相时,对比隧道外和隧道内两种仿真模型的电分相中性线的过电压。中性线过电压仿真波形如图6所示。

图6 过电压波形
根据仿真结果可知,隧道内电分相中性线过电压的最大值约为115.5 kV,隧道外电分相中性线过电压的最大值约为83.7 kV,前者比后者高出38%,约31.8 kV。
保持仿真条件不变,再以CRH380A、CRH2E、CRH3C为例,仿真不同型号动车组分别通过隧道内和隧道外的电分相时,中性线过电压的仿真结果如表2所示。

表2 中性线过电压
对比表2的仿真结果可知,不同车型动车组通过电分相时,隧道内电分相出现的过电压比隧道外电分相出现的过电压大,大致高出30%~40%。
6 结论
(1)电分相中性线的分布电容受隧道的影响较大,不计隧道时,对地电容为6.938 pF/m,互电容为13.275 pF/m;计入隧道影响时,对地电容为11.210 pF/m,互电容为11.269 pF/m,后者比前者的对地电容增加61.57%,互电容减小15.11%。
(2)不考虑隧道影响时,电分相中性线感应电压约为8.6 kV,考虑隧道影响时,中性线感应电压约为6.4 kV,后者比前者降低约25.6%。
(3)在接触网的电分相结构相同条件下,动车组通过隧道内的电分相,比通过隧道外的电分相出现的过电压会高出30%~40%。这在设计电分相结构和运行维护时,应该引起足够重视。

