深水立管入水过程中涡激耦合振动特性分析
张 颖,朱卫平
上海大学,力学与工程科学学院,上海市应用数学和力学研究所,上海市能源工程力学重点实验室, 上海
1. 引言
石油作为当今社会最常用的能源之一,也是经济和社会稳定发展的重要战略资源。陆地及浅海石油资源的勘探已经日渐成熟,然而对于更深水域石油资源的争夺与勘探日趋变为各国的战略需求。而当石油勘探转移到海上领域,就会利用到动态定位平台。动态定位平台可以工作的最大水深在理论上是不受限制的,但实际上存在两个限制:船用立管的长度限制,张紧器和升沉补偿器的性能限制。目前,地球上拥有丰富的海上石油和天然气资源,并且可能大多数都在深水之下,这驱使勘探工作进入到深海甚至超深水领域,一些研究已拓展到3000 m 的范围[1]。深水钻探立管是连接在海底井口和浮动钻探平台之间的重要设备。因此,迫切需要对海洋深水和超深水钻井设备进行开发[2]。而在开发进程中,如果载荷计算不准确,强度设计不合理,将给深水钻井作业带来安全隐患。此前在墨西哥湾和巴西海的钻井过程中,就因为进料塔的故障造成了巨大的经济损失和环境破坏[3] [4]。
作为深海石油勘探必不可少的设备(如图1),钻井立管是从海床井口到钻探平台的主要连接通道,与泥浆的控制出口相连,在深水中承受多种载荷,包括风,浪,潮和尾迹的流体动力,泥浆和管道的重力和浮力,以及平台张紧器施加的张力,立管内外压差和上下温差等,这些状况都与水深有关。在深水中,比如水深达3000 m,立管的纵横比(L/D)将高达6000,是典型的三维柔性液固相互作用的结构。当水流流过垂直立管时,通常有涡从立管表面频繁脱落,从而形成涡流。涡流激励立管在横流(cross-flow, CF)方向振动,而来流则引起立管在流线(in-line, IL)方向的运动。涡激振动(vortex-induced vibration, VIV)是一种典型的自激振动,如果涡脱落频率接近立管的固有频率之一,则会发生频率锁定现象[5],这将加速结构的疲劳损伤,可能导致无法估量的损失。
计算流体动力学(CFD)直接数值模拟(DNS) [6] [7] [8] [9] [10]被认为是预测细长立管VIV 现象的理想方法。但是,由于三维DNS 对计算资源的需求太高,从而限制了对在实际雷诺数和实际纵横比的情况下油气深水勘探立管的模拟,导致这种贴合实际工况条件下的模拟至今仍然很少。为了满足当前的要求,本文使用van der Pol 振子方程(范德波尔方程)来模拟VIV 在结构上的涡激效应,这可以大大节省计算需求并能捕获涡激效应的主要特征。利用范德波尔振子来模拟涡激振动对结构的影响已经被前人广泛地讨论[5] [11] [12],如Wang 等人[13]为研究内部输运流体的柔性管道涡激振动引起的屈曲,发展了一种三维计算模型和伽辽金解,其中与涡动力相关的非定常水动力用两个范德波尔振子进行模拟,立管为两端铰支,L/D = 200。然而,当轴立管直径为非均匀,部分安装浮力块,以及更复杂的载荷和边界条件时,例如:在受到剪切流和非均匀压力,以及立管因海上平台漂浮而振动,下端悬重摇摆和向下运动等情况下,伽辽金方法已难以解决。因此在本文中,我们首先基于哈密顿原理建立相应的动力学方程,然后采用有限元法(FEM)离散方程,将涡激振子也离散到各结点上,从而让复杂的载荷和边界条件变得易于处理,便于模拟和分析局部带有浮力块的立管在下入过程中含涡激耦合效应的力学行为。本文提出的模型和解法具有模拟纵横比大于6000 的立管对所有上述载荷和边界条件的VIV 响应的能力,为以后的海洋钻探系统研究和应用提供了强大的计算平台。

Figure 1. Schematic of the fluid-conveying riser subjected to currents and the wake 图1. 作业立管的结构、载荷及坐标系意图
2. 模型与求解
2.1. 立管振动模型
本文分析模型中,定义水平面上为y 和z 轴,垂直方向上为x 轴(如图1),根据哈密顿原理,考虑管内流体压力、密度、流速和温差的动力学方程可表示为


采用空间细长梁单元将立管离散为有限元模型。设其形函数为Nx(x),对式(1)在一个单元上进行积分,可得

其中




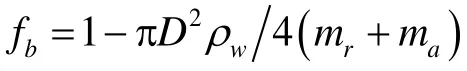

在这里, fD0是平均阻力, fD是涡流引起的波动阻力, fL是管道上的升力。 这些可以表示为

其中, CDi是随时间变化的涡流诱导阻力项,CD0是两端固支管道的平均阻力系数, CL是升力系数。 CDi和 CL可以表示为

其中 CDi0和 CL0是两端固支立管相关的发生涡旋脱落的非稳态阻力和升力系数。 p ( x, t )和 q ( x ,t )分别代表在y 和z 方向上的涡激变量,其模型将在下一节详述。
顺便指出,在式(16)中,当立管被外径为Db的浮力块所包裹时, D = Db;如果立管或立管的一部分中没有浮力块,则D 即为立管的外径。
此外,当立管的挠度变大时,挠度斜率将改变载荷的分布,因此,应将式(14)和(15)所表示的结点力分量可修正为

2.2. 范德波尔尾迹振子模型
式(17)中两个尾迹变量 p ( x,t )和 q ( x ,t )为无量纲量,可由以下两个van der Pol 方程控制[14]:


St称为斯托哈尔(Strouhal)常数,与雷诺数Re 有关,在 Re= 2 × 102-2 × 105范围内(本文所属范围),St可近似取0.2 [15] [16]。
2.3. 方程求解

i) 求解方程(2)齐次式的特征值,获取立管的最低第一和第二角频率 Ωr1和 Ωr2,然后通过式(8)计算[ cs];
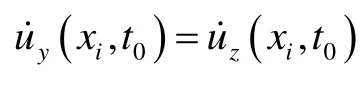
iii) 计算式(4)~(7)和(9)~(18),并将其代入公式(2)中;
v) 用Runge–Kutta 方法求解方程(19)和(20),提取 p ( xi,tk)和 q ( xi,tk),然后将它们代入方程(13)~(18)和(2)中,完成一个循环。让 tk+1= tk+∆t (可设 ∆t = 0.01s )。转回到步骤iv)继续循环计算,直到 tk+1= 60 s 。
下标 i = 1,2,… ,N ,N 表示有限元结构中的节点数;k = 0,1,… ,N′,N′是从0 到60s 的时间步长总数。通常,在求解式(2)之前,必须将局部单元坐标表示的所有相关矩阵和向量转换为全局结构坐标,并集成到结构矩阵和向量中。
2.4. 模型验证和参数设定


Table 2. The maximum root-mean-square amplitudes for the model 表2. 最大振幅均方根对比


Table 3. Coefficients for the dynamic models 表3. 模型主要参数值
以上与实验,计算和解析解方法得到的结果比较证明,本模型包括算法和编程是可信且有效的。在下一节中,我们将使用本方法来计算和讨论钻探立管在深水区下落时的动力学响应,以及带浮力块的钻井立管的力学行为分析。
3. 钻探立管在深水区下入时的动力学响应
3.1. 计算方案

另外,假设在深水条件下,由波浪引起的水质点运动的速度遵循平面波的线性理论,例如,在xy 平面内,在水深x 和时刻t,速度uy为[20]

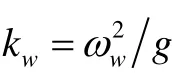

其中vm和vt是水面上风流速和潮流速。在本文中,设 Hw=6.5 m ,Tw=13s ,vm= 0.2 m s ,vt= 3.5 m s ,并且假定潮流速的方向与y 轴平行,风引起的流速和波浪引起的流速方向一致且与z 轴平行。其他主要参数值见表3。
3.2. 代表性结果
为了对本模型模拟情况有一个大致了解,图2(a)~(h)给出了带有浮力块的立管进入到1000 米水深时几个典型的动力响应图形和曲线,此时上端送入速度 u0= 0。浮重比 RBW= 0.5,对应的浮力块总长Lb= 315 m (图2(a)和图2(b)绿色原点组成的长度)。图2 的图题中简要说明各子图(a)~(h)的含义。值得注意的是,增加浮力块虽然可以减轻张紧器和平台的负担(如图2(i)),但会增加海流对立管的尾迹效应(如图2(f)~(h)),增大下端横向位移(如图2(a)~(d))和局部弯曲应力(如图2(e),图2(j)),从而增加下入立管对水下井口的对准难度,还可能加速立管的疲劳损伤。

3.3. 立管上端送入速度和下端悬挂重量的影响
本节假设水深(管长) L = 3000 m,管下端悬挂重量分别为Pex = 1000 kN、2000 kN 和3000 kN,不加浮力块,流速等其他条件如在3.1 所述。当立管下入到接近3000 m 时,设立管上端的送入速度分别为u0= 0,u0= 0.15 和u0= 0.3 m/s,以此为初始条件模拟60 s。考察这后20 s~60 s 立管的下端最大横向位移、上端的最大拉伸应力和全管最大弯曲应力,比较结果如图3 和图4 所示。可见,在悬吊重量相等的情况下,u0的增加会使最大y 方向的位移uy略微降低(图3(a)),而最大uz几乎没有受到影响(图3(b))。随着u0的增加,最大弯曲应力(图4(a))和最大拉伸应力(图4(b))略有下降。此外,Pex 的增加使得最大uy(图3(a))和最大拉伸应力(图4(a))都稍微下降,并使得最大弯曲应力也显著降低,比如,与Pex = 1000 kN 相比,Pex = 2000 kN 时下降27.6%,Pex = 3000 kN 时下降53.8%。这是因为IL 流向是在y 方向上,导致垂直立管向该方向弯曲,而较大的Pex 大大降低了IL 流弯曲立管的弯曲曲率并有使立管向铅垂线靠拢的趋势,因此,uy和弯曲应力减小。对于较大的u0和Pex 下的拉应力的降低,前者是由于水的轴向阻尼作用,而后者是由于悬重可以抑制轴向振动的幅值而发生的。从图4 中可明显得出Pex 越小,振幅越大,最大拉应力越大;Pex 越大,振幅越小,最大拉应力越小。此外,较大的Pex 增加了负z 向的最大位移,如图3(b)所示。立管z 向位移可以归结为流体动力fz,即等式(15)~(17)中定义的尾流动力。由于较大的Pex 减小了立管的弯曲曲率,且垂直直管的尾迹效应大于倾斜直管[21],因此会产生uz。然而,最大的uz与最大的uy数值量级相比很小,可以忽略不计。
因此,适当增加下入速度和悬重可以降低最大弯曲应力和最大拉力应力,只要上部平台和张紧器足够强,几乎不会对立管进入产生负面影响。

Figure 3. The riser maximum displacement uy in the incoming flow/y-direction (a) and uz in the CF /z-direction (b), which vary with the bottom-end hanging weight/load (Pex) and entry speed (u0) in 3000-m-deep water 图3. (a) 立管下端在来流(y)方向上的最大位移uy 和(b) 在横流(z)方向上的最大位移uz 随底端悬重(Pex)和上端送入速度(u0)的变化

Figure 4. The riser maximum tension stress (a) and maximum bending stress (b), which vary with the bottom-end hanging weight/load (Pex) and entry speed (u0) in 3000-m-deep water 图4. (a) 立管最大拉应力和(b) 最大弯曲应力随底端悬重(Pex)和上端送入速度(u0)的变化
3.4. 不同水深和悬重的影响
设水深分别为500 m,1000 m,1500 m,2000 m,2500 m,3000 m。当立管下入到对应的水深时,停止送入(u0= 0),以此为初始条件再模拟60 s,考察这后20 s~60 s 立管的下端最大横向位移、上端的最大拉伸应力和全管最大弯曲应力。立管上不加浮力块,下端悬重不同,分别为Pex = 1000 kN,2000 kN,3000 kN,海况等其他条件如第3.1 小节所述。比较结果如图5 和图6 所示。
从图5(a)可以看出,当Pex 为常数时,最大uy随着L 的增大而增大。在L = 3000 m 时的最大uy是在L= 500 m 时的2.5 倍。随着L 的增大,最大uy的增大率明显减小。此外,当L 保持恒定时,最大uy随着Pex 的增大而减小,因为较大的Pex 减小了底端位移(例如,当L = 3000 m 时,Pex = 3000 kN 时的最大uy是Pex = 1000 kN 时的0.9 倍)。

Figure 5. Maximum displacement of uy and uz varying with riser length (L) and hanging weight (Pex) at u0 = 0 in the y- (a) and z-directions (b) 图5. (a) 立管底端的y 方向(uy)位移和(b) z 方向(uz)位移随管长度(L)和悬重(Pex)的变化

与图5(a)中的uy相比,图5(b)中最大uz的变化较为复杂。uz在CF 方向上,主要受复杂的尾迹控制,而uy在IL 方向上,主要受来流影响。比较(a) (b)中uz和uy的数量级,此时尾流效应可忽略不计。
图6(a)为最大拉伸应力随着L 的增大而增大,符合预期结果;但随着吊重的增加,最大拉应力略有下降,此现象可归因于吊重抑制了立管的轴向振动。
从图6(b)可以看出,随着L 的增大,最大弯曲应力基本保持不变,但随着悬挂重量的增加而显著减少。其原因可以归结为最大弯曲应力取决于立管的曲率,前者,增加L 可能会增加横向位移,但曲率本身可以保持不变;后者,是因为吊重可以将弯曲的立管拉直,从而降低立管的曲率和弯曲应力。
4. 结论
本文针对内部输运流体的柔性立管发展了一种新的VIV (涡激振动)三维动力学模型,以便能模拟立管在实际环境条件下进入深度为3000 m 甚至更深的水中时的动力学响应。重点讨论了悬重、下入速度以及水深对立管底端横向位移(事关防喷器的落点与下井口的对准和控制)以及立管上端最大拉应力(涉及张紧器和平台的提升能力)和最大弯曲应力(涉及立管的疲劳损伤)的影响,并得出如下结论:
1) 在一般海况下,将钻探立管下入到深水中时,降低下入速度对落点偏移量没有明显的影响,但可以少许减小局部最大弯曲应力;
2) 尽管深水需要较长的钻探立管,但长度大的立管自重也大,增加了下垂能力,因此不会增大落点的偏移量;
3) 当水深一定时,增加悬重可以减小落点偏移量,但立管的上端拉力会随悬挂重量的增加而增加,因此需要更强劲的张紧器和排水量更大的平台;
4) 增加浮力块虽然可以减轻张紧器和平台的负担,但会增加海流对立管的尾迹效应,从而加大落点偏离和最大弯曲应力,因此,浮力块加与不加以及加多少必须综合考虑和优化;
5) 本文的仿真结果与现有实验数据具有很好的一致性,但对更复杂情况,本文设置的载荷偏理想化,有待在实践进一步细化和验证。

