基于元胞自动机理论的变压器经济运行

钱 毅，章文俊

(1.上海送变电工程有限公司，上海 200235；2.上海工程技术大学，上海 201620)

变压器的经济运行是电力网运行的一项重要节能措施。至今已有很多文献对该问题进行了广泛深入的探讨[1]。在变压器经济运行理论的基础上，有文献利用遗传算法[2]、基于禁忌搜索算法[3]、时段控制法等进行了诸多研究，还有结合可靠性成本进行了研究[4]等，都取得了一些成果。

本文使用负荷预测数据计算并描绘变压器在各种运行模式下的功率损耗曲线。这些功率损耗曲线之间会产生很多交点。经过简化，只有一些重要的交点被保留，这些被保留的交点对应着变压器运行模式切换的候选时间点。由这些时间点将某个运行日划分为若干个时间区段。根据这些时间区段构造了一种一维不规则元胞自动机(Cellular Automaton, 简称CA)[5-7]，建立元胞自动机转换规则。根据所建立的转换规则，在每个时间区段及其相邻时间区段内变压器产生的能耗都被用于确定相应时间区段内的变压器运行模式，从而可得到变压器在各时间区段内的优化运行模式，在这些运行模式中变压器的优化投切次数也被考虑进来以减少开关设备的机械磨损，当然更重要的是可以降低误动作的可能性。

1 元胞自动机简介

元胞自动机是n维空间内的一些有限状态机[5]，一个元胞自动机由若干元胞组成，这些元胞按照一些简单规则进行迭代演化[8]。CA的基本思想不是去用复杂的数学等式描述一个复杂系统，而是用遵守一些简单规则的元胞之间的相互作用来模拟这个系统。CA模型不是一个确定的数理方程，而是一种方法框架。不同领域的专家可以根据其专题要求对CA模型进行扩展。在实际应用中，许多元胞自动机模型并不是标准的元胞自动机，而是根据具体实际的需要对其中的某个或者说是几个特征进行适当的扩展。如：连续CA及不规则CA就分别被应用于文献[9]和文献[10]中确定邻域形态与影响范围和解决大型超市疏散过程的问题。

此外，基于各种统计方法，文献[11]定义了6类一维CA的情形：①空间均匀固定点；②空间不均匀固定点；③周期行为或移动周期行为；④局部混沌行为；⑤混沌行为；⑥复杂行为。另外，对于大多数CA，一旦CA规则给定，虽然初始条件可能变化，但演化特性通常不会变化。

本文中构造了一种第2类一维不规则CA，且建立了CA规则以优化变压器运行。经过有限步迭代，所构造的CA在各种初始条件下将达到相应的稳定状态。之后，从元胞的状态可获得变压器在各时段的优化运行模式信息。

2 元胞自动机的网格结构

以某变电站两台双绕组变压器为例，技术参数分别为UAk=7.44，UBk=7.39，IA0%=0.45，IB0%=0.38，PAo=8.22 kW，PBo=5.495 kW，PAk=39.507 kW，PBk=33.881 kW，取无功经济当量k=0.1。变压器在各种运行方式下的功率损耗及其变换如图1所示。由该变电站某日预测负荷曲线可计算得到变压器A，B及AB并列运行方式下的日损耗曲线如图1(a)所示，横轴为时间轴(16 min)，纵轴为损耗值(kW)。

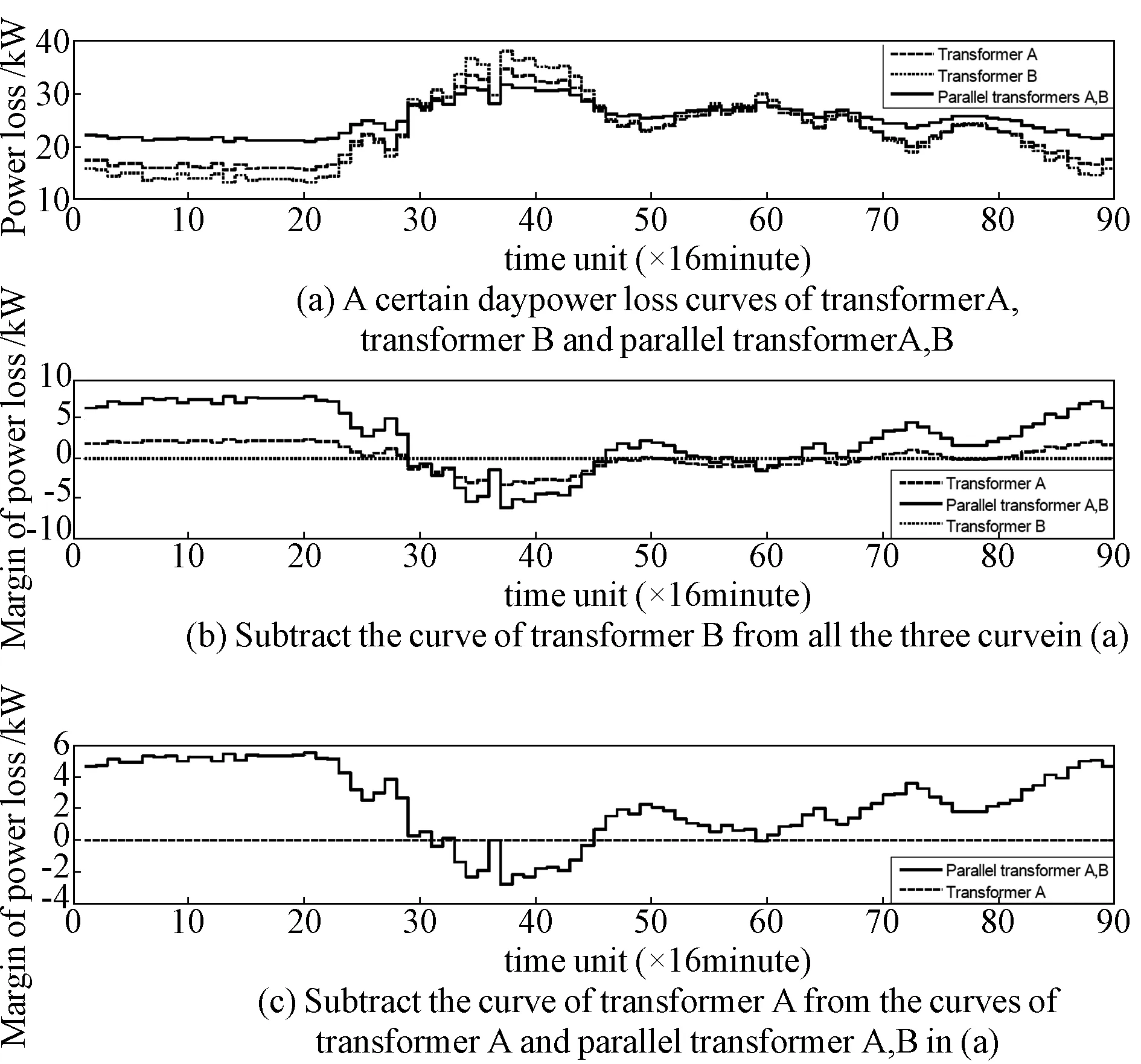
图1 变压器在各种运行方式下的功率损耗及其变换

从图1中可见，由于各种运行方式下综合功率损耗随负载变化而发生非线性变化的幅度各不相同，使得各损耗曲线之间有多个交点。这些交点将一整天分为了很多长短不一的时间段，而由这些时间分段则可获得本文中CA的网格结构。

为了获得CA的网格结构，对图1(a)中损耗曲线稍作变换。m-1(m为变压器运行模式的数量, 本例中m=3)条曲线分别被随机选作基线。首先，以变压器B的日损耗曲线为基线，所有运行方式的日损耗曲线减去该基线，得到图1(b)。同法，以变压器A的日损耗曲线为基线，变压器A及AB并列运行的损耗曲线减去该基线，得到图1(c)。图1(b)中基线与变压器AB并列运行曲线所围面积代数值，正负或负正变号点即为可能的运行方式切换点，这些变号点将一天分为若干时段。当某时区面积代数值的绝对值小于一给定阈值，可设之为零并将该时区并入左侧时区。若某时区面积被设为零，且其两侧面积同号，则把该三个时区合并为一个时区。从而将一天时间的分区简化，并得到一组将一天时间分为若干区段的节点。图1(b)中基线与变压器A曲线、图1(c)中基线与变压器AB并列运行曲线所围面积也是如此处理。

这样，一天时间就可得到三组时间分段节点。这些节点是变压器运行方式切换的备选时间点。本例中这三组时间点将一天时间分为10个时间段。一个时间段对应一个时间元胞，而元胞的长度互不相同，这与传统CA有所不同。从而，就可得到一个具有周期边界条件的元胞自动机，其周期为10个元胞。

3 CA的状态空间及邻居

对于2台双绕组变压器，在一个时间段内通常有3种运行模式：①变压器A单独运行；②变压器B单独运行；③变压器AB并列运行。从而，对于2台变压器而言，一个时间元胞就有3种状态。当然，如有更多变压器，一个时间元胞的状态数将大于3。3种运行模式在10个时间元胞内的能量损耗值如表1所示。

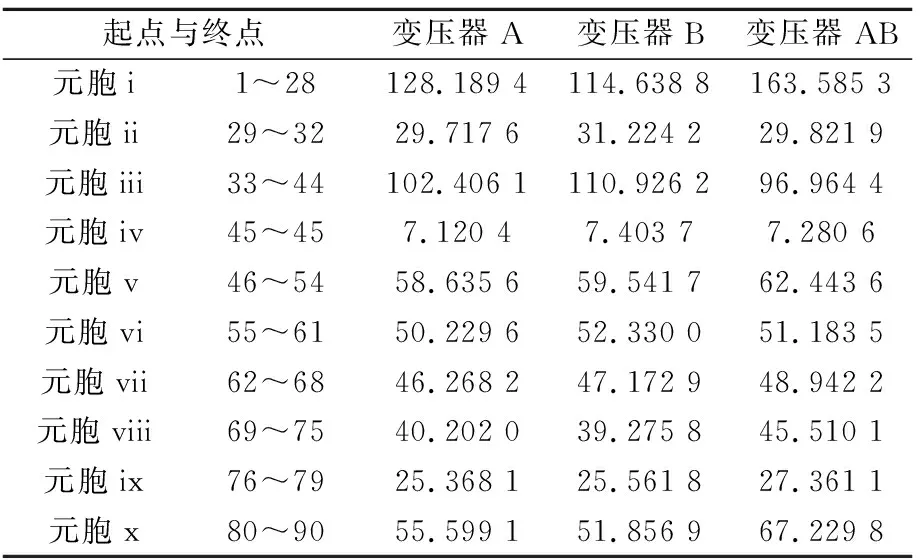
表1 3种运行模式在10个时间元胞内的能量损耗值 kWh

本文中一个时间单位为16 min。作为示例，负荷曲线数据从SCADA系统的历史数据中获得，其采样时间间隔为2 min(为简化处理被乘以8)。表1所示为10个时间元胞对应各种运行模式下的能耗。可对这些数据规格化，可得到所有元胞的初始状态矩阵：

在R0中，每行对应于一个元胞，而元胞所处的状态由矩阵中的数值1所在位置指示出来。若某元胞的头或尾距离某中心元胞不超过15个时间单位，被称为是该中心元胞的邻居，元胞i-1,i+1及i都是元胞的邻居。

4 CA转换规则

变压器的运行中需要考虑2个因素：①能耗应该越小越好。这意味着每个时间元胞应该保持对应于能耗最小的状态；②开关动作次数应该越少越好。这意味着邻居时间元胞的状态应该考虑进来以确定每个元胞的最终状态。

当一个时间段越短，该时间段内变压器的运行模式就更应该由开关动作次数的因素来确定；相反，若一个时间段越长，该时间段内变压器的运行模式就更应该由能耗因素来确定；另外，在实际运行中，一些操作人员会要求两次开关操作的时间间隔不得少于4 h(本文中为15个时间单位)。

为建立元胞自动机规则，本文中提出如下假设：①时间元胞越短，它对邻居的影响就越弱，且其下一步的状态受其邻居的影响就越大。这样更便于其状态与邻居保持一致，从而减少开关设备的操作次数；②时间元胞越长，它对邻居的影响就越强，且其下一步的状态受其邻居的影响也越小。尤其是，如果一个元胞的长度超过15个时间单位，其下一步的状态将只由其当前的自身状态决定，而不考虑其所受邻居的影响，也即邻居对其影响为零。

CA的基本计算流程如图2所示。根据图2中的规则I 至规则IV进行迭代计算，但Rk中数值1的位置已不再改变，而除数值1以外的其他数值将保持在0或者逐渐减少到某个固定数值。也就是说元胞自动机将逐步达到一个稳定状态。

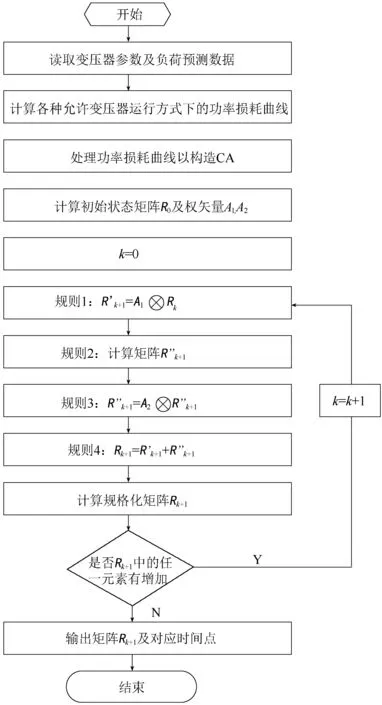
图2 元胞自动机迭代流程

矩阵R1中数值1所在的列数就对应着所应该采用的变压器的运行模式。根据矩阵R1及表1，可得到如下结果：在第1～28时间单位(00:00-07:28)，应该采用第2种运行模式，即单台变压器B运行；在第29～44时间单位(07:29-11:44)，应该采用第3种运行模式，即变压器AB并列运行；在第45～69单位时间(11:45-18:24)，应该采用第1种运行模式，即单台变压器A运行；在第70～90单位时间(18:25-24:00)，应该采用第2种运行模式，即单台变压器B运行。

6种不同变压器运行方法下变压器的能耗及投切次数的比较如表2所示。由表2可知，方法3的能耗在6种方法中是最低的；方法1的能耗比方法3更大，主要是因为一个比较大的导致变压器的投切时间点有错误；方法2在前3种方法中的能耗最大，主要是因为负荷的变化信息没有被充分利用。当然后3种方法的能耗要比前3种都更大。而第6种运行方法是所有6种变压器运行方法中损耗最大的。

表2 6种不同运行方法的能耗及变压器投切次数比较

另外，方法1中虽然采用了容量裕度以避免频繁的开关操作，但结果却不令人满意。方法1的开关投切次数在6种运行方法中最大，这意味着比其他运行方法更多的开关维护工作。

从分析可知，本文所提的方法3在6种运行方法中是最佳选择。

5 测试算例

图2所示的功率损耗曲线是一种典型日负荷的情况，但在实际运行中的日负荷情况却是各种各样的。为了证明本文所提方法的优越性，对不同负荷数据及不同变压器参数的情形进行了很多测试。结果显示本文所提方法确实有效。本文选择了两个与图2负荷情况不同的测试案例进行说明。

5.1 案例I

案例I仍然是两台双绕组变压器。变压器某日功率损耗曲线及其转换如图3所示。案例I是负荷波动比较剧烈的一种情况。案例I中20个元胞在3种运行模式下的能耗值如表3所示。案例I中6种不同运行方法的能耗及变压器投切次数比较如表4所示。

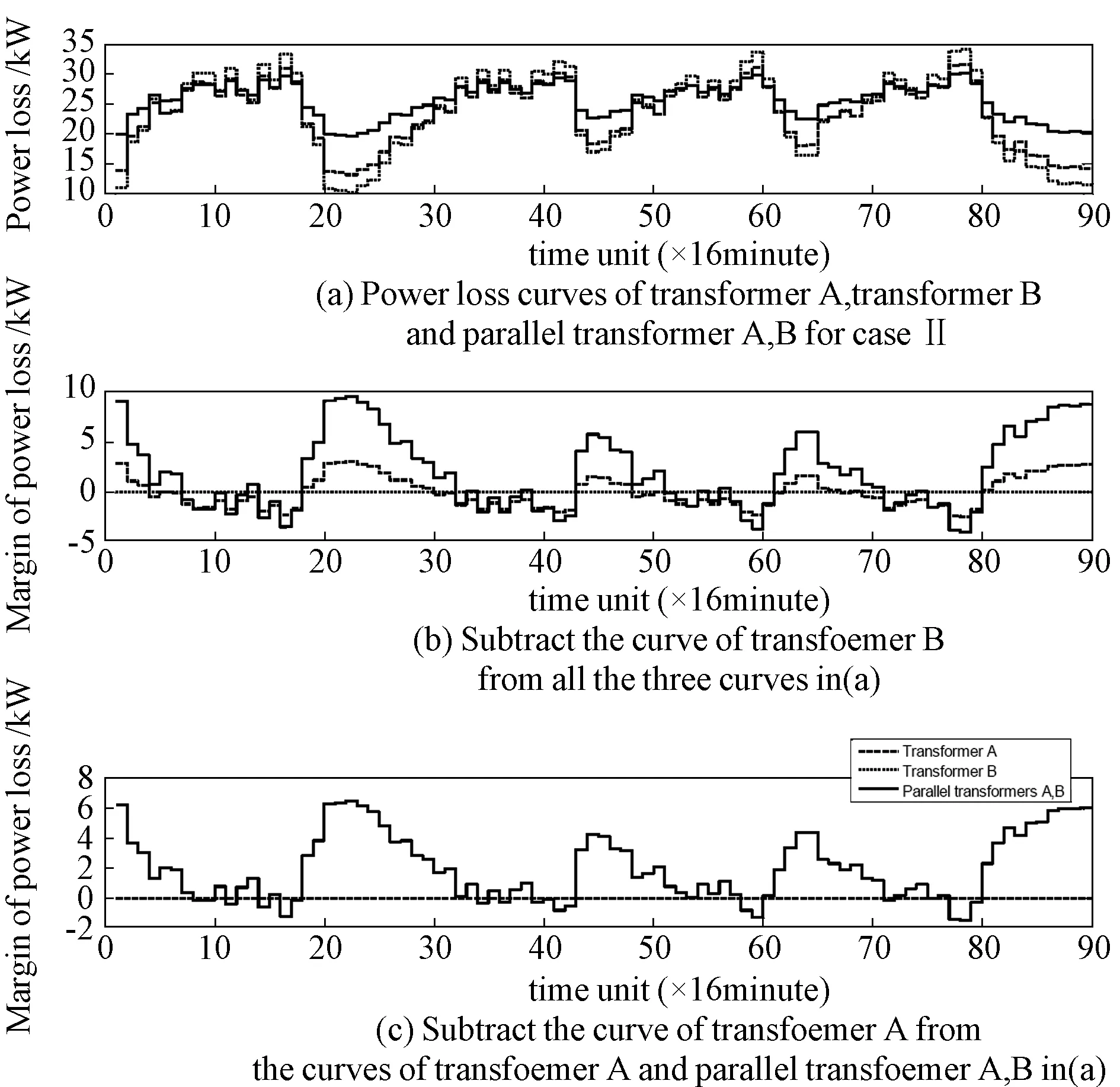
图3 案例I中日功率损耗曲线及其转换

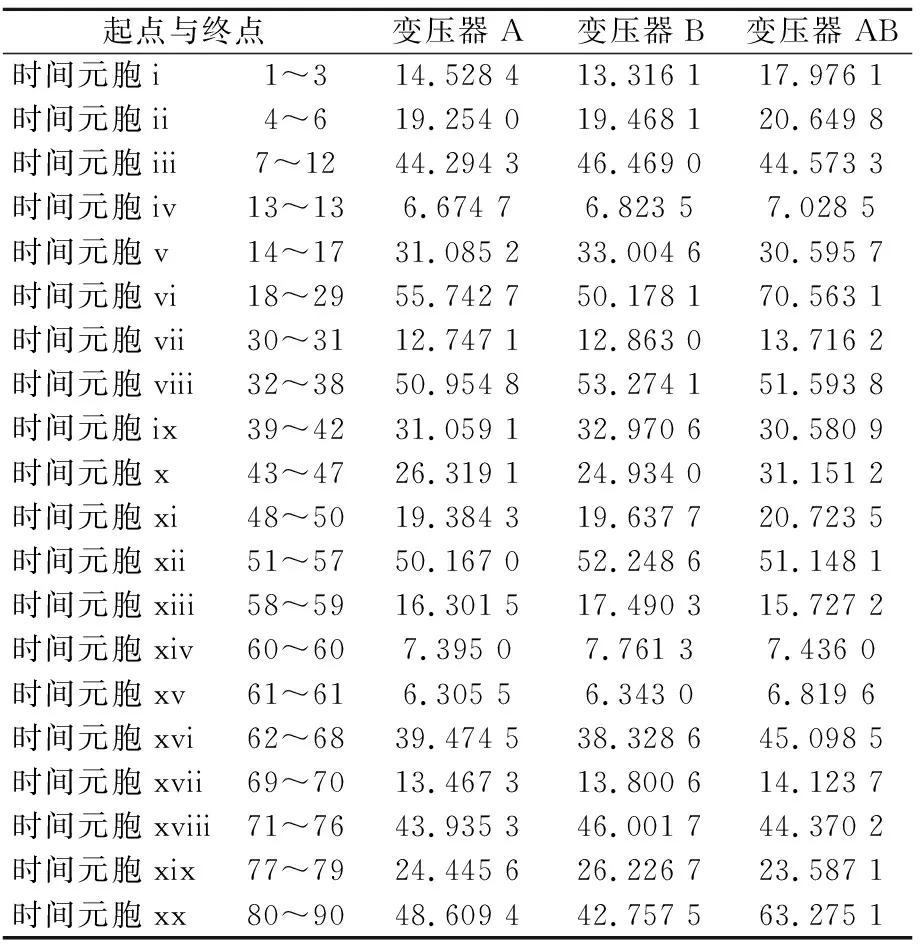
表3 案例I中20个元胞在3种运行模式下的能耗值 kWh

表4 案例I中6种不同运行方法的能耗及变压器投切次数比较

表4为20个时间元胞在3种运行模式下的能耗数据，对这些数据进行处理，可得到初始状态矩阵R0。

根据规则I -IV进行迭代计算，经过6次迭代后可得规格化矩阵R6：

在本案例中，经过6次迭代获得R6后，Rk各行中数值1的位置不再变化。表4为6种不同变压器运行方法下能耗与开关投切次数的比较，结果显示方法3是6种方法中的最佳选择。

5.2 案例II

案例II中变压器日功率损耗曲线如图4所示。本案例中考虑了3台变压器的情况。33个时间元胞中7种运行模式下的能耗值如表5所示。变压器A和B的参数之前相同，变压器C参数为：SNC=4 000 kVA,UkC=6.85,IoC%=0.77,PoC=5.9 kW,PkC=38.360 kW。

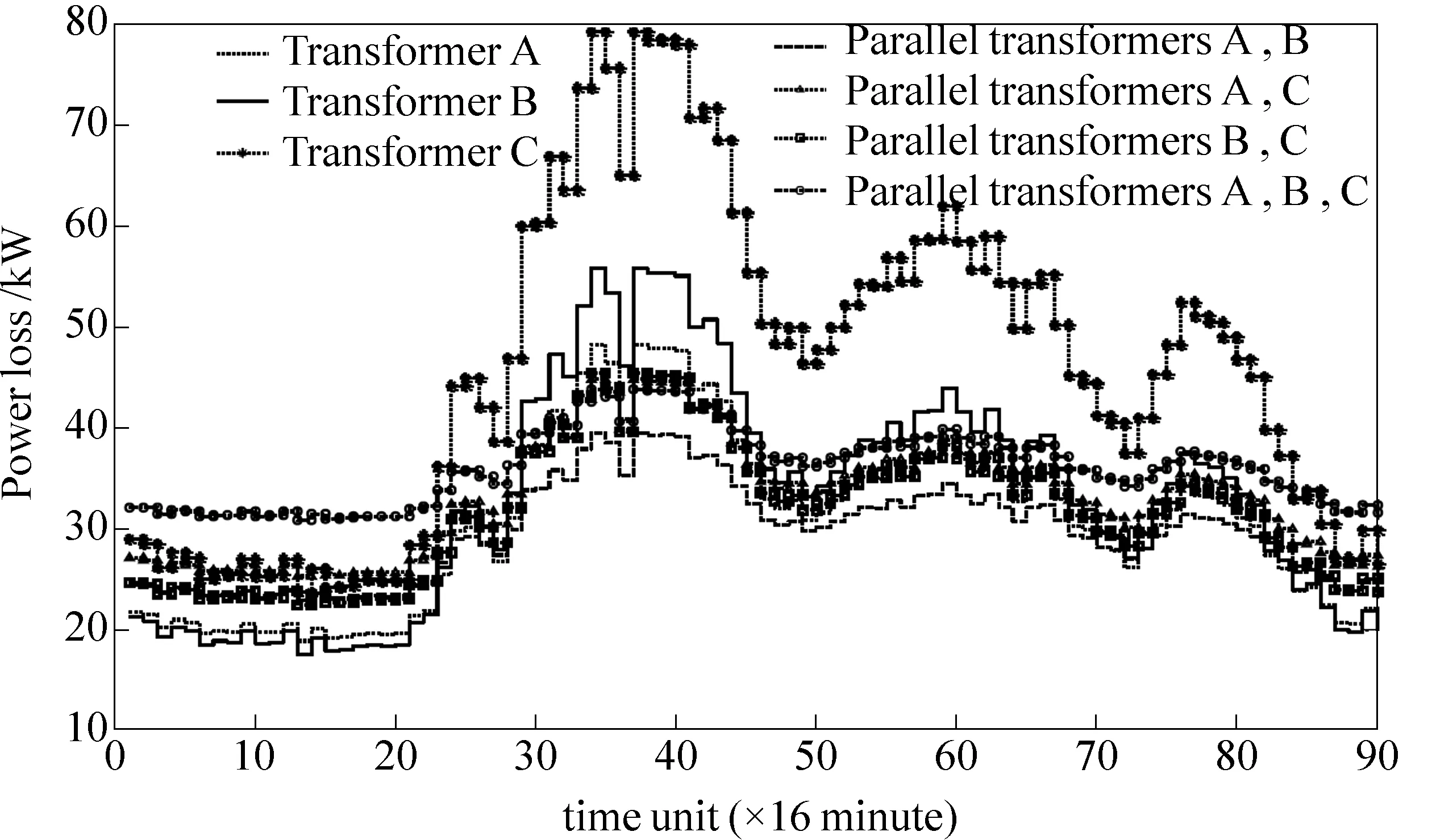
图4 案例II的日功率损耗曲线

根据表5中能耗数据，可计算得到初始状态矩阵R0。再依照规则I-IV迭代，最后得到规格化矩阵R1如下：

表5 案例II中33个元胞在7种运行模式下的能耗值 kWh

在本案例中，经过一次迭代得到R1后，Rk(k≥1)各行中数值1的位置不再变化。从图4及矩阵R1可看出，在大多数时间元胞中都选择的是最低功率损耗的运行方式，但也有一些短时间元胞中选择了次低功率损耗的运行方式，使变压器的投切次数降低到可接受的水平。

总体而言，从各仿真算例及测试算例可见，本文所提方法只用到了各种允许变压器运行模式的功率损耗曲线，且不受变压器的台数及型号(如：双绕组、三绕组或自耦)的限制。所提方法不仅简单方便，而且非常有效。

6 结语

本文构造了一种一维不规则元胞自动机，用于解决变压器的经济运行问题。不同于其他变压器运行决策方法，本方法充分利用了负荷预测曲线的信息，不仅考虑了综合能耗而且能考虑变压器投切次数的因素。该方法不受变压器的台数及型号(如：双绕组、三绕组或自耦)等方面因素的限制，它需要的数据仅仅是变压器在所有允许运行模式下的功率损耗曲线，以及开关设备两次操作之间所允许的时间间隔长度。本方法可高效地做出令人满意的决策，并且方法具有很强的适应性。最后，需要指出的是，虽然元胞自动机方法很有效且计算过程也很简单，但当它被用于执行某种特定的任务时，它的转换规则却是难以设计的。这在某些时候也限制了元胞自动机的推广应用。