基于免疫粒子群算法的宽带雷达目标模拟系统幅频响应校准

李益民，潘明海

(南京航空航天大学，南京 211106)

0 引 言

随着雷达技术的发展，对用于测试雷达系统的实时仿真工具的需求与日俱增[1]。雷达目标模拟系统可以为设计人员提供测试雷达关键功能的机会，并降低开发雷达系统的成本。因此，雷达目标模拟系统广泛用于现代雷达测试和评估[2-3]。随着电子技术的发展，雷达的工作带宽越来越宽。为了准确接收和重构雷达信号，雷达目标模拟系统需要足够的带宽。然而，带宽越宽，信号通带内的纹波越大，系统重构产生的雷达回波信号失真越严重。因此，对系统的幅频响应进行校准，使通带内的幅度平坦是十分必要的[4-7]。目前，采用均衡器的方法被广泛用于校准系统的幅频响应，文献[8-9]介绍了宽带系统均衡器的设计以及用均衡器对毫米波接收前端的幅频响应进行校准，但均衡器只能补偿校准变化平滑的纹波，无法对剧烈抖动的纹波进行精确校准。文献[10]采用IIR滤波器结构设计的数字均衡器来校准系统的幅频响应起到了不错的效果，但IIR滤波器的非线性相位特性会使得系统的群时延波动增大影响系统的性能。文献[11]针对雷达系统利用球形卫星在高速运动中的回波，提出了频域补偿方法，该方法只对平滑的纹波有较好的补偿作用。本文针对宽带雷达目标模拟系统幅频响应通带内剧烈抖动的纹波，采用基于免疫粒子群优化算法设计复杂系数的FIR滤波器，可以精确地对纹波进行补偿，从而降低系统通带内的纹波[12]。

本文算法主要用于补偿和校准由系统本身器件影响使得输出信号产生剧烈变化的纹波。算法首先获得系统输出信号的频谱包络数据，在软件上根据信号的包络设计相应的FIR滤波器，然后用FIR滤波器系数在硬件系统中的DSP或FPGA中设计相应的FIR滤波器。信号经系统ADC采集后由FIR滤波器进行预处理再经DAC输出，从而大大降低了系统本身对信号产生的纹波影响。

1 校准原理

FIR滤波器可用于设计具有任意幅频响应的滤波器，可补偿宽带雷达目标模拟系统通带内的纹波。系统幅频响应的校准问题实际上是FIR滤波器系数的优化问题。FIR滤波器的设计方法很多，如经典频率采样法和Remez逼近法[13]，以及更现代的智能优化算法，如粒子群算法、蚁群算法和免疫算法等[14-16]。传统的FIR设计方法难以设计具有复杂幅频特性的滤波器，而智能优化算法广泛用于设计复杂的FIR滤波器。

粒子群算法是由美国电气工程师Eberhart 和社会心理学家Kenndy 根据鸟类的觅食行为提出的。该算法实现方便，收敛速度快，参数设置少，全局搜索能力强，是一种快速搜索算法。但是经典的粒子群算法缺乏局部搜索能力，而免疫算法通过增加免疫算子可以有效地防止种群退化，从而保持种群的多样性，具有较强的局部搜索能力。本文研究的免疫粒子群优化算法结合了两种智能算法的优点，使算法不仅保证了全局搜索能力，而且提高了局部搜索能力[17-18]。免疫粒子群优化算法的基本原理是使用一个逻辑映射初始化一组粒子，其中每个粒子代表一个随机解，并通过迭代找到最优解。在每次迭代期间，粒子通过跟踪两个极值来更新自身： 一个是粒子本身找到的最优解，另一个是当前整个群体找到的最优解。此外，如果在几次迭代后全局最优解没有明显改善，则产生免疫记忆粒子以更新需要被免疫替代的粒子[19]。

本文研究频率范围为0.1～1.1 GHz的宽带雷达目标仿真系统的幅频响应校准。图1所示为雷达目标模拟系统的幅频响应测试框图。该系统捕获由信号源产生的1 GHz带宽LFM信号，并使用频谱分析仪分析重建信号的幅频特性。工业控制计算机从频谱分析仪获得信号频谱的包络数据，根据信号频谱包络的纹波，采用免疫粒子群优化算法设计FIR滤波器来补偿纹波，使滤波后的信号幅频响应平坦。通过算法获得FIR滤波器系数后，将滤波器系数生成一个.coe文件，用于系统的FPGA中实现FIR滤波器[20-21]。

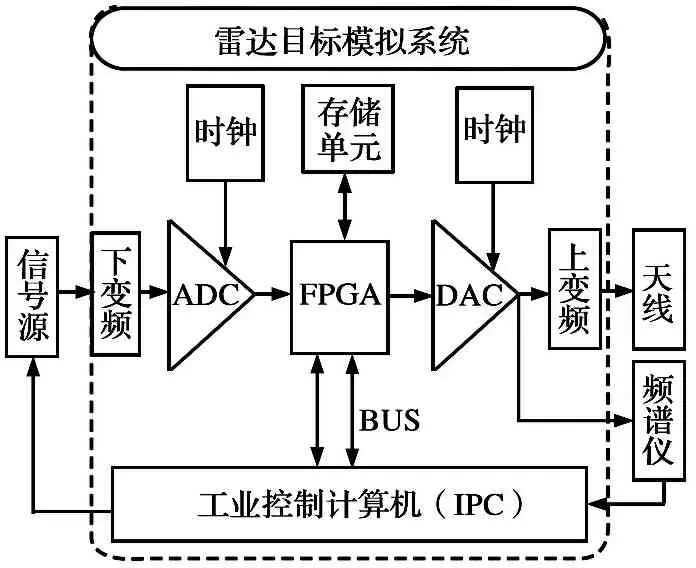
图1 雷达目标模拟系统的幅频响应测试框图

2 校准模型

信号源产生一个理想的0.1～1.1 GHz线性调频信号，根据图1接入系统，通过频谱仪观测系统重构输出信号频谱。图2所示为频谱仪显示的经系统重构输出信号的幅频响应。将频谱分析仪中的信号频谱数据输出到工业控制计算机，通过MATLAB分析数据得到信号通带中幅频响应的包络。图3为系统输出信号通带内幅频响应的包络。

从图2～3可以看出，系统的幅频响应在通带中纹波剧烈，最大幅度波动接近10 dB。

图2 系统重构输出信号幅频响应

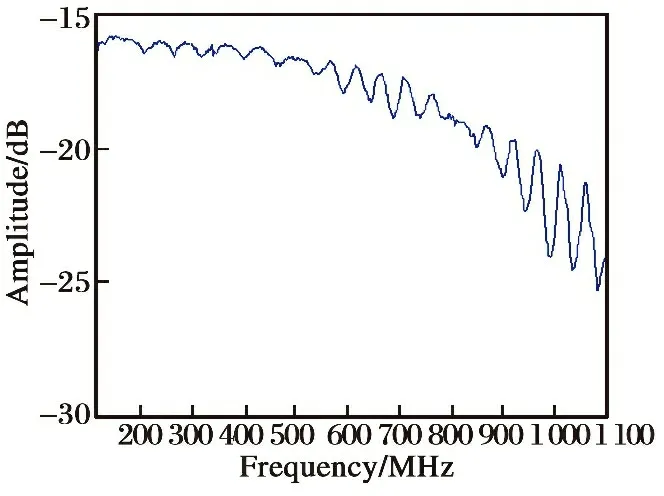
图3 系统输出信号通带内幅频响应包络

频谱仪中的频谱数据可以表示为

X(k)=|X(k)|exp(θ(k))k=1, 2, …,L

(1)

式中：L是频率数；|X(k)|是幅频响应函数。

通带中的幅频响应可以表示为

|Xp(k)|=|X(k)|k=ks, …,kg

(2)

式中：ks是通带中的起始频率；kg是通带中的截止频率。

采用m阶FIR滤波器对幅频响应进行校准。滤波器的系统函数可以写为

(3)

式中：h(n)是滤波器的系数序列； 令z=exp(jω)，滤波器的频率响应函数可以写成

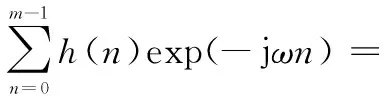
|H(ejω)|exp(φ(ω))

(4)

式中： |H(ejω)|是滤波器的幅频响应函数。若H(ejω)以0到2π之间的相等间隔进行L点采样，则H(k)为

(5)

那么，通带内的幅频响应可以表示为

|Hp(k)|=|H(k)|k=ks, …,kg

(6)

将雷达目标模拟系统和滤波器作为一个整体系统，校准的目的是使系统的幅度响应平坦。理想滤波器的幅度响应需满足:

|Hp(k)Xp(k)|=Ck=ks, …,kg

(7)

式中：C是常数。设计一个理想滤波器是非常困难的，可以等效为优化h(n)问题，使|Hp(k)Xp(k)|的标准差最小：

minimise std(|Hp(k)Xp(k)|)

(8)

3 算法实现

3.1 算法流程

免疫粒子群优化算法优化系数的具体步骤如下：

步骤1： 初始化： 定义粒子的位置。式(4)中的变量是h(n)，则粒子的位置矢量可以表示为

x=(h(0),h(1), …,h(M))

(9)

粒子的速度矢量为

v=(v(0),v(1), …,v(M))

(10)

此外，需设置以下参数： 粒子数目N； 最大迭代次数MAX； 学习因子c1,c2； 随机因子r1,r2； 最大惯性权重w_max； 最小惯性权重w_min； 免疫阈值Th； 粒子间最小间距min_d； 免疫替换概率p； 查询最优粒子时间间隔T。

步骤2： 生成初始种群并计算每个粒子的适应度。适应度函数可以表示为

fitness=std(|Hp(k)Xp(k)|)

(11)

步骤3： 将每个粒子的当前位置适应度与历史最佳位置适应度进行比较。如果当前位置适应度更好，则更新粒子的个体极值，否则不更新。

步骤4： 将每个粒子的当前位置适应度与全局最优位置适应度进行比较。如果当前位置适应度更好，则更新全局极值，否则不更新。

步骤5： 更新每个粒子的位置和速度：

xi, j(t+1)=xi, j(t)+vi, j(t+1)

(12)

式中：i=1, …N；j=1, …,M。

vi, j(t+1)=w·vi, j(t)+c1r1(pi, j-vi, j(t))+

c2r2(pg, j-xi, j(t))

(13)

式中：t是当前迭代次数；pi, j是粒子自身的极值；pg, j是全局极值。

步骤6： 更新惯性权重：

式中：t=1, 2, …,MAX。

(14)

步骤7： 每隔时间T检查全局极值是否显著改善。满足式(15)，转到步骤7.1开始免疫； 否则，转到步骤2。

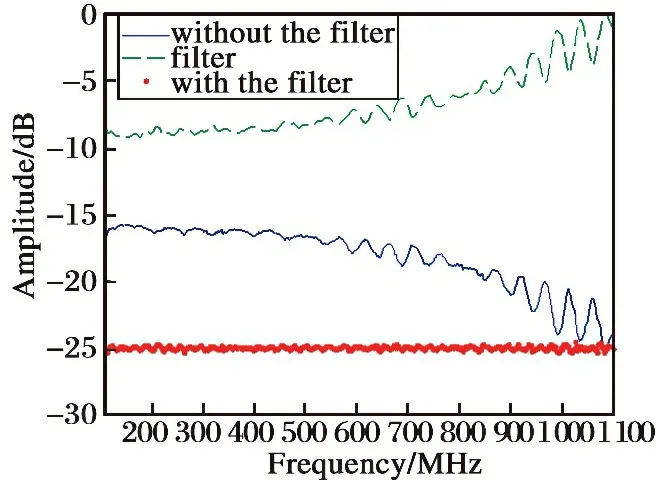
pg(t-T+1)-pg(t)

(15)

步骤7.1： 计算粒子适应度的概率值：

(16)

步骤7.2： 计算与当前粒子的距离小于min_d的粒子数，表示为num，粒子之间的距离表示为

d(i)=abs(p(j)-p(i))

(17)

那么，粒子的个体浓度可以表示为

pd(i)=num/N

(18)

步骤7.3： 计算粒子被免疫替换的概率：

pr(i)=rand*pf(i)+(1-rand)*pd(i)

(19)

式中：v是均匀分布在0和1之间的随机数。

步骤7.4： 若pr(i)>p，按照式(20)替换粒子，否则到步骤5。

xnew(i)=pr(i)*x(i)+(1-pr(i))*pg

(20)

步骤8： 若满足最大迭代次数，则转到步骤2； 否则，转到步骤9。

步骤9： 寻找群体中的最优粒子作为解，终止算法。

3.2 算法计算时间复杂度分析

对本文提出的免疫粒子群优化算法的计算时间复杂度进行理论分析。假设对于m阶FIR滤波器，粒子的数目为n，算法满足收敛条件所需要的迭代次数为M(m,n)。对于免疫粒子群优化算法一个粒子更新一次，需要进行7次加法与7次乘法运算。如果每隔T次检查粒子需要进行免疫处理，则一个粒子免疫处理一次需要n+4次加法与5次乘法，需要免疫的概率与免疫阈值有关，设为P(r)，假设一次乘法运算的时间为tm，加法运算的时间为ta，则免疫粒子群优化算法完成m阶FIR滤波器优化设计所需要的时间t为

(5tm+(n+4)ta)

(21)

4 实验仿真

4.1 仿真分析

采用免疫粒子群优化算法设计了不同阶的FIR滤波器，并比较了不同阶数的FIR滤波器对系统幅频响应的补偿效果。由于免疫粒子群优化算法的参数对优化结果有影响，因此对其进行了细致的设置。考虑到问题的复杂性，免疫粒子群优化算法的参数设置如下： 种群大小N=256； 最大迭代次数MAX=500； 学习因子c1=2,c2=2.5； 最大惯性权重w_max=0.8； 最小惯性权重w_min=0.8； 免疫阈值Th=0.1； 粒子间最小间距min_d=0.1； 免疫替换概率p=0.2； 查询最优粒子时间间隔T=10。

图4所示为采用免疫粒子群优化算法设计的不同阶数FIR滤波器对系统的幅频响应补偿校准后通带内的纹波。由图可知，FIR滤波器的性能随着滤波器阶数的增加而提高。然而，当滤波器的阶数大于64阶时，滤波器的性能没有显著提高，而且阶数越高，算法需要迭代的次数会显著增加，需要的时间也会成倍增长，在FPGA中也需要使用更多的硬件资源。图5所示为64阶FIR滤波器幅频响应、未使用滤波器进行校准和使用了FIR滤波器进行补偿校准的信号幅频响应。由图可知，在使用FIR滤波器校准后，系统的幅频响应得到了显著改善，使得系统输出信号通带内幅频响应在1 dB以内。

图4 不同阶数滤波器校准后信号纹波

图5 使用与不使用滤波器校准的信号幅频响应比较图

4.2 实验测试

滤波器系数是通过免疫粒子群优化算法仿真得到的，但系统实现需要在FPGA中设计滤波器，因此有必要生成.coe文件，并将获得的滤波器系数导入FPGA中设计的FIR滤波器IP核中。系统测试是按照图1所示的系统框图进行实验，通过频谱仪观测加入FIR滤波器之后系统输出信号通带内的幅频响应，并与仿真结果进行比较。图6为分别加入64阶和128阶FIR滤波器校准后的雷达目标仿真系统幅频响应的实验测试结果。

图6 FIR滤波器校准后信号幅频响应

与图2相比，图6在加入FIR滤波器后明显改善了系统输出信号通带内的幅频响应，加入64阶滤波器使得通带内起始频率与终止频率信号的纹波在1 dB左右，加入128阶滤波器信号的纹波在0.5 dB左右，但从整个通带内的平坦度来看，128阶的滤波器并不明显优于64阶滤波器，而且设计128阶滤波器算法所花费的时间是64阶的好几倍，所占用系统硬件FPGA资源也远超过64阶，滤波器阶数的选择与系统纹波变化的剧烈程度有关。对于一般宽带系统，64阶滤波器可以满足需求。

由图6可知，校准之后输出的幅频响应在-25 dB左右，这是因为未校准前信号经系统输出在1.1 GHz处的幅频响为-25 dB左右，算法所设计的FIR滤波器为无源滤波器，因此，校准后系统整个通带内的幅频响应在-25 dB左右。系统幅频响应的降低会使系统的无杂散动态范围减小，对系统性能有一定影响，后续将研究采用加入有源均衡器进行粗校准，再采用FIR滤波器进行精校准，在降低系统纹波的同时提高系统的幅频响应。

5 结 论

本文采用免疫粒子群优化算法，设计了用于校准雷达目标模拟系统通带内幅频响应的FIR滤波器。设计的FIR滤波器和适应度函数有效补偿了通带中的幅度变化。免疫粒子群优化算法避免了粒子群算法中的早熟收敛问题，并增强了局部搜索能力。从实验和仿真结果可以证明，采用免疫粒子群优化算法设计的FIR滤波器对信号进行校准后，信号通带内幅频响应的纹波小于1 dB。采用该方法可以显著提高雷达目标模拟系统的幅频响应，从而有效减小系统重构信号的失真。