机动发射导弹对空间平台快速支援发射窗口分析

魏鹏涛，肖 勇，龙 霞

(火箭军指挥学院，武汉 430012)

0 引 言

随着战争形态的发展，控制并利用空间成为推动战争天平向己方倾斜的重要砝码。在未来战争中，利用空间作战平台从太空对敌方进行攻击成为各国竞相追逐的一种新的作战方式，该方式具有攻击速度快、对目标毁伤强、突破敌防御系统好的优势[1-4]。但是由于空间作战平台距地面距离较远，对其支援保障困难，严重影响了其持续作战能力。对于空间平台的快速支援问题，目前主要依托位置相对固定的火箭进行投送支援的方式。该支援方式由于发射点位置较少且相对固定，战时对于空间紧急投送支援任务，通常需要等待较长时间才能获得发射窗口，受限制条件多，难以满足作战快速性、实时性要求[5-8]。如果采用机动发射的方式，则可以通过改变发射点的大地坐标来获得需要的发射窗口，且该方式可以发挥发射点的选择优势，在战时紧急情况下优势明显。因此，可以将机动发射的导弹作为运载工具，从而有效发挥其数量较多、机动性好、性能稳定的优势，能较好地完成对空间平台的快速支援任务。

1 发射窗口问题描述

在未来战争中，对于在空间作战中具有优势的一方而言，如何有效发挥空间作战平台的作战优势成为其迫切需要解决的问题。战时只有对空间作战平台进行武器的快速补充支援，才能使其始终保持作战能力，进而发挥其独特优势。但是，从地面对空间作战平台进行快速支援时，发射窗口的选择往往受诸多因素限制，如地面发射场的位置、发射时的天气条件以及空间平台的空间运行情况等。将机动发射的导弹作为运载平台，则可以对空间平台进行快速支援，其发射窗口的选择便显得异常重要，因此，本文将其作为研究的重点问题。利用机动发射的导弹进行空间快速投送支援时所选择的发射窗口涉及两个重要能力： 异面变轨能力和共面调相能力，快速机动发射导弹所具有的这两个能力均与发射窗口密切相关。本文假设从地面某点某时间段机动发射的导弹在飞行过程中通过适当的机动控制，最终进入空间之后其轨道平面能够与空间平台运行的轨道面重合，则该时间段为机动发射导弹的平面窗口； 假设从地面某点某时间段机动发射的导弹进入空间平台运行轨道后的位置，与空间平台的瞬时位置之间的相位差处于导弹能够进行空间机动调节的范围之内，从而实现机动发射的导弹在空间预定的时间位置对空间平台进行支援，则该时间段为相位窗口[9-10]。

机动发射导弹发射后飞行轨道面内相关角度关系如图1所示，其中：B为标称入轨点；P为发射点； Δθ0为标称入轨相位差； ΔθG为共面调相能力； Δθk为入轨精度偏差；φa为可到达相位的下限；φb为可到达相位的上限；OE为地心。

假设机动发射导弹发射时与空间平台的非共面夹角限制为Δi，任意时刻发射点地心矢量与空间平台轨道平面的夹角为Δθ(t)，则机动发射导弹发射的平面窗口应为[t1,t2]，且有

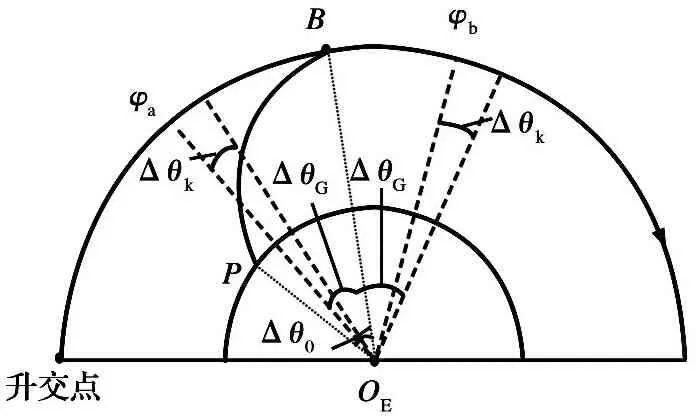
图1 轨道面内各相关角度关系示意图

Δθ(t1)=Δi

(1)

Δθ(t2)=Δi

(2)

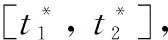
(3)

(4)

要实现机动发射导弹对空间平台的快速支援，其发射时刻必须同时满足平面窗口条件和相位窗口条件。假设最终得到的发射窗口为[ta,tb]，则

(5)

2 机动发射窗口模型

2.1 平面窗口模型

假设t0为机动发射导弹发射时的初始时刻，在t0时刻空间平台的轨道根数为a(t0)，e(t0)，i(t0)，Ω(t0)，ω(t0)，f(t0)； (L,B,H)为发射点P的大地经纬高坐标(采用地心经纬度定义)； Δi为机动发射导弹的非共面发射夹角限制(即导弹发射轨道平面与空间平台轨道平面的最大夹角限制)。

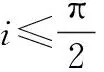
平面窗口的两端点时刻t1,t2及共面时刻tg可表述如下:

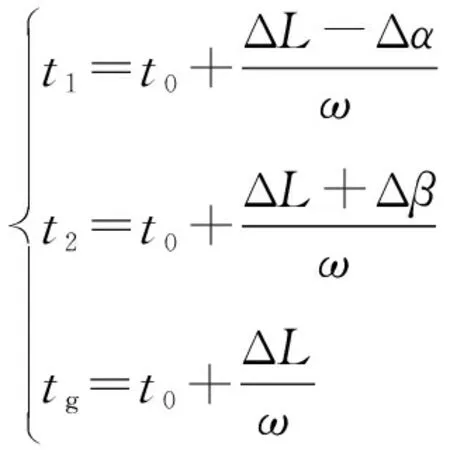
(6)

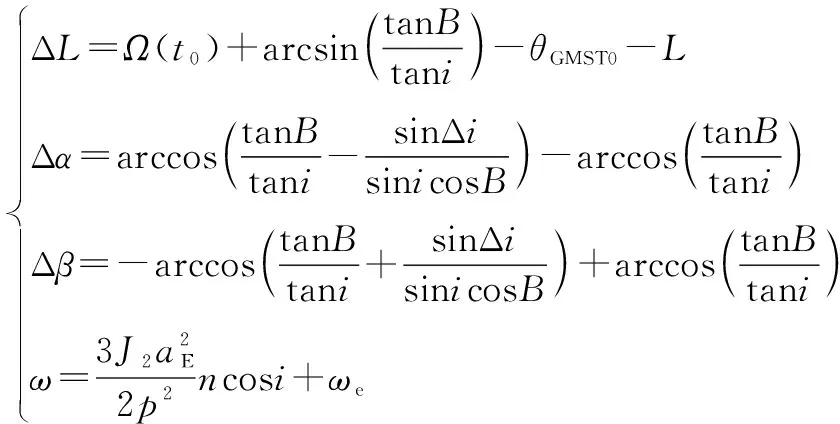
(7)

(8)

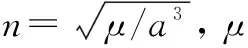
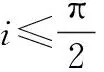
平面窗口的两端点时刻t1，t2和平面窗口的中间时刻tm为

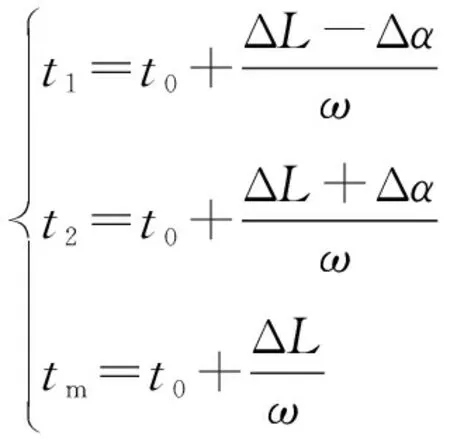
(9)

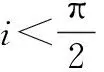
(10)

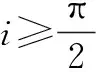
(11)

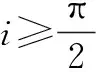
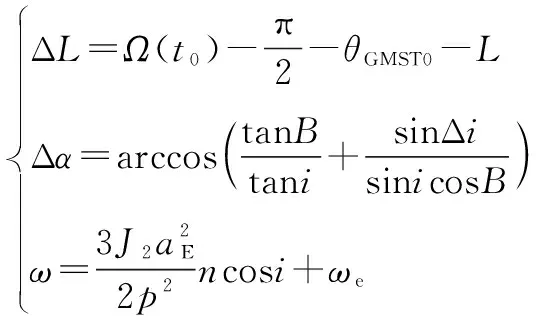
(12)

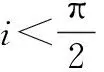
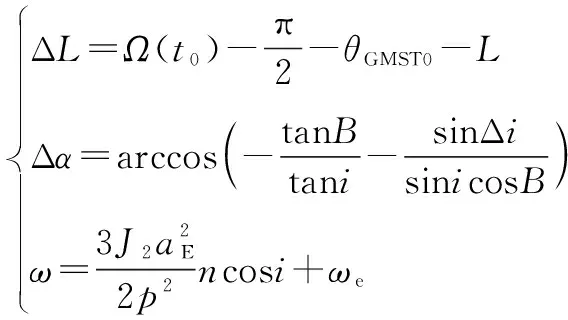
(13)

2.2 相位窗口模型

对于机动发射导弹初始发射时刻与空间平台的相位窗口关系，可用空间平台和机动发射导弹发射点的纬度幅角差来进行描述。对于空间平台来说，任意时刻t时，其总纬度幅角ψ(t)可表述为

ψ(t)=ψ0(t)+2πN

(14)

式中：ψ(t)为当前时刻空间平台相对于该时刻其轨道升交点的总相位，ψ(t)∈[0, +∞)；ψ0(t)为空间平台当圈纬度幅角，具体是指当前时刻空间平台相对于该时刻其轨道升交点的当圈运行相位，ψ0(t)∈[0, 2π)；N为空间平台绕地球运行时经过升交点的次数。对于机动发射的导弹而言，任意时刻t时，其发射点的总纬度幅角φ(t)则可以表述为

φ(t)=φ0(t)+2πM

(15)

发射点纬度幅角示意图如图2所示。假设O点为地心；P点为机动发射导弹的发射点；S点为空间平台轨道的升交点；C点为过P点和O点作与空间平台运行轨道垂直的大圆时，空间平台轨道与大圆所产生的交点。假设任意时刻P点对应的总纬度幅角φ(t)为当前时刻C点在空间平台轨道对应的总纬度幅角；φ0(t)为机动发射导弹发射点相应的当圈纬度幅角；M等于C点顺轨经过空间平台轨道升交点的次数减去C点逆轨经过空间平台轨道升交点的次数[11]。

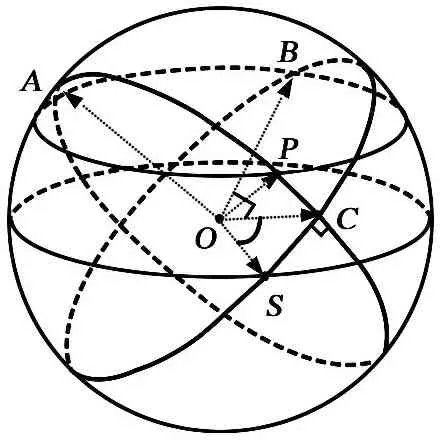
图2 发射点纬度幅角示意图

由于机动发射导弹发射点的标称入轨相位差为Δθ0，因而t时刻空间平台与机动发射导弹发射点的总纬度幅角差为

Δφ(t)=ψ(t)-φ(t)

(16)

将式(16)代入式(14)～(15), 则有

(17)

(18)

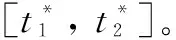
2.3 发射窗口模型

对于机动发射的导弹而言，实现对空间平台的快速支援，必须满足两个条件： 一是不同轨道面的机动条件； 二是同一轨道面不同位置的机动条件。也就是说，机动发射的导弹要实现对空间平台快速支援，其发射时刻必须同时满足平面窗口条件和相位窗口条件，即对于一枚导弹而言，其机动发射窗口为。由于战时机动发射的导弹对空间平台进行投送支援的具体时间无法提前预知，为了保证机动发射的导弹能在任意时刻对空间平台进行快速支援，单靠一台发射车发射一枚导弹进行运载支援往往不能满足战时支援需求，需要多台发射车进行多点同时部署。因此，对于发射窗口的确定问题便不是单发导弹就可解决的，而是需要确定多发导弹的发射窗口。对于多发导弹发射窗口，如果对其进行合理设计，则可以大大提升机动发射导弹对空间平台的支援效率。这里假设机动发射导弹的平面窗口的大小为Δt； 空间平台运行的角速度为n； 机动发射导弹进行共面调相的能力大小为ΔθG； 入轨点的控制精度偏差为Δθk。nΔt为机动发射导弹的异面变轨调整相位的大小，因此，机动发射导弹入轨点相位区间的大小Δφ为

Δφ=ΔθY+2ΔθG-2Δθk=nΔt+2ΔθG-2Δθk

(19)

假定机动发射导弹标称入轨点相位为φ0，从选定发射点发射后一次穿过空间平台轨道平面时间内能够到达空间平台轨道相位的范围[φ1,φ2]，则有

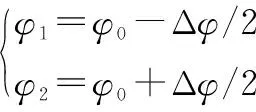
(20)

如果想对空间平台轨道实施全相位快速支援保障，则需要实现机动发射导弹进入空间轨道后，能够从入轨点机动到达空间平台轨道的全部相位位置。因此，机动发射导弹可选择机动发射点的数量N为

(21)

式中： []表示取上限整数。为了实现机动发射导弹对空间平台轨道的全相位位置支援保障，可通过计算得到N个可选择的机动导弹的发射点，对任意相邻两个发射点之间的经度差设置为相等的角度Δσ，并且将发射点分别设置在相应的纬度上，其中，Δσ可表述为

(22)

式中：ωe为地球自转角速度；T为空间平台的轨道运行周期。

3 仿真分析

在本文仿真条件中，假设空间平台在t0时刻的空间轨道根数为：a0=7 068 503 m，e0=0，i0=62.8°，Ω0=39.5°，ω0=0°，M0=0°；t0时刻为2018年1月1日12： 00； 根据机动发射导弹的实际机动变轨能力，将其非共面夹角设置为Δi=3.1°； 将机动发射导弹发射点的坐标设置为(L,B)。通过仿真，计算得到将机动发射导弹发射点的经度设置为L=115°时，不同纬度的发射点的发射窗口情况, 如图3所示。具体发射窗口分布图，如图4所示。

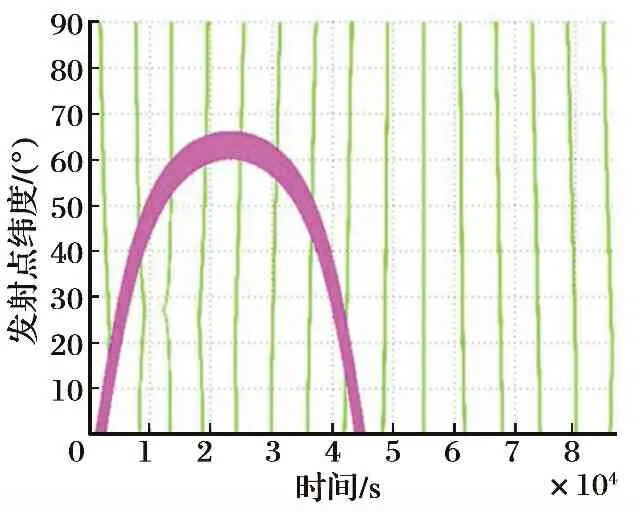
图3 平面窗口与相位窗口叠加情况

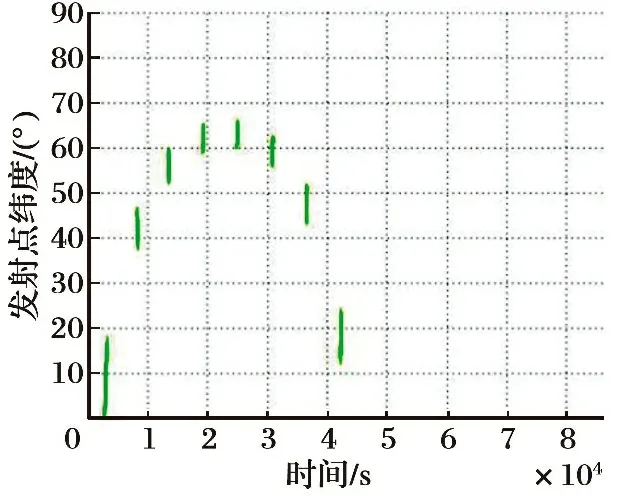
图4 发射窗口

从图3可以看出，如果将机动发射导弹的发射点纬度设置为B=60°时，机动发射导弹平面窗口宽度则出现了跳跃，窗口宽度瞬间增加了一倍。这是由于在发射点B=60°附近时，一天内的两个平面窗口汇合到了一起，使平面窗口的宽度增加了一倍。从图4可以看出，对于将机动发射导弹的发射点纬度设置为北纬40°的发射点时，在24 h内只有一个可用于发射的时间段，即存在1个发射窗口； 而对于北纬60°的发射点，24 h内存在的发射窗口则有3个。表1给出了纬度为40°和60°的两个发射点24 h内的发射窗口情况。

假定机动发射导弹发射点的经度为L=115°，纬度为B=30°，标称入轨点相位为φ0=60°，共面调相能力为ΔθG=10°，控制精度偏差为Δθk=1°。则根据上述条件可求得导弹平面窗口宽度大小为Δt=1 683.8 s，导弹异面调相能力为ΔθY=103.619°，导弹入轨点相位区间大小为Δφ=121.619°，导弹可到达目标轨道相位区间为[φ1,φ2]=[-0.809 5°, 120.809 5°]，从而可求得导弹发射点的最少数量应为N=3，Δσ=8.147 3°，3个发射点经度分别为115°、106.852 7°、98.705 4°，纬度都为30°。表2为机动发射导弹发射窗口的计算结果。从表2可以看出，采用本文方法部署的导弹发射点在24 h内存在2个发射窗口，且当发射点阵第一次穿过空间平台运行轨道平面时，经度为L=98.705 4°的发射点存在发射窗口； 当发射点阵第二次穿过空间平台运行轨道平面时，经度为L=115°的发射点存在发射窗口。

从以上分析可以得出： 机动发射的导弹要实现对空间平台的快速支援，在满足作战地域的条件下，导弹发射点应尽可能部署在较高的纬度，发射点的纬度设置的越高，则导弹发射的平面窗口宽度就越大，从而所需发射点的具体数量就越少； 可将机动发射导弹的发射点部署在与目标轨道面倾角相同的纬度圈上，因为此时一个发射点在短时间内就存在3个发射窗口。

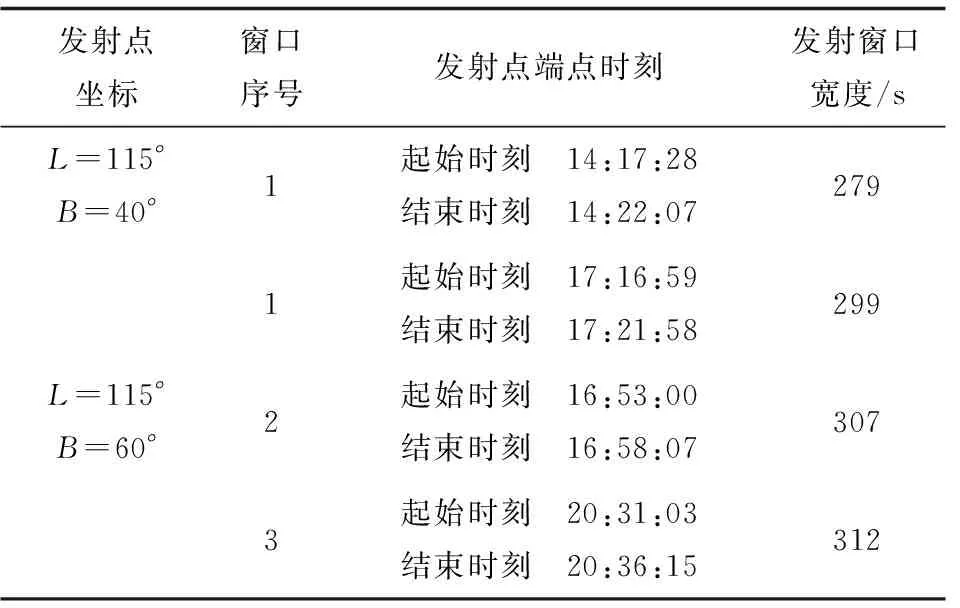
表1 不同纬度发射点发射窗口情况

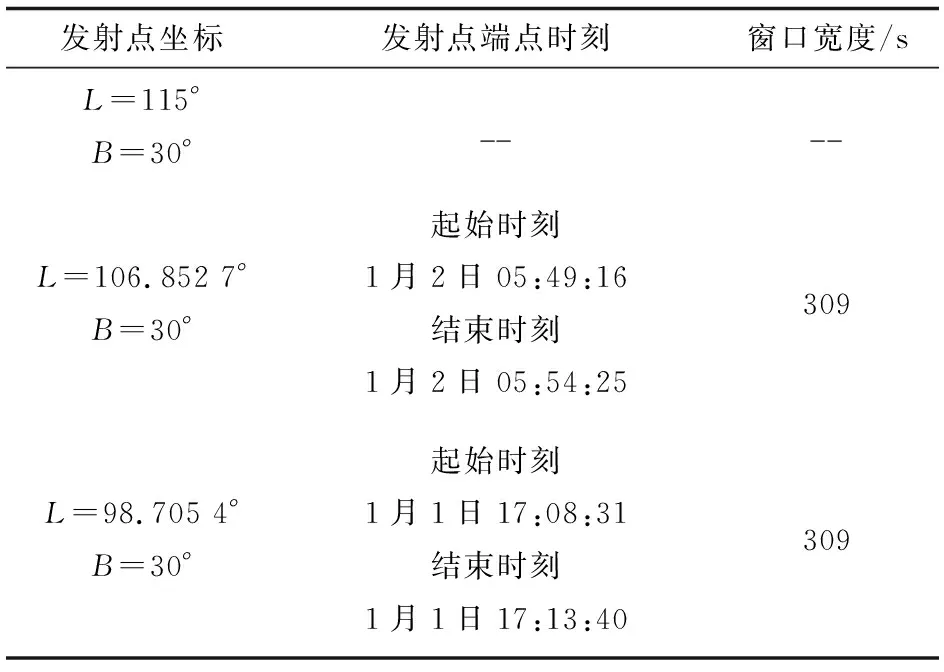
表2 发射点阵的发射窗口

对于上述仿真中采用的空间平台进行快速支援，假设本文采用的导弹发动机参数如表3所示，选择发射点坐标为L=106.852 7°，B=30°，经过数值仿真计算，当发射时刻为2018年1月2日05： 50： 00时，导弹飞行374 s后于2018年1月2日05： 56： 14到达空间平台位置展开支援[12-14]。

4 结 论

利用机动发射的导弹作为运载工具，发挥其数量较

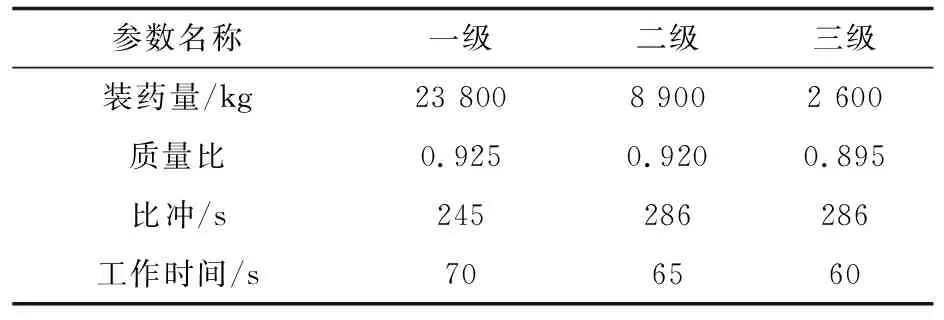
表3 投送火箭发动机性能参数

多、机动性好、性能稳定的优势，可实现对空间作战平台的快速投送支援。本文针对导弹快速投送支援发射窗口选择问题进行了初步研究, 未来作战时，使用机动发射的导弹进行空间快速支援还涉及轨道规划、最优控制、平台对接等多类问题，下一步需要进行更深入的具体研究。