基于向后选择多元回归方法的空空导弹脱靶距离模型研究

常坤龙，高 静，沈 欣, 陈伟衡

(1.中国空空导弹研究院，河南 洛阳 471009； 2.航空制导武器航空科技重点实验室，河南 洛阳 471009; 3.空装驻洛阳地区第一军事代表室，河南 洛阳 471009)

0 引 言

现代战争离不开空中优势的支持，性能先进的空空导弹是夺取和保障空中优势的重要手段，随着超视距空战时代的到来，具有超视距攻击能力的雷达型空空导弹在空战中的作用越来越明显[1-2]。新一代雷达型空空导弹具有全天候使用、全方位攻击、多目标攻击、抗电子干扰等优点[3]。导弹研制过程中，半实物仿真[4]具有成本低廉、试验数据采集全面且与外场数据较为相仿等特点。但仿真试验分析中，数据量庞大且参数繁多，因此，优化数据分析方法，筛选数据参数，就显得迫在眉睫。

空空导弹在末制导段，目标战机面对导弹来袭，往往会采取投放干扰或做规避机动等手段躲避导弹攻击，这可能使雷达制导系统的测量信息出现误差，造成导弹脱靶距离增大甚至导弹脱靶。本文选取末制导段的半实物仿真试验数据，考察典型制导参数回路下，雷达导引头测量参数与脱靶距离[5]之间的关系[6]。利用向后选择的多元回归方法对各项指标进行筛选，得到与脱靶距离显著相关的试验参数，建立了脱靶距离检验模型，并对模型进行有效性验证，实现对半实物仿真平台脱靶距离的检测。同时，利用标准回归系数，对比了筛选后的导引头测量参数，得到了约束量测参数控制侧重点的条件，对比结果与工程经验基本吻合。本文中回归模型的建立和显著性检验方法均由MATLAB软件编程实现。

1 研究方法

1.1 确定多元线性回归研究方法

多元线性回归分析是处理多变量相关关系的一种数量统计方法[7]，用来研究多个变量对因变量的影响程度。该方法通过建立多个变量与因变量之间的统计关系方程式，对未来时刻的量做出估计，有助于认识客观事物的定量关系及内在规律。本文拟采用多元线性回归的方法，建立多元线性回归模型，对脱靶距离与各相关参数进行分析，明确脱靶距离与其自变量之间的相互关系。

由于导弹参数尤其导引头参数均会对脱靶距离产生一定的影响，如果未经显著性检验就将所有的参数考虑在回归模型中，则有可能影响模型精确度，并且降低模型的检测速度。同时，由于不同的自变量组合模型计算出的脱靶距离检测模型也有所差异，而所有模型组合中必有一个检验模型最为精确，因此自变量最优组合的确定对估计脱靶距离至关重要。

向后选择法[8-9]是对包含所有变量的模型进行分析，根据其对因变量的贡献程度逐次剔除对脱靶距离影响不显著的自变量，即当有多个自变量对因变量无显著影响时，由于自变量之间的相互作用，不能一次剔除所有不显著的变量。原则上每次只剔除一个变量，然后再对求得的新方程进行检验，直到保留的变量都有显著性影响为止。与之相对应的前向选择法的思想是变量由少变多，每次增加一个，直至没有可引入的变量为止[8]。若自变量相互独立，前向选择法和向后选择法在选择效果上是相同的。但是在实际情况中，很难碰到自变量之间真正无关的情况，这就会使得随着回归方程中变量的增加和减少，某些自变量对回归方程的影响也会发生变化。如果几个自变量的联合效应对因变量有重要作用，但是单个自变量对因变量的作用都不显著，那么前向选择法就不能引入这几个自变量，而向后选择法却可以保留这几个自变量，因此，本文选用向后选择法对脱靶距离进行分析。

1.2 向后选择法多元回归模型显著性检验

应用向后选择法建立多元回归模型需要进行逐次显著性检验，研究每一步模型的有效性。

首先，为考虑各自变量对脱靶距离的影响，采用显著性检验对所有自变量参数单独进行变量回归系数的显著性分析，并按照回归模型的假设检验方法分析各模型有效性，剔除无效参数； 其次，将满足检验的参数作为多元回归自变量，对脱靶距离建立多元回归模型，并检验该模型的有效性； 再次，若建立的方程有效，则对该多元回归方程中的每个参数进行检验，因为多元线性回归中，回归方程显著并不意味着每个自变量的影响都显著，如果出现多个不显著的参数，则剔除检验概率最低的参数； 最后，利用余下的参数重新建立多元回归模型，重复上一步过程，直到每个参数均显著，即得到向后选择多元回归模型。

1.2.1 自变量的显著性检验

对各个自变量进行显著性分析，保证每个自变量对脱靶距离的影响是显著的。

构造一元回归方程，即

(1)

由最小二乘拟合可知，如果数据的离散程度过大，拟合效果将非常不理想。此时应使用假设检验的F检验法[10]。F检验是根据平方和分解式，直接从回归效果检验回归方程的显著性。检验的原假设为

(2)

平方和分解式为

(3)

SST=SSR+SSE

(4)

据此可以构造F检验统计量为

(5)

在正态假设下，如果原假设H0成立，则因变量Y与自变量Xi之间没有真正的线性关系，F服从(1,n-2)的F分布。当F>Fα(1,n-2)时，拒绝H0，说明回归方程显著，自变量与因变量有显著线性关系。

1.2.2 多元回归模型的显著性检验

多元回归的模型同样利用F检验法。

多元回归模型可以表示为

Y=β0+β1X1+β2X2+…+βpXp+ε

(6)

式中：β0，β1，…，βp为p+1个未知参数；β0为回归常数；β1，…，βp为回归系数；Y为被解释变量(因变量);X1，X2，…，Xp为p个可以精确测量并可控制的一般变量，为解释变量(自变量)；ε为随机误差。

提出原假设：

H0:β0=β1=…=βp=0

(7)

构造F检验统计量如下：

(8)

其他计算步骤与一元回归相似。当F>Fα(p,n-p-1)时，拒绝原假设，认为在显著性水平α下，多元回归方程是显著的。

1.2.3 回归模型中各自变量的显著性检验

由于F检验法是针对多元回归整体模型的检验，需要选用t检验法[11]对各个自变量进行显著性检验。

原假设：

H0j:βj=0j=1,2,…,p

(9)

记：

(X'X)-1=(cij)ij=0,1,2,…,p

(10)

于是有

(11)

(12)

当原假设H0j:βj=0成立时，式(12)构造的tj统计量服从自由度为n-p-1的t分布。给定显著性水平α，查出双侧检验的临界值tα/2。当|tj|≥tα/2时，拒绝原假设H0j:βj=0，认为自变量Xj对因变量Y的线性效果显著，即影响显著。

通过t检验法可以筛选出影响不显著的自变量，并剔除影响最小，即|tj|min对应的自变量，再重复1.2.2和1.2.3操作，直到自变量均满足|tj|≥tα/2为止。

2 回归模型的建立

雷达导引头测量参数众多，本文选取若干具有代表性的参数，建立与脱靶距离的回归模型。

2.1 多元线性回归模型参数的定义

2.1.1 定义多元回归因变量

脱靶距离本质上是一个误差，用来测度威胁系统将战斗部送到飞机附近区域的能力[12]，是导弹性能的基本测量参数[13]。径向脱靶距离是制导导弹和目标在最接近(CPA)处的标量距离，矢量脱靶距离是目标和导弹在最接近处的矢量[14-17]。空空导弹仿真试验平台将脱靶距离自动输出为径向脱靶距离，作为试验结果的直观考察。

脱靶距离取决于系统跟踪精度[18-19]和系统火力控制/制导精度[20]。仿真试验中，系统跟踪精度主要由雷达导引头测量的速度测量误差和距离测量误差等表示； 制导精度由制导系统滤波处理后的估计速度误差表示。

2.1.2 定义多元回归自变量

空空导弹制导体制大多采用扩展比例导引法：

(13)

式中：N′为导航比；y为目标与导弹在垂直方向的距离，与导弹视线角有关；Tgo为导弹剩余飞行时间，与弹目距离和弹目相对速度有关；aT为目标法向加速度。由式(13)可见，测角、测速和测距的精度对制导系统的影响可见一斑。

测角信息相较于测速与测距而言更为重要，角度测量精度高可以保证目标始终在雷达天线主波束范围内，使导弹可以持续锁定，直至命中目标。导引头跟踪目标过程中，需要实时测量目标的角度信息，并给出角度信息是否可信的标志。若目标释放干扰信号或目标机动，可能会造成目标丢失，导致导引头跟踪信息的中断，从而引起跟踪不稳定。因此，导引头跟踪稳定性可以通过导引头失调角测量信息及是否可信来描述，即通过计算测角信息不可信的时间占末制导段总时间的比例，进行直接的考察。

速度的测量可以为导弹提供另一个维度的目标信息。现代雷达型空空导弹大多采用脉冲多普勒导引体制，根据武器系统提供的相对速度，检测多普勒信号，提取制导信息。导引头得到弹目相对速度测量信息后，经过处理可以得到测速信息的估计值Ⅰ，同时，根据弹目空间位置关系，导弹还可以得到另一个测速信息的估计值Ⅱ，仿真分析中，可以计算其误差，所以速度测量可以由三个参数表示，分别是速度测量误差、估计测速误差Ⅰ和估计测速误差Ⅱ。导弹与目标相对距离的测量精度同样重要，也作为考察影响脱靶距离的参数。

由于末制导段导弹飞行速度极快，导引头微小的测量误差可能导致较大的脱靶距离。为了全面考察试验数据，常将精度误差的均值、方差和中位数同时作为脱靶距离的参考量，三个统计指标相辅相成，均占有重要地位。在测量较为精确的情况下，均值、方差和中位数都应收敛于较小的数值，即统计指标与脱靶距离应呈现正相关的趋势。 如果导引头给出的测角信息持续不可信，制导系统按照滤波算法进行外推的时间将会增大，大大降低目标的追踪准确性，导致脱靶距离增大，所以导引头跟踪稳定性与脱靶距离同样呈现正相关的关系。

2.2 建立线性回归模型

构造脱靶距离的一元回归方程：

(14)

构造脱靶距离的多元回归模型：

Y=β0+β1X1+β2X2+…+β13X13

(15)

式中： 自变量与因变量的定义如表1所示；β0为回归常数；β1，…，β13为回归系数。

表1 模型变量的定义

3 回归分析与检验

通过向后选择法进行模型分析，得到脱靶距离的最优回归模型，利用标准回归系数进行自变量对脱靶距离影响程度的对比，最后检验回归模型的拟合程度。

干扰条件下的半实物仿真试验共得到了647组数据，采用的干扰样式包括： 自卫式窄带瞄准噪声和宽带阻塞噪声、自卫欺骗式多假目标和距离拖引等干扰，假目标个数取1～3个，拖引方向分为接近和远离，目标机动方式采用过载1～2的圆周机动。为了保证模型的适用性，本文仅选取后30组数据用于检验所建模型的精确程度，将前617组数据用来建立多元回归模型。

3.1 向后选择多元回归分析

通过回归建模，利用向后选择法优化多元回归模型的计算步骤如图1所示。

3.1.1 一元回归分析

建立各个自变量与脱靶距离的回归方程并且通过F检验法，统计自变量F值如表2所示。

图1 向后选择法计算步骤

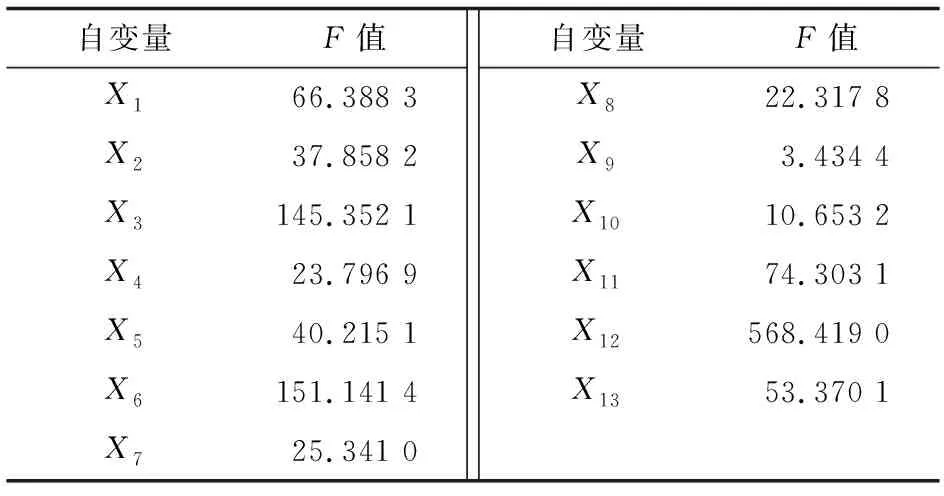
表2 自变量F值统计

由表2可见，各自变量F值与临界值对比均有F>F0.05(1,615)=1.733 8，即均与脱靶距离具有显著性关系，保留所有自变量。

3.1.2 多元回归分析

建立多元回归模型，再通过多元回归的F检验判定该方程的显著性，计算该方程的F值：

F=65.064 7>F0.05(13,603)=1.736 4

(16)

即该多元回归方程自变量与脱靶距离具有显著线性关系。

3.1.3 筛选多元回归自变量

通过t检验法，检验上述多元回归模型中每个自变量，如表3所示。

表3 自变量t值统计

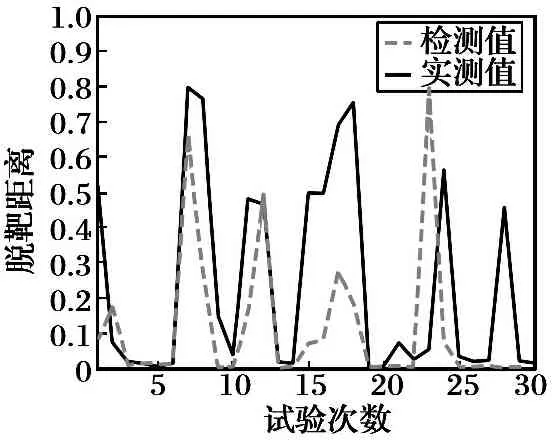
构造t统计量，并与双侧检验临界值t0.05/2(603)=1.647 4比较可得，自变量X2，X4，X7，X8，X9，X10，X11的线性关系不显著，即|t|

Y=β0+β1X1+…+β7X7+β9X9+…+β13X13

(17)

按图1所示迭代上述过程，利用保留的自变量建立新的多元回归模型，通过显著性检验，依次剔除自变量X8，X11，X2，X7，X9，X10，临界值t0.05/2(609)=1.647 4，剩余自变量t值如表4所示。

表4 筛选自变量t值统计

最终得到多元回归模型如下：

Y=-0.948 6+23.817 8X1+0.007 2X3+

0.137 6X4+0.078 2X5+0.007 9X6+

0.009 9X12+0.266 7X13

(18)

3.2 模型标准回归系数

标准回归系数[21]是指消除了因变量和自变量所取的单位影响之后的回归系数，其绝对值大小直接反应了自变量对因变量的影响程度。相对于回归系数而言，标准回归系数是一种相对的重要性，与特定情况下自变量的离散程度有关。

标准回归系数的定义为

(19)

式中：bj为Xj对应的标准回归系数；βj为原方程多元回归系数；s(Xj)为自变量Xj的标准差；s(Y)为因变量的标准差；j=1,2,…,p，p为自变量个数。

根据式(18)～(19)计算多元标准回归系数，如表5所示。

通过标准回归系数可以清晰地看到，导引头跟踪稳定性在回归模型中对因变量脱靶距离的影响远高于其他参数，与工程经验相吻合。工程中常将导引头跟踪稳定性作为脱靶距离的重要参考值； 估计测速误差Ⅰ中位数和速度测量误差中位数比其他参数影响显著，同样印证了中位数在试验数据分析中的重要地位。

表5 筛选自变量对应的标准回归系数

3.3 模型检验

将剩余30组数据代入回归模型中对其进行有效性验证。脱靶距离经归一化处理，1为有效脱靶距离远界，回归模型的拟合度检验可通过决定系数r2判断，r2是一个回归直线与样本观测值拟合优度的相对指标，反映了因变量的波动中能用自变量解释的比例[8]:

(20)

经检验，回归模型的检验有效率为69.99%，30组检验样本的脱靶距离检测值和实测值拟合情况如图2所示。由图2可以看出，检测值和实测值整体拟合程度较好，证明了所建立回归方程的有效性。

图2 脱靶距离检测值与实测值对比

拟合图中，中段拟合点8、11、15～18、23～24，以及28均出现了较大程度的失真情况，通过查考试验数据结合本文3.2节可以发现，拟合中失真点的导引头跟踪稳定性与最终的脱靶距离有较大出入，脱靶距离较大的点，导引头跟踪稳定性普遍没有相应偏大。进一步分析发现，造成此时脱靶的原因是导弹遇靶前导引头丢失目标，此刻导引头给不出有效的失调角测量信息，因此产生导引头跟踪稳定性良好但脱靶距离很大的情况。从另一方面反映出还需要引入新的变量来建立跟踪稳定性。

目前，以拖曳式诱饵为代表的角度欺骗干扰对雷达导引系统的角度测量形成巨大威胁，角度测量误差的增大会导致最终脱靶距离的增大。不同的干扰条件，对雷达型空空导弹的影响不同，本研究依据的试验数据为多种自卫式干扰条件下的试验仿真，建立的是一种综合检验模型。如果需要考察以拖曳式诱饵为代表的角度欺骗干扰下的检验模型，需要引入角度信息误差作为自变量。若考虑进一步提高检验有效性，可以将不同干扰条件下的试验分别进行建模。

本文所建立的是典型制导参数回路下的导引头测量信息检验模型，并未考虑制导系统自动驾驶仪时间常数等制导参数，若考虑这些制导系统参数对脱靶距离的影响，将有利于回归模型的优化和检测有效性的提高。

4 结 论

本文通过大量干扰条件下半实物仿真试验数据，将向后选择多元回归方法应用在雷达导引体制空空导弹参数的分析中，建立了典型制导参数回路下脱靶距离与导引头测量参数之间的数学模型，利用显著性检验筛选出具有重要影响的测量参数，并使用标准回归系数对比了影响程度，得到了约束量测参数控制侧重点的条件，最后实现了对脱靶距离的检验，研究结果表明：

(1) 导引头跟踪稳定性、估计测速误差Ⅰ方差、估计测速误差Ⅰ中位数、估计测速误差Ⅱ均值、估计测速误差Ⅱ方差、速度测量误差方差和速度测量误差中位数均与脱靶距离有显著关系，对距离误差没有显著影响，与工程经验中距离测量的重要性相对弱于角度和速度测量相一致；

(2) 通过对比标准回归系数可得，从影响程度上来看，导引头跟踪稳定性远高于其他参数，是脱靶距离最主要的衡量要素，估计测速误差Ⅰ中位数和速度测量误差中位数的影响次之，与工程应用经验相符合；

(3) 本文建立的向后选择多元回归模型对脱靶距离的检验有效率为69.99%，可以较好地检验导引头测量参数对脱靶距离的影响。