一种预测校正制导中攻角剖面的在线规划方法*
刘 刚 尤志鹏 郑宏涛
中国运载火箭技术研究院,北京100076
0 引言
近年来预测校正制导在升力式飞行器的无动力滑翔制导中获得了非常广泛的研究。文献[1-5]提出了预测校正制导的一套比较完整的方法体系。文献[6]提出了一种基于高度变化率反馈的改进倾侧角校正方法,文献[7]根据阻力加速度的反馈对攻角剖面进行0.1度的小幅调整,文献[8]用扩展卡尔曼滤波方法对综合环境参数进行在线辨识并在制导中进行补偿,文献[9]基于在线气动参数的辨识对预测过程进行在线修正,文献[10]给出一种用于火星再入的自适应预测校正制导律,文献[11]打破了事先固定攻角方案的思路,提出一种基于准三维剖面的跟踪制导方法。
预测校正制导是一种适用于升力式无动力飞行器滑翔飞行段的制导方法,这种方法通过S机动对飞行器进行能量耗散,满足制导终端的位置和速度等约束条件。在具体应用时,受到飞行器可达区的限制,当期望的终端位置不在飞行器可达区时,预测校正制导会失效。具体分为2种情况:1)飞行器能量不足。表现为当飞行器速度降低到终端速度时飞行器未达到期望的纵程或横程;2)飞行器能量过剩。表现为当飞行器到达期望终端位置时飞行器的高度或速度超出了终端约束。这2种情况一旦出现都是难以补救的。因此必须在制导策略实施前就评估飞行器可达区,当期望的终端位置在飞行器可达区内时,才能“安全地”应用预测校正制导方法;反之则应及时改变制导策略或变更期望的终端位置。基于上述考虑,本文从保证期望终端位置可达性的角度提出一种预测校正制导中攻角剖面的在线规划方法。
1 预测校正制导中可达区的快速构建
1.1 可达区的简化模型
假设飞行器正处于准平衡滑翔飞行状态,当前高度h0、速度v0,弹道倾角为0。制导终端期望高度hf,期望速度vf。可将高度和速度合并为一个反映飞行器机械能的参数e,并计算出当前能量e0和终端能量ef。
(1)
(2)
式中,g0为海平面重力加速度。在飞行器能量从e0降低到ef的飞行过程中,飞行器的可达区是一个有限的范围。文献[12-14]中分别给出了可达区计算的不同方法。典型的可达区形状如图1所示。

图1 典型的可达区形状图
可见,可达区的形状比较复杂。为了对可达区进行建模并进行可达性评估,用最大纵程Lmax、最大横程Hmax、最小纵程Lmin3个关键参数对可达区模型进行描述,如图2所示。

图2 预测校正制导的可达区
可达区简化模型由一个矩形和半个椭圆组成。可达区的轴线方向沿着飞行器在e0状态的航迹方向。椭圆的半长轴为a,椭圆的半短轴为b,焦距为c;矩形的宽度与椭圆半长轴相同,也为a,矩形的长度是f,从初始位置到矩形边的距离是d。
可达区模型的各参数用式(3)~(7)计算。
a=Hmax
(3)
(4)
b=Lmax-d
(5)
f=Lmax-Lmin-b
(6)
(7)
1.2 可达区关键参数数据库的离线计算
在飞行器能量从e0降低到ef的飞行过程中,影响最大纵程Lmax、最大横程Hmax、最小纵程Lmin3个关键参数的主要因素是攻角剖面、升力系数偏差、阻力系数偏差、大气密度偏差等。
将剖面简化为准常值攻角,即
α=α0
(8)
将升力系数偏差Δcl、阻力系数偏差Δcd和大气密度偏差Δρ三个参数重新组合为升力修正因子fL和阻力修正因子fD两个参数:
fL=(1+Dcl)(1+Dr)
(9)
fD=(1+Dcd)(1+Dr)
(10)
以α,fL和fD三个参数作为自变量,在各自的取值范围内按一定间隔进行三重循环的组合遍历,可形成多个工况。采用文献[12]中的方法对这些工况分别进行离线计算,可求得从e0到ef状态的Lmax,Hmax和Lmin的数据。
Lmax=Lmax(α0,fL,fD)
(11)
Hmax=Hmax(α0,fL,fD)
(12)
Lmin=Lmin(α0,fL,fD)
(13)
上述函数关系可分别用3维插值表的形式装订到飞行器上,作为可达区关键参数数据库。举例来说,某概念飞行器在能量为e0时,其Lmax,Hmax,Lmin与α,fL,fD的数据表(仅一部分)见表1。

表1 可达区关键参数数据
用同样的方法可以离线计算e1,e2等能量状态对应的可达区关键参数数据库,其中e1,e2在区间(ef,e0)内按一定间隔进行选取。
2 基于可达性量化评估的攻角剖面在线规划方法
2.1 可达性量化因子计算方法
构建一个可达性量化因子μ用于定量描述期望终端位置的可达性。分2种情况进行讨论,如图3所示。图中“分界线”由矩形和半椭圆的交界线延长后形成。当期望终端位置在分界线右侧时,可达性量化因子μ用于描述期望终端位置是否在半个椭圆内,根据期望终端位置与2个椭圆焦点的距离之和与椭圆的特征参数进行判断;当期望终端位置在分界线左侧时,可达性量化因子μ用于描述期望终端位置是否在矩形之内,且期望终端位置在纵向越接近“理想”纵程线、在横向越接近可达区中心线越好。

图3 可达性量化因子计算分区
以下具体给出可达性量化因子μ的计算方法。
首先根据飞行器在ef状态的期望终端位置计算e0状态的待飞纵程Lto_go和待飞横程Hto_go,并按式(14)计算待飞纵程沿当前速度方向的分量dto_go,再按式(15)和式(16)计算可达性量化因子μ。
(14)
当dto_go≥d时:
(15)
当dto_go (16) 可达性量化因子μ有如下特点: 1)当μ>1时,期望终端位置在可达区外; 2)当μ≤1时,期望终端位置在可达区内; 3)μ的值越小,期望终端位置的可达性越高。 因此可达性量化因子μ不仅可以作为期望终端位置可达性的判断依据,还可以作为攻角剖面在线规划的优化目标。 在进行攻角剖面的在线规划前需要对升力修正因子和阻力修正因子进行在线辨识。可采用一种基于扩展卡尔曼滤波的参数估计方法。飞行器再入过程中选取观测量为本体坐标系下轴向和法向的过载nx和ny。它们的表达式如下: (17) (18) 以CL,CD和ρ为待估计参数,可推导出观测矩阵为 (19) (20) (21) 其中CL0和CD0为根据飞行器上装订的气动数据插值表计算出的标称状态下的升力系数和阻力系数,ρ0为标称状态下大气密度。 攻角剖面的在线规划可以在事先选取的飞行器的不同能量状态ei,i=0,1,2,…,n-1共进行n(n≥1)次。从每次规划后到下一次规划前的时间段内,飞行器以本次规划得出的最优常值攻角作为攻角剖面。采用预测校正制导逻辑确定倾侧角指令。本文使用的预测校正制导方法中弹道积分预测方法和倾侧角指令迭代方法主要参考文献[1]。 基于可达性量化评估的攻角剖面在线规划方法,分为数据库离线构建和攻角剖面在线规划2个部分。数据库离线构建的具体流程见图4。 图4 数据库的离线计算流程 攻角剖面在线规划的思路是将在线归划问题转化为一个单变量数值优化问题,即: 攻角剖面的在线规划流程见图5。 图5 攻角剖面在线规划流程 另外,在本文的预测校正制导中除了进行攻角剖面的在线规划以外,还采取了如下措施: (a)弹道积分预测时用fL和fD对升力和阻力进行修正; (b)根据fL和fD对倾侧角反转走廊进行调整。 倾侧角反转走廊按待飞纵程进行设置,如图6所示。 图6 倾侧角反转走廊 用某概念飞行器的参数对算法进行仿真测试。飞行器采用预测校正制导时的初始状态为:高度43km、速度4100m/s,经纬度为(0,0),弹道倾角为0°,速度方向角为北偏东90°;期望的终端状态为:高度25km、速度1350m/s。对于每个蒙特卡洛仿真工况,期望终端位置在经度24±3.0°、纬度11.5±3.5°范围随机选取。制导任务示意图见图7。 图7 制导任务示意图 为了校验本文的算法,在每个工况的制导仿真中进行3次攻角剖面的在线规划,选取的能量点分别为e0,e1和e2,其中: (22) (23) 在蒙特卡洛仿真中施加最大升力系数偏差±10%、最大阻力系数偏差±15%、最大大气密度偏差±15%,并按高度施加矢量风剖面,最大风速70m/s,风向随机。 完成2000次蒙特卡洛打靶。为了对算法进行校验,对于某个工况,若最小的可达性量化因子μ*>1,仍选择“冒险飞行”,而不选择“变更期望的终端位置或改用其他制导方法”。在能量降低到ef时仿真停止,此时若纵程偏差小于15km,且横程偏差小于15km时,认为预测校正制导成功。 当μ*≤1时,若该工况预测校正制导仿真成功,则判断正确,反之判断错误; 当μ*>1时,若该工况预测校正制导仿真成功,则判断错误,反之判断正确。 2000次蒙特卡洛打靶中,预测校正制导共成功1638次(这是正常的,在一些偏差组合情况下飞行器无法达到随机给出的期望终端位置)。用可达性量化因子μ*判断期望终端位置可达性的判断正确率统计分析见表2。 表2 可达性判断正确率统计 可见,当进行多次在线规划时,其能量状态越接近终端能量状态ef,判断正确率越高,第3次规划时,判断正确率达到98.7%。 图8 第1次规划得出的μ*散布图 图9 第1次规划得出的散布图 图10 星下点轨迹包络图 为了校验本文中方法的优越性,进行2组对比仿真。 第1组:不进行攻角剖面在线规划,采用接近最优升阻比的8°固定攻角; 第2组:在e0能量点进行1次攻角剖面在线规划; 将3.1节的仿真作为第3组。以上三组仿真除了攻角剖面的策略不同,其余所有策略和参数都相同。将第1组和第2组分别完成2000次蒙特卡洛仿真,将三组仿真结果进行对比,总成功率见表3。 表3 三组仿真的总成功率对比 由表3可见,相比于采用固定8°的攻角剖面,使用本文的方法,进行1次攻角剖面在线规划后预测校正制导的总成功率提高了3.8%;进行3次攻角剖面在线规划后,预测校正制导的总成功率提高了5.55%。 以典型的第479号工况为例,采用8°固定攻角时预测校正制导失败,采用3次攻角剖面的在线规划后预测校正制导成功,该工况的仿真曲线如图11~16所示。 图11 第479号工况高度曲线 图12 第479号工况速度曲线 图13 第479号工况指令攻角曲线 图14 第479号工况指令倾侧角曲线 图15 第479号工况风攻角曲线 图16 第479号工况地面轨迹 提出一种预测校正制导中基于可达性量化评估的攻角剖面在线规划方法。基于可达区的3个关键参数和期望的制导终端位置,构建了一个可达性量化因子。该因子可以用于对飞行器能否到达期望的终端位置进行在线判断,也可以作为攻角剖面在线规划中单变量数值优化问题的目标函数。蒙特卡洛仿真表明,对于多次规划,可达性判断的正确率逐步提高,第3次规划时判断正确率达到98.7%;另外,相比于采用接近最优升阻比的固定的攻角剖面,进行1次攻角剖面在线规划后预测校正制导的成功率提高了3.8%,进行3次攻角剖面在线规划后预测校正制导的成功率提高了5.55%。本文的方法尤其对于升力式飞行器的制导策略在线决策和优化具有参考和应用价值。2.2 升力修正因子和阻力修正因子的在线辨识

2.3 基于可达性量化评估的攻角剖面在线规划的思路和流程
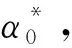




3 蒙特卡洛仿真校验
3.1 相关参数
3.2 可达区判断正确率校验


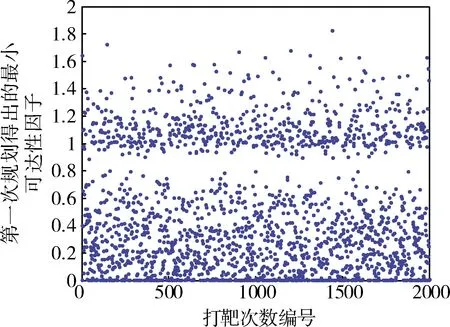
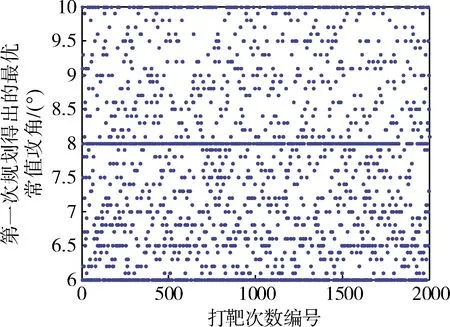

3.3 预测校正制导总成功率对比

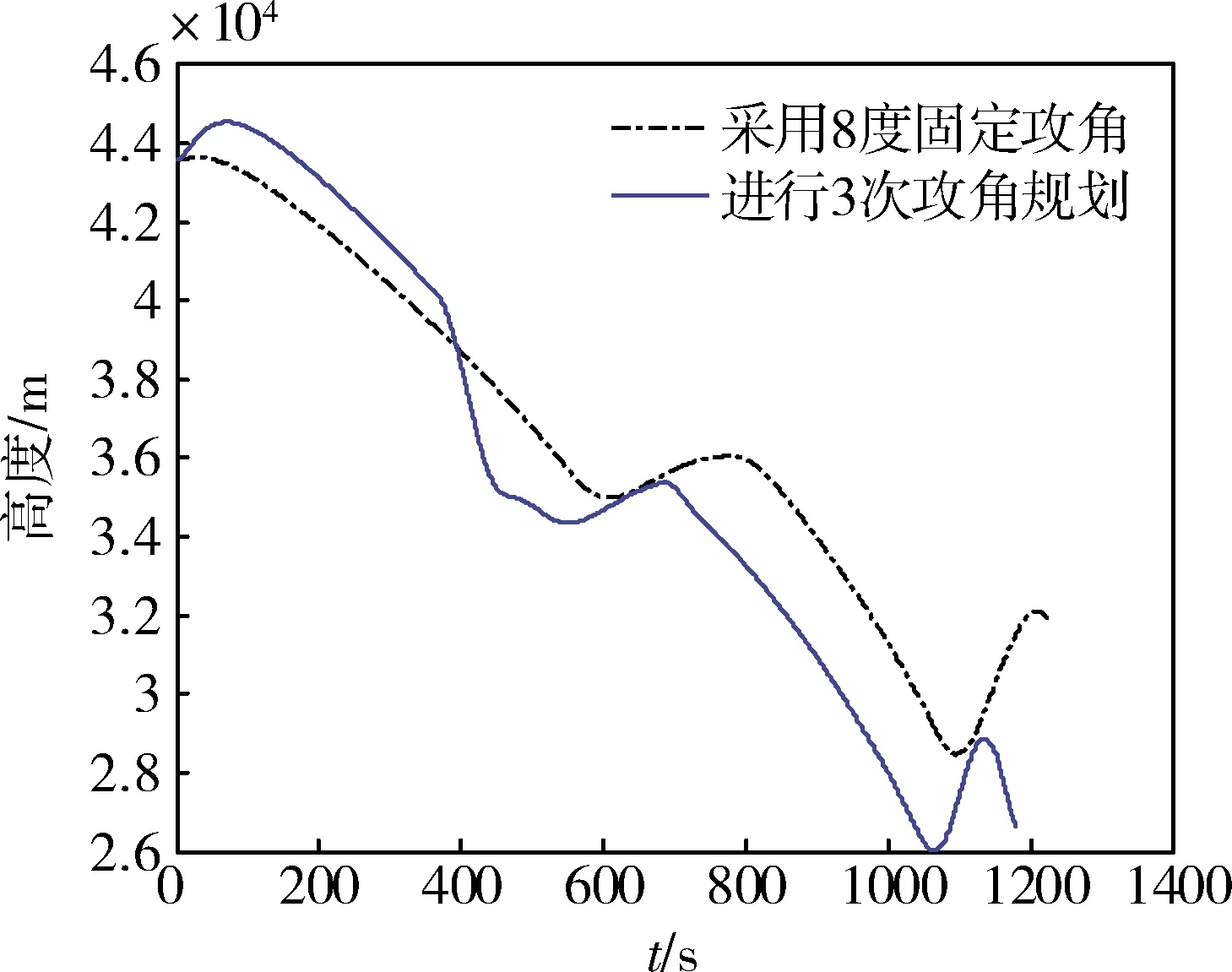





4 结论

