白光干涉垂直扫描测量算法综述

汝洪武,张文喜,吴玲玲

(1.西安工业大学光电工程学院,陕西 西安 710021;2.中国科学院空天信息创新研究院计算光学室重点实验室,北京 100094)

1 引 言

白光干涉测量解决了单色激光干涉测量的量程较小,精度不足的问题,在干涉定位和非接触式测量方面有广泛的应用[1]。白光干涉多采用垂直扫描法进行测量,如图1所示。光源出射光准直后被分光镜(BS)分束,分别到达测试面和标准面后得到表面信息,反射光束再被BS合束后到探测器,采用压电陶瓷(PZT)线性位移机构调整参考光路的光程差进行扫描测量。白光干涉测量不同于单色光源干涉测量,白光光源一般功率大、光谱较宽[2]。两路相同波段的激光重合时会产生干涉现象,把这两路激光称为“激光对”,单色光干涉产生的条纹对比度是稳定的[3-5]。白光干涉是无数不同波段的“激光对”的干涉的相互叠加,且不同波段的干涉条纹宽度不同,随着光程差的增大干涉光强被均匀化,光强对比度为零,只有在参考光与测试光光程差为零时无数条激光干涉的波峰在同一处重合,此处光强最强。

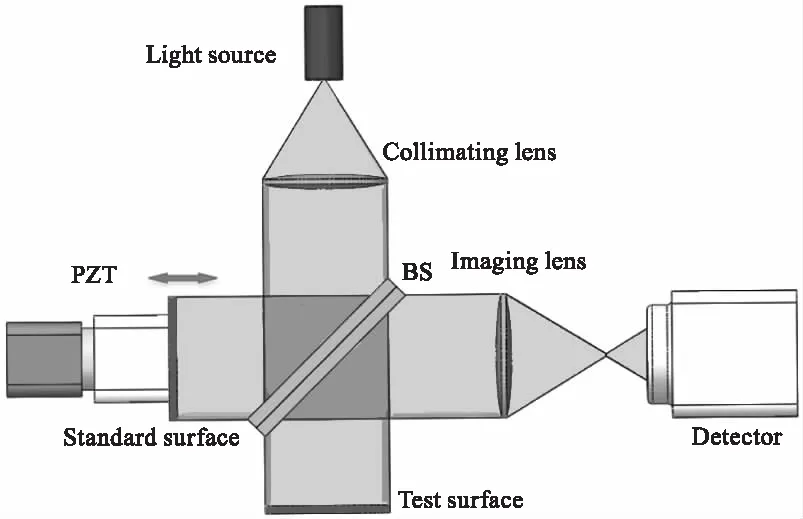
图1 迈克尔逊白光干涉系统

稳定双光束干涉的光强信号可以表示为[6]:

(1)

相干峰寻址法根据白光信号相干长度短、相干峰明显的特性提出的:以高度不同的两点为例,扫描测量的过程中两点依次出现相干峰,以相干峰峰值点的位置为参照,两个相干峰峰值点在Z轴上的差值就是两点的高度差,如图3所示。实现相干峰寻址法的具体算法很多,不同的算法具有不同的相干峰定位精度和不同的特性,选择合适的算法尤为重要。

图2 模拟白光干涉信号

图3 相干峰寻址法

2 白光扫描干涉信号算法

将相干峰寻址法分为三大类:直接求解法、包络曲线拟合法和加权平均法。不同算法的特性直接决定了白光干涉信号的相干峰定位精度。在同等算法的条件下,采样点越密集精度越高。

2.1 直接求解法

2.1.1 插值法

插值法在相干峰峰值点处选取三个干涉数据,代入一元二次方程后求得极值点横坐标代替对应的峰值点位置[7]。表面高度信息h的计算表达为:

(2)

其中,i为光强最大值处的横坐标值；Ii为对应位置i处光强值。插值法每组数据只用了峰值附近的三个数据点,计算速度快、精度低,适用于精度不高的应用场合,提高插值法的测量精度可以通过多次测量求均值、提高步进精度、减小白噪声误差或减小扫描间隔。

2.1.2 移相法

移相算法根据白光干涉光强公式的基础上得出,在峰值附近选取几个采样点,解方程计算出峰值点的相位φ,如式(3)所示,再通过光源参数计算求得表面高度。移相法又有三步移相法、四步移相法、五步移相法等多步移相法[8-9]。以四步相移法为例,计算公式如式(4)所示。

(3)

(4)

移相法利用峰值附近的几个数据,计算速度快,充分利用了光强和相位两种信息,计算精度高。因为数据点较少,分母上差值准确性降低,分母较小时受到白噪声影响较大。移相计算方式可以在一定程度上不受扫描间隔大小的影响,降低对高精度移动平台的依赖。

2.1.3 空间频域法

空间频域法Peter de Groot等人提出[10],是现阶段计算精度相对较高的方法[11-12]。只通过白光干涉信号的相位信息计算待测面形。单色光发生干涉时相位与波数和光程差成正比,白光干涉信号是很多单波长光产生干涉信号的叠加,将其相位在空间角频率k0处用泰勒级数展开,得到:

(5)

其中,第一项Φ0=k0Z0,为k=k0处的相位分量;Z0为k0的相速度光程差。通过相位解包裹的方法消除周期性2π的相位模糊,保证相位计算的连续性。将常数项k0Z0来进行优化,该常数项通过直线拟合后的直线函数信息获得。优化后如下[13]:

(6)

其中,n为传播介质的反射率系数；α为相位补偿量；n,α由材料所决定。

空间频域法摆脱白光干涉测量对干涉光强对比度的依赖,仅在频域内进行处理,以相位与空间角频率之间关系的斜率求得待测面形信息,计算精度高,相比傅里叶变换和高斯拟合具有更小的运算量,信号处理迅速。在信号处理时,即使测量时存在一定的2π周期的相位模糊也并不影响斜率的计算,因此采样过程中采样间隔π/2与5π/2,计算结果一致,可用于欠采样时的情况下。

2.2 加权平均法

2.2.1 重心法

重心法是基于加权平均提出的,把光强值看作为权值,对应的横坐标看作待求平均的数据,得到的加权平均的值就是相干峰的坐标值[14-16]。即相干峰峰值的横坐标信息可以表示为:

(7)

但是上式的计算精度受白光干涉信号的背景光强值影响较大。Veeco的Ai等人对重心法进行了改进,有效降低了背景光强的影响[17],如下式:

(8)

其中,令mi=(Ii-Ii-1)2代替原始信号的光强值作为权值,重心算法的速度和效率都很高,但受背景光强的影响很大,适用于背景光强相对较小的测量环境。改进后的重心法能有效的降低背景光强的影响,使用重心法求解的过程中尽可能峰值所处的位置在于数据的中心位置,可以有效的提高重心法的计算精度。

2.2.2 相干相关算法

相干相关算法(Coherence Corelation Interferometry,CCI)由泰勒霍普森公司提出[18-19]。首先根据采用的光源的参数模拟出参考白光干涉光强信号ai,将模拟信号与实际采集到的扫描信号点对点相乘,然后将参考信号沿X轴方向逐步平移,记录下每步参考信号ai与白光干涉光强Ii的乘积,用该数据代替白光干涉信号[20]。具体如下式:

(9)

Ai呈高斯分布,对其高斯拟合后找到高斯拟合曲线的最大值的横坐标即待测表面高度。

相干相关算法与小波变换包络拟合法极为相似,但是没有小波变换的灵活度高。适用于欠采样的情况,能保持相对可观的计算精度。由于每组数据都需要多次计算,并且再进行拟合取极值横坐标值,计算量很大,相对较为耗时。

2.3 包络曲线拟合法

包络曲线拟合法根据白光干涉包络曲线的形状拟合的函数曲线,或利用经过各种变换处理后的包络曲线进行拟合,用该曲线的峰值点来代替实际相干峰的峰值点,很大程度上提高了白光干涉的相干峰定位精度,主要包括以下几种算法。

2.3.1 多项式拟合

多项式拟合法由Park和Kim提出[20],根据白光干涉光强的包络曲线符合高斯分布,在峰值附近的包络曲线接近于一个一元二次方程的函数曲线在峰值附近的包络形状,因此用二次多项式对白光干涉光强的包络曲线进行拟合。具体过程如下所示:

I(z)=Ibg-Ibg(a1+a2z+a3z2)(cosθcosρ+sinθsinρ)

(10)

(11)

多项式拟合宜取相干长度范围内的数据用以拟合,便于保证实际数据与二次曲线的重合程度更高,提高拟合结果的逻辑缜密性。多项式拟合法优势在于对数据利用更充分,具有相对较强的白噪声抑制能力。但是数据量更丰富的同时计算量增大、计算时间变长。

2.3.2 高斯拟合法

白光干涉光强曲线符合高斯包络调制,对白光干涉光强的高斯包络进行拟合,取其极值点的横坐标就是该点对应的相干峰的坐标h[21]。其计算公式如下:

(12)

高斯拟合算法相对简单,当扫描间隔稳定时计算精度也相对较高,还适用于欠采样的测量过程,当扫描间隔较大时可以采取对数据先减其均值后再取绝对值,数据密度增加了一倍,高斯拟合法对扫描间隔的依赖性较低。高斯拟合法对扫描间隔的大小要求相对较低,但是当扫描间隔过大时精度也随之降低,且高斯拟合法计算量大,计算时间较长。

2.3.3 傅里叶变换

傅里叶变换法是适用性比较广泛的一种算法,将采集到的白光干涉信号傅立叶变换,滤去正弦调制项的频率,逆变换后得到白光干涉数据的高斯包络曲线的相干峰峰值点坐标。傅里叶变换法本质上是滤除自身载波的影响,因此也被称作傅里叶滤波法,分析如下式[22-23]：

(13)

其中,*表示对函数的卷积。白光干涉信号的包络曲线与傅里叶逆变换后得到的幅值曲线成正比,即白光信号的峰值点与该曲线的峰值点重合,对上式的幅值曲线高斯拟合即得表面高度。

傅里叶变换算法的计算精度高,对白噪声抑制能力强,不足之处需进行正反两次变换和高斯拟合,计算量大,计算时间长,且傅里叶变换只反映整体信息,对局部窗口的信息反应不够全面。傅里叶变换法要求扫描间隔不能过大,否则可能会导致采样频率提取无效,只适用于采样间隔相对不大的测量环境。

2.3.4 希尔伯特变换

希尔伯特变换法将原始信号加上经过希尔伯特变换的虚部信号构成的复信号,得到的信号的频率全是正频部分[24]。提取信号包络的过程通过希尔伯特变换完成,即希尔伯特变换可得白光干涉测量的峰值点。设Iac为白光干涉信号的交流部分,变换后Iac产生了-90°的相移。在调制信号逐渐变化、载波信号迅速变化的情况下,交流信号的希尔伯特变换近似表示为[7]:

(14)

希尔伯特变换与傅里叶变换的计算精度相近,要求采集信号中的背景光强足够稳定。实际测量时,参考面的移动过程当中距离光源的位置发生改变,背景光强随之改变。但希尔伯特变换法是一种时域内的变换,不需要从频域向时域的逆变换和高斯拟合过程,相比傅里叶变换法就有更快的计算速度,更容易引入测量误差。

2.3.5 小波变换法

小波方法是在傅里叶变换的基础上优化出的。傅里叶变换仅采用正弦波作为变换的基础波形,而小波变换采用特殊的曲线线段或者向量作为变换的基础波形,可以用自己定义的一个波形作为变换的基,扩大了频域信号分析方法中的时频适用性[25-26]。小波变换有两个可变的参量,所以小波变换具有对目标信号进行有选择性的分段分析,实现不同波段进行不同频率滤波的功能。设Ψ(t)为一个小波族的基波,则将小波族定义为:

(15)

式中,a,b为常数。通过调整参数a、b来调整上式的幅值大小和坐标位置。小波变换定义为:

(16)

其中,X(t)为任意平方可积函数。针对小波变换双参数可调的特性,提出了两个白光干涉信号的峰值点的寻址方法:小波包络峰值点提取以及连续小波变换法。

(1)小波包络提取

根据不同使用情况下选择适合的基,小波包络提取时直接选择白光干涉信号的波形作为母小波。由法国地震学家J.Morle提出的Morlet小波[25],它是一个受复数信号调制的高斯包络信号,通过提取包络信号的极值点对应的横坐标,得到变换的目标结果[25]。由下式所示:

(17)

定义|WT(a,b)|为小波系数,其中WTmr(a,b)和WTmi(a,b)分别为小波系数的实数部分和虚数部分,调整b的大小实现子小波与实际信号会发生小距离的错位,当小波系数最大时,小波函数的峰值点与白光光强包络的峰值点重合,子小波峰值点的位置代替干涉峰峰值点所在的位置。模拟的小波包络如下式:

(18)

(2)连续小波变换

连续小波变换充分利用小波变换的两个可变尺度参数a调整光源的中心波长,b调整相干峰位置。当小波函数与干涉光强曲线I(z)在频域与时域都重合时,小波系数最大[26]。此时的相干峰信息确定方式如下式[26]:

(19)

其中,h′为对应着小波系数最大时小波函数峰值点对应的坐标,相位信息通过下式可得:

(20)

其中,[WT(a,b)]是小波系数的最大值,表示b0处Morlet小波与I(z)之间的相位差。

小波变换法相对于傅里叶变换法具有较强噪声平滑作用,对噪声具有很强的抑制效果的同时不损伤数据的边缘信息,能够获得每个频段的完整信息[27-28]。小波变换在时域和频域中同时具有非常好的调控能力,可以针对目标信号的任意波段进行分析,有利于更全面的对所获得的数据获取更多的信息,在科学研究中应用非常广泛。但是小波变换算法的计算量相对较大,计算速度较慢。

2.3.6 基于采样定理的平方包络函数估计算法(SEST)

基于采样定理的平方包络函数测量(SEST)方法的提出是为了解决白光干涉测量时数据量庞大的问题,有效地降低了白光干涉测量对高密度采样的依赖性,在欠采样测量过程中应用比较广泛[29]。用采样数据信号点Ym(m=l,2,…,M)定义一个新的向量如式(21),作为原始干涉信号进行处理。

(21)

式中,f(z)是干涉光强分布中的干涉项,可以定义为ym=f(zm),zm是第m个采样点。则φm(z)定义为:

(22)

(23)

式中,Δ是采样间隔。找到包络曲线的峰值点就能解算出待测面的面形信息,不需要严格的复现干涉图的信息,式(24)是一个基于采样数据对r(z)的估算值rB(z),其包络曲线最大值对应的横坐标就是对应坐标点的表面高度h。当z是其中的一个采样点,定义:z=zj(j=1,2,3,…M)。

(24)

SEST算法是针对扫描间隔较大的情况提出的,适用于欠采样的测量过程中,虽然小幅度增加了计算时间,但是大幅度减少了采样时间,另外可以适用于生产线上的快速测量,降低了垂直扫描干涉法对高精度移动平台的高度依赖,并且具有较高的计算精度。

3 计算结果

表1是在一组仿真的白光干涉信号,仿真光强的中心波长为633 nm,相干长度为50 μm,扫描长度为80 μm,单组数据有120个光强值,从计算精度、扫描步长、运算速度和白噪声影响四个方面对各种算法做了仿真分析,得到以下结果。

表1 各种算法的性能对比

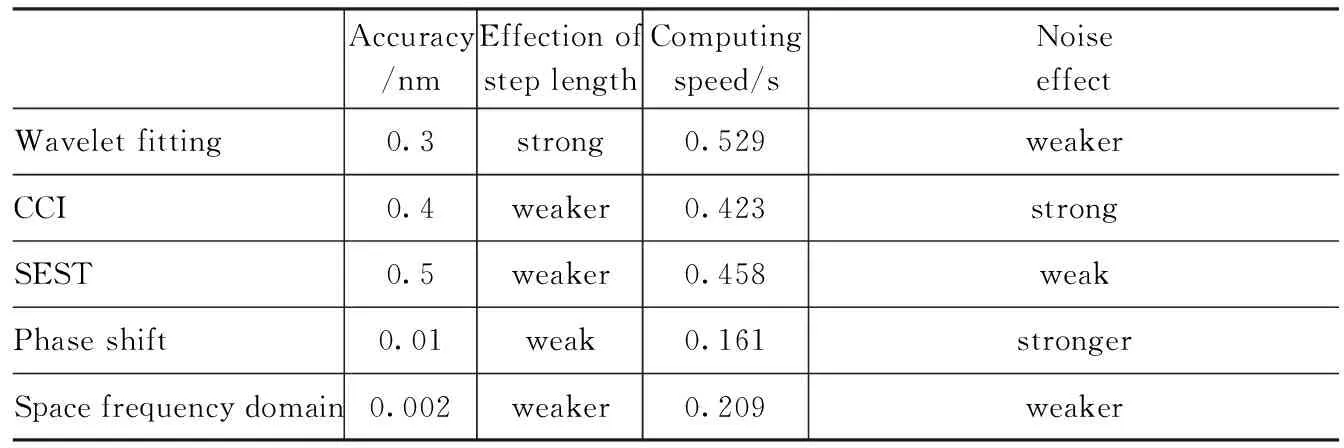
(续表)

4 结 论

白光干涉测量具有算法精度高、量程大等优点,广泛应用于各种高精度、大量程的干涉测量当中。白光干涉测量算法种类较多,需要根据实际测量的条件和环境灵活选择适合的算法,也可采用多种算法组合使用。了解各种白光干涉测量算法的特性、选择适当的算法对提高白光测量的精度具有非常重要的意义。

根据仿真结果得出几点结论:①相干相关算法、空间频域法、移相法、小波变换法和采样定理的平方包络函数估计算法在未知光源参数的情况下不能使用,可优先采用其他几种算法;②相移法和插值法只需要峰值附近的几个数据就可实现测量,计算精度快,可在在线测量或者快速测量的情况下优先采用。其中相移法测量精度相对较高;③重心法、相干相关算法、空间频域法和SEST法受扫描步长的影响较小,可用于欠采样情况下;④傅里叶变换法、小波变换法和空间频域法具有较强的噪声滤除能力,可用于探测器噪声相对较大的情况。