基于激光回馈效应的应力测量系统研究
孟媛媛,牛海莎,董明利,陈 恺,庄 炜
(1.北京信息科技大学仪器科学与光电工程学院,北京 100192;2.合肥工业大学仪器科学与光电工程学院,安徽 合肥 230009)
1 引 言
玻璃材料的内应力直接影响玻璃零件加工质量和光学器件使用寿命,在航空航天、精密光学系统、精密加工等领域受到高度重视。高灵敏度,大测量范围的应力检测技术已经成为当前的研究热点。材料内应力的测量方法可分为两大类,即机械测量方法和物理测量方法。机械测量方法起源于19世纪末期提出的 “钻孔法”,即在应力平面钻孔,通过应力释放过程中孔发生的形变获得应力大小。后来学者们对这些机械测量方法进行了改进[1],但破坏性测量限制了该方法在许多领域的应用。物理测量方法属于无损测量,典型的测量方法有X射线衍射法[2-3]、超声法[4-5]、简式偏光仪[6]、 Senarmont补偿法[7-8]等。X射线衍射仪价格昂贵,多用于测定物质的晶体结构进行物相分析;简式偏光仪结构简单,但只能通过干涉色定性观察应力分布且无法察觉微小应力。
超声法测量应力原理简单,设备轻便,可以实现现场或在役检测。但是鉴于材料本身的密度变换、尺寸测量精度等因素的干扰很大,同时由于高分子材料的广泛应用时间不长、其物理性质与金属有明显区别等因素,有关航空玻璃超声检测的研究、尤其是表面波的应用研究至今仍未取得令人鼓舞的成果。文献[9]与文献[10]曾利用超声法对透明件表面应力进行了测量,但均未获得理想结果。综合以上原因,超声法测定残余应力尚未在高端玻璃应力实测方面得以推广应用。
激光回馈具有类似传统双光束干涉的特点,又具有结构简单、自准直、灵敏度高、不受相干长度限制等多种优点,因而获得了研究人员的关注。在激光回馈测量技术中,激光器不仅仅是光源,同时还兼具传感器的作用,已在速度[11]、位移[12]、绝对距离、振动[13]、形貌[14]和相位延迟[15-17]等多种测量领域获得了研究和应用。本文提出一种基于激光回馈效应的应力测量方法,激光回馈系统由激光器和外部反射镜构成,待测样品放置在回馈外腔中。由于应力引起的双折射效应,带有应力的样品使外腔分裂为两个“物理长度”,不同的外腔长决定了不同偏振方向的回馈光相位,通过提取相位差信息,可获得应力的大小。从理论上分析了回馈系统中激光器的输出光在正交方向的相位与外腔应力双折射的关系;通过傅里叶变换的方式得到双折射外腔激光回馈系统光强调谐曲线的相位信息;最后,采用激光回馈系统对不同的飞机座舱有机玻璃样品内应力进行了测量,并给出测量结果。该方法具有结构简单、精度高的优势,并且具有应用于玻璃材料生产线、改进制备工艺的潜力。
2 实验设置及原理
实验设置如图1所示,激光器为线偏振、单纵模输出的He-Ne激光器,波长为632.8 nm,激光增益管长为145 mm。M1和M2构成激光器的谐振腔,腔长为155 mm。M1为凹面输出镜,反射率为99.5 %,M2为平面高反镜,反射率为98.9 %。ME为回馈镜,反射率约为4 %。增益管内充氦气和氖气的混合气体,混合比例He∶Ne=7∶1,且Ne20∶Ne22=1∶1,以消除兰姆凹陷。D1和D2为光电探测器,输出端的光被沃拉斯顿棱镜W分开,分别由D1、D2探测。回馈镜与PZT2粘连,PZT2在施加三角波电压后推动回馈镜做往复运动。

图1 实验设置
以激光器的传播方向为Z轴建立坐标系,激光器的本征偏振态分别为E1和E2,起振的偏振态为E1,E1与X轴、Y轴的夹角为45°,沃拉斯顿棱镜的光轴方向分别平行于X轴、Y轴。首先旋转沃拉斯顿棱镜使出射光点只有一个,此时沃拉斯顿的两个光轴方向之一与激光器的初始偏振态平行。再将沃拉斯顿棱镜旋转45°,即可使激光器的光强沿着正交方向均匀分光。当外腔未放置波片时,激光沿X、Y方向分光以后,得到的光强分量等幅度、等相位。
旋转波片使波片快轴方向与激光器初始偏振方向平行,此时激光器的输出偏振态仍为单模、线偏振,在X、Y方向的输出光强仍为等幅、等相位的类余弦曲线。再次将波片以激光传播方向为轴心旋转45°,假设波片的相位延迟大小为σ,以激光器的初始偏振态为X′ 轴,则激光器的输出光仍表示为E1,线偏振光穿过外腔中的波片、并被反射镜反射再次通过波片,进入内腔时的偏振态可表达为:
(1)
由式(1)可知,回馈光的偏振态为椭圆偏振态,且X′ 方向的振幅为cosσ,Y′ 方向的振幅为sinσ。随着外腔中波片相位延迟的变化,回馈光偏振态与激光器本征偏振态可以由图2表示。

图2 回馈光偏振态与激光器本征偏振态
当外腔中存在椭圆偏振态的回馈光时,激光器的输出在正交方向不再等幅、等相位。为解释该现象,光场被分为两个部分,一部分在激光内腔中往返一周,另一部分被外腔镜反射,在外腔中往返一周后再次回到内腔,如图3所示。根据激光器的自洽条件,这两部分光场叠加后应满足激光器输出稳态方程。

图3 三镜腔模型
对各物理量的定义如下:L为激光器谐振腔的几何长度,l为回馈腔的几何长度。设某时刻输出镜M2内侧的光场为E0,当回馈光在外腔中往返一周后回到内腔,引入的光场为:
(2)
其中,k为波数;n0,n分别为激光器内与回馈外腔的介质折射率;λ为激光器的波长;t2为M2的透射系数;re为回馈镜ME的反射系数;ξ为回馈光的耦合效率[10];g为增益介质在单位长度的增益系数。内腔光场在谐振腔中往返一周后可表示为:
(3)
其中,r1和r2分别为M1和M2的反射系数,两部分光场的叠加应与初始光场相同,则有:
(4)
其中,ρ=T2r3ξ/r2;T2=t22为M2的透过率;φ为外腔相位因子且φ=2knl。因为T2r3ξ远小于r2,因此ρ远小于1。根据激光自洽条件,有:
|r1r2e2ikn0L+2gL|=r1r2e2gL|e2ikn0L|=1
(5)
解得:
(6)
且有:
|e2ikn0L|=1
(7)
无光回馈时激光的增益系数为g0,将式(7)代入式(6)可得:
|r1r2e2gL(1+ρeiφ)|=1
(8)
展开指数项可得:
(9)
由于ρ远小于1,上式可化简得:
r1r2e2gL(1+ρcosφ)=1
(10)
两边取对数并化简可得:
(11)
比较有回馈和无回馈时的增益变化量可知,回馈引入的增益波动为:
(12)
激光的输出强度与增益系数成正比,可得激光回馈条件下的输出光强为:
I=κg=I0(1+κΔg)
(13)
外腔中放入波片后,因为波片的两个光轴方向存在相位延迟量σ,两个光轴方向的光程差为:
Δ=(2πm+δ)λ,m=0,1,2,…
(14)
因此两个光轴方向存在的光程差,由此产生的则相位因子差异为:
(15)
从以上推导可得,光强调谐曲线在X轴、Y轴方向的分量存在相位差,且相位差与波片相位延迟σ有函数关系,理想情况下,相位差为波片相位延迟的两倍。
3 实验结果及分析
随着外腔相位延迟大小的改变,激光器的输出在正交方向的分量呈现出不同的幅值和相位特性,实验结果如图4所示。
通过傅里叶变换的方式得到双折射外腔激光回馈系统光强调谐曲线的相位信息,分别用0°~180°范围内的2组不同厂家加工的波片进行了双折射外腔回馈实验,其中横轴的结果由线偏振光回馈法得出,纵轴结果由相位差法得出,结果如图5所示。


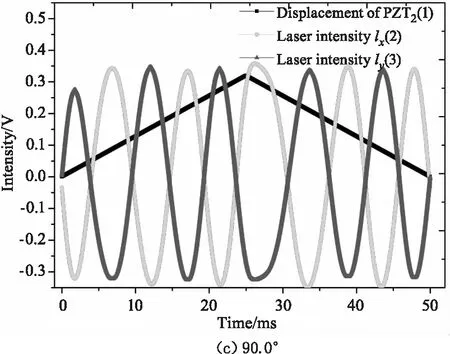

图4 实验结果
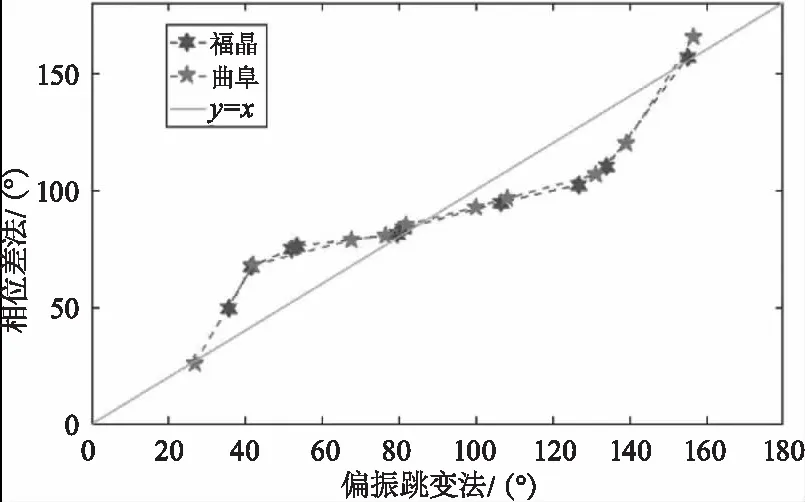
图5 相位差法与跳变法的比对
线偏振光回馈的偏振跳变法精度优于0.3°,相位差法与之比对两套波片的走势一致,但相位差法具有一定的误差。这是由于增益管本身带有一定的各向异性,且回馈光的偏振态为椭圆偏振态,导致回到谐振腔内的光被放大的方向并非沿本征偏振方向,因此正交分量的相位差与2倍关系有偏差,且幅值比也随回馈光椭偏度的改变而改变。由于相位差法提取外腔应力双折射信息是通过两束同步变换的类余弦信号,外界干扰对两路测量信号的影响是同步的,该影响在求相位差的时候可抵消,因此,相位差法较偏振跳变法具有更好的重复性。将相位差法的测量结果校准到偏振跳变系统,可得拟合如下:
f(x)=-2.507e-11x7+1.548e-8x6-3.861e-6x5+0.0004976x4-0.03496x3+1.275x2-19.08x+84.52
拟合函数曲线如图6所示。经校准后,相位差法的精度优于0.5°(转换为632.8 nm下的光程差值为0.88 nm),重复性优于0.1°。实验系统采用的激光器波长为632.8 nm,根据:
可得系统对应力引起光程差的测量精度为0.879 nm。
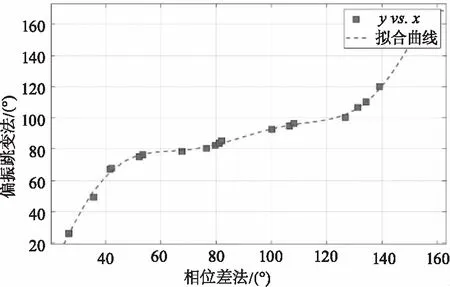
图6 拟合函数
采用激光回馈双折射测量系统对2块有机玻璃样品(清华大学航天航空学院提供)分别进行测量,2块样品均为20 mm×20 mm的矩形,厚度分别为4.615 mm,8.580 mm。每块样品测试4个角(A-D点)和中间点(E点),环境温度为20.2 ℃,测量得到样品内部的内应力如表1所示。

表1 应力测量结果/nm
4 结 论
本文提出一种基于激光回馈效应的应力测量方法。从理论上分析了回馈系统中激光器的输出光在正交方向的相位与外腔应力双折射的关系;通过傅里叶变换的方式得到双折射外腔激光回馈系统光强调谐曲线的相位信息;最后,采用激光回馈系统对不同的飞机座舱有机玻璃样品内应力进行了测量,并给出测量结果。该方法重复性优于0.1°,精度优于0.5°,具有结构简单、精度高的优势。

