基于正交试验大跨PC连续刚构桥主梁参数优化研究

蒋玮，周群，李莘哲

(1.广西路桥工程集团有限公司，广西 南宁 530000；2.广西路桥集团勘察设计有限公司)

大跨PC连续刚构桥主梁参数众多，受力复杂，设计者往往凭借以往经验和参考已有设计或类比试算来选取参数。然而，实际工程中因主梁参数选取不合理而导致主梁受力不佳出现多种病害的实例不在少数，更有甚者直接导致安全事故的发生。因此，对主梁参数进行优化研究，为主梁参数合理选取提供行之有效的科学指导显得十分必要。

文献[5-7]采用遗传算法、遗传算法与神经网络结合、响应面法等方法对主梁参数优化进行研究，虽能够得到在经验范围之内的精度较好的优化结果，但这些方法理论过于深奥，需要大量样本数据反复计算，不便于被工程人员掌握，实用性较差，难以推广应用；文献[8-10]均以某一座大跨连续刚构桥为研究对象，利用正交试验设计思想，通过改变主梁设计参数，以主梁跨中应力、挠度、混凝土数量为优化指标建立综合目标函数，通过对计算结果的分析，得出主梁跨中性能最优参数组合，但研究仅选取主梁跨中截面下缘应力作为优化指标，存在缺乏对主梁全截面应力考核的不足，且均选取一种跨径进行研究，其结论是否适用其他跨径难以确定。

为进一步深入研究大跨PC连续刚构桥主梁参数的合理取值，该文基于正交试验法，选取主梁边主跨比、梁底曲线幂次、跨中高跨比、支点高跨比作为主梁优化参数，建立以主跨全截面平均应力、跨中最大挠度、混凝土数量为优化指标的综合目标函数，间隔10 m建立主跨100～150 m之间6种不同跨径的有限元参数试验模型，通过对有限元结果的计算与分析，研究主梁参数的最优组合，为主梁参数选取提供更科学可靠的理论指导。

1 工程背景简介及有限元模型建立

1.1 工程背景简介

背景工程为某山区高速公路一座三跨PC连续刚构桥，桥跨布置为(72+120+72)m，上构主梁为单箱单室箱梁，C55混凝土，桥面总宽12 m，顶板厚0.28 m，变截面梁高由跨中3.1 m渐变至支点7.0 m，按二次抛物线进行渐变，其横断面如图1所示。底板厚由跨中0.32 m渐变至支点0.7 m，渐变规律同梁高，底板总宽6.5 m。

图1 主梁支点与跨中横断面图(单位：cm)

下构为双薄壁墩，横向壁宽6.5 m，顺向壁厚1.5 m，双肢中心间距7.0 m，墩高40 m，C40混凝土。

1.2 有限元模型建立

采用最新Midas 2019按实际施工过程建立结构整体有限元模型(图2)，上构为C55混凝土，下构为C40混凝土，全桥共划分为184个梁单元，其中上构104个梁单元，下构80个梁单元。

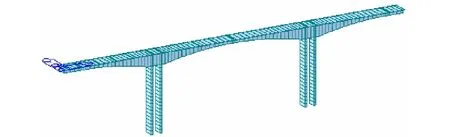
图2 整体有限元模型图

2 主梁优化参数选取与正交试验设计

2.1 主梁优化参数选取

根据文献[1-4]及笔者对中国已建及在建大跨近100座PC连续刚构桥主梁参数统计可得，主梁边主跨比多数为0.52～0.6，梁底幂次为1.6～2.0，跨中高跨比为0.02～0.03，支点高跨比为0.052～0.067。因此，该文主梁4个优化参数选取范围即在以上统计范围之内，每个优化参数选取4个参数值进行试验，其试验参数水平表如表1所示。

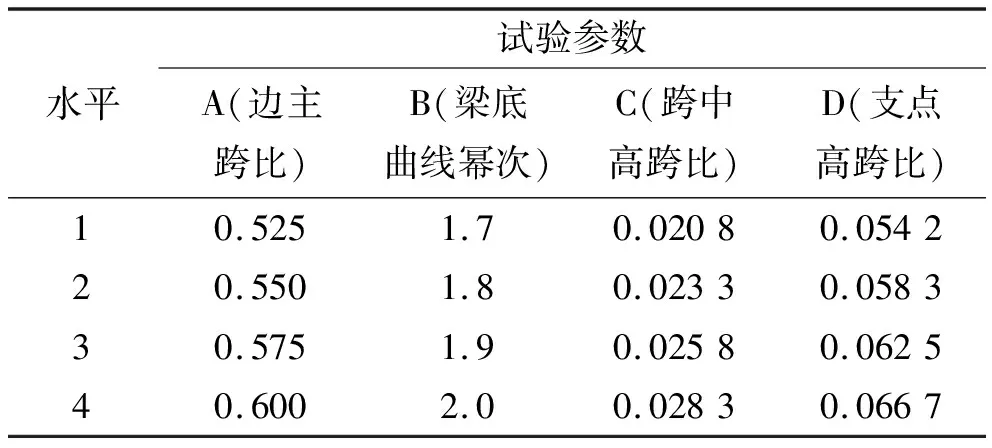
表1 主梁试验参数水平表

2.2 正交试验设计

该文选用的正交表L16(44)及试验参数正交表如表2、3所示。

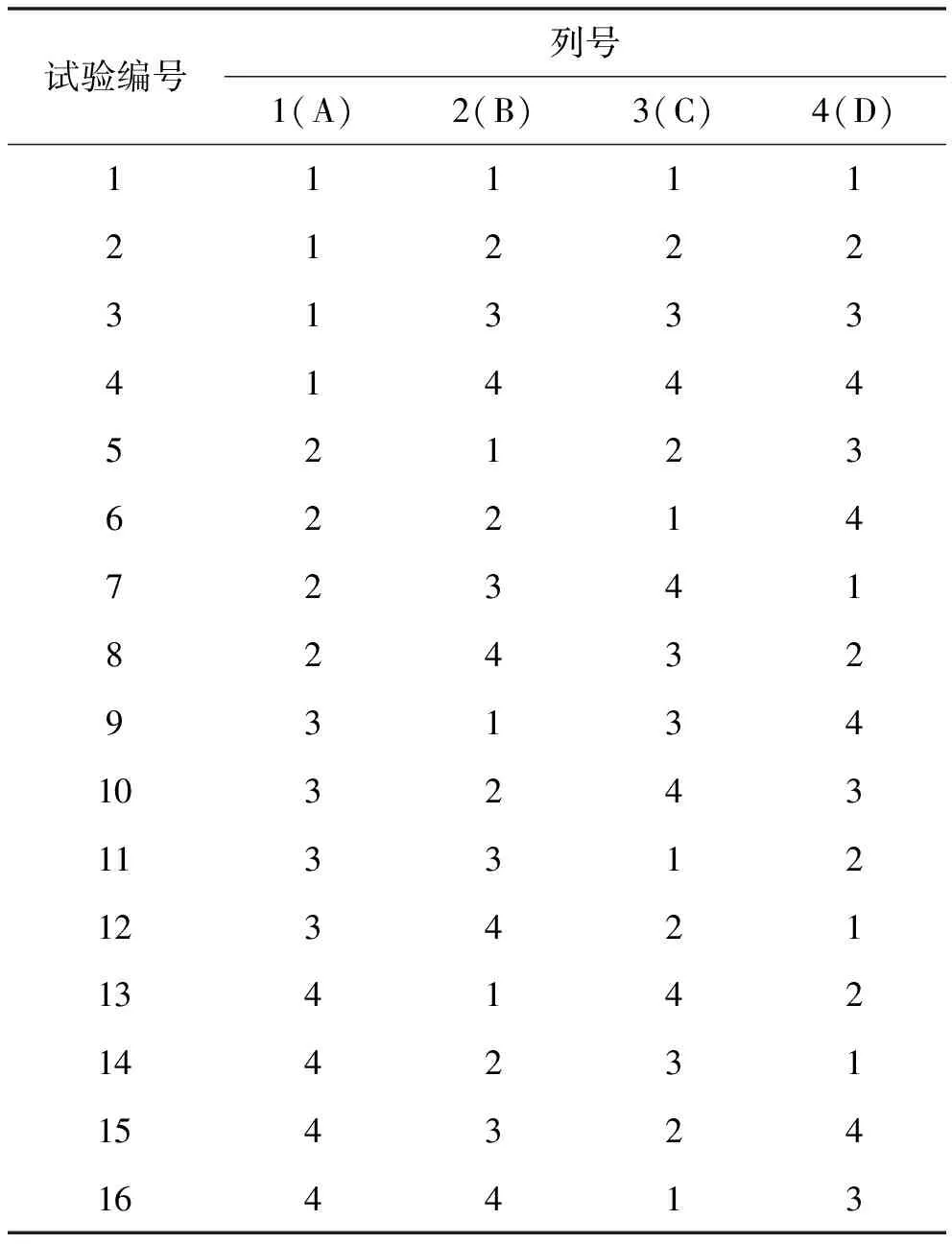
表2 正交表

3 主梁优化目标建立

为对各试验整体性能进行综合评价，该文采用公式评分法将多目标优化问题转换为单目标优化问题，即建立以主跨全截面平均应力、跨中最大挠度、混凝土数量为优化指标的综合目标函数，具体函数表达式如下：

(1)

式中：n为主跨节段数；i为主跨各节段截面编号；σsi为截面i恒活载标准值作用下上缘应力；σxi为截面i恒活载标准值作用下下缘应力；ftk为主梁C55混凝土抗拉强度标准值，ftk=2.74 MPa；f为跨中最大挠度值；[f]为挠度限值，[f]=L/600，L为主跨跨径；F为主梁总重量；G为所有试验中主梁总重量最小值；K1、K2、K3为单个目标函数；K为综合目标函数。

4 主梁优化计算结果与分析

4.1 主跨120 m主梁优化计算结果与分析

由表3可知：根据各试验的参数组合，分别建立主跨120 m各试验有限元模型，提取各试验主梁恒活载标准值作用下主跨各截面上下缘应力、跨中最大挠度及混凝土数量，按前文所述建立的综合目标函数，得主跨120 m主梁综合目标函数K计算结果如表4所示。

表3 试验参数正交表

表4 主跨120 m综合目标K计算结果

根据表4计算结果，对主梁4个试验参数进行极差及方差分析，结果见表5、6。

表5 主跨120 m综合目标K极差R分析结果

由表4可知：以最小主跨全截面平均应力为准则，主梁最优参数组合为试验4(A1B4C4D4)；以最小跨中最大挠度为准则，主梁参数组合最优为试验9(A3B1C3D4)；以最小主跨全截面平均应力、跨中最大挠度、混凝土数量构成的综合目标为准则，主梁最优参数组合为试验4(A1B4C4D4)。

此外，试验9(A3B1C3D4)、试验15(A4B3C2D4)、试验6(A2B2C1D4)分别为同一边主跨比下的最优参数组合，实际设计中可根据实际边主跨比综合考虑采用；试验12(A3B4C2D1)、试验1(A1B1C1D1)、试验14(A4B2C3D1)均为很差的参数组合，实际设计中应尽量避免使用。

由表5可知：较大的支点高跨比、较大的跨中高跨比、较小的边主跨比及合适的梁底曲线幂次对主梁综合性能有很好的改善作用。

由表6可知：支点高跨比对主梁综合性能影响显著，各试验因素影响大小顺序依次为：支点高跨比>跨中高跨比>梁底曲线幂次>边主跨比。

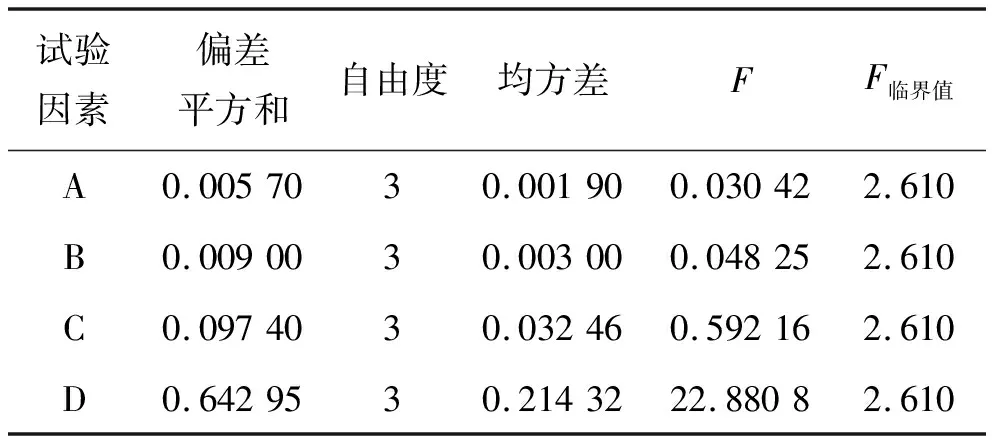
表6 主跨120 m综合目标K方差分析结果

4.2 其他跨径主梁优化计算结果与分析

在4.1节研究的基础上，根据表3各试验的参数组合，分别建立主跨100、110、130、140、150 m各试验有限元模型，分别提取各试验主梁恒活载标准值作用下主跨各截面上下缘应力、跨中最大挠度及混凝土数量，按第3节所建立的综合目标函数，得不同主跨跨径下主梁综合目标K如表7～11所示。

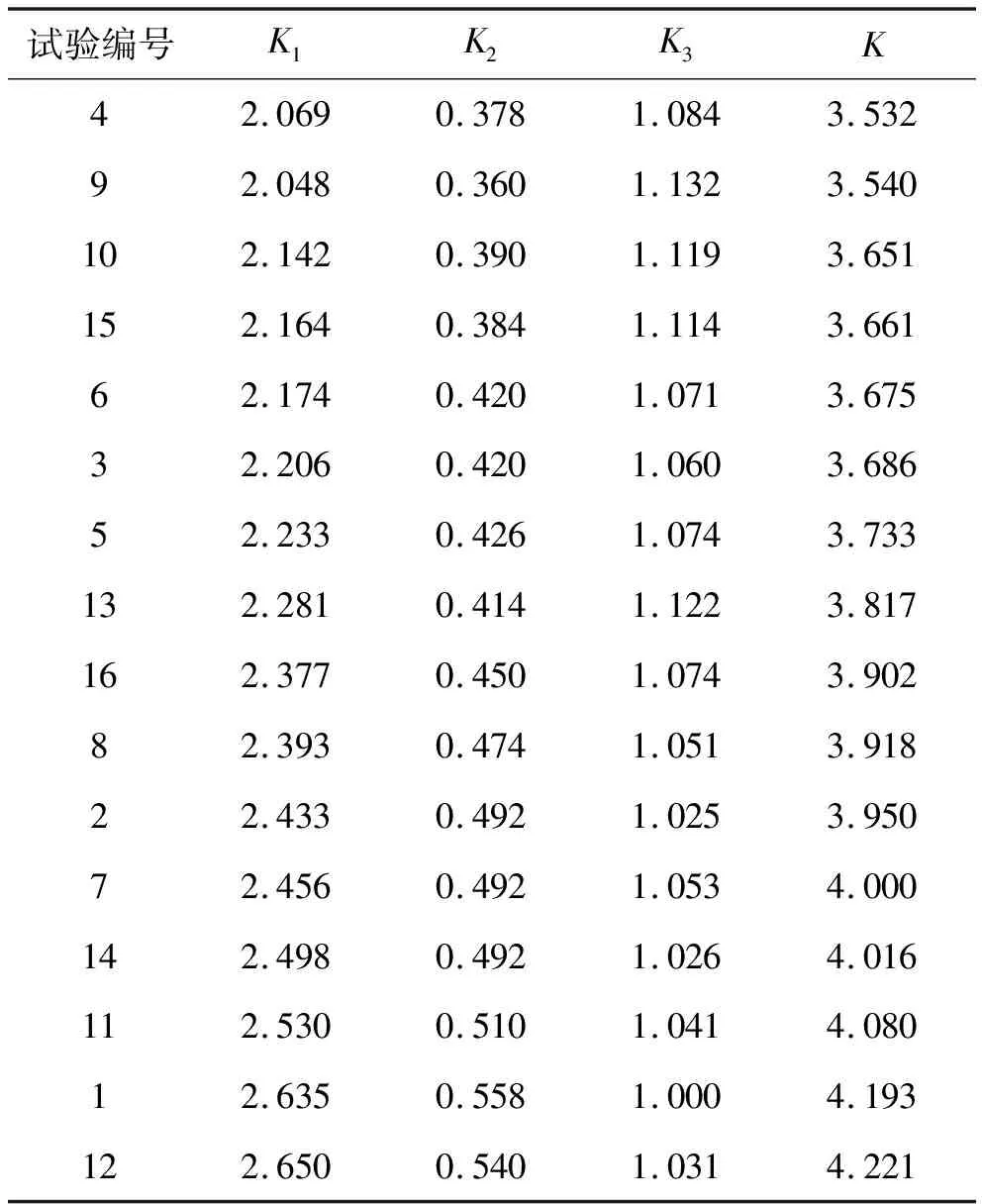
表7 主跨100 m综合目标K计算结果

表8 主跨110 m综合目标K计算结果

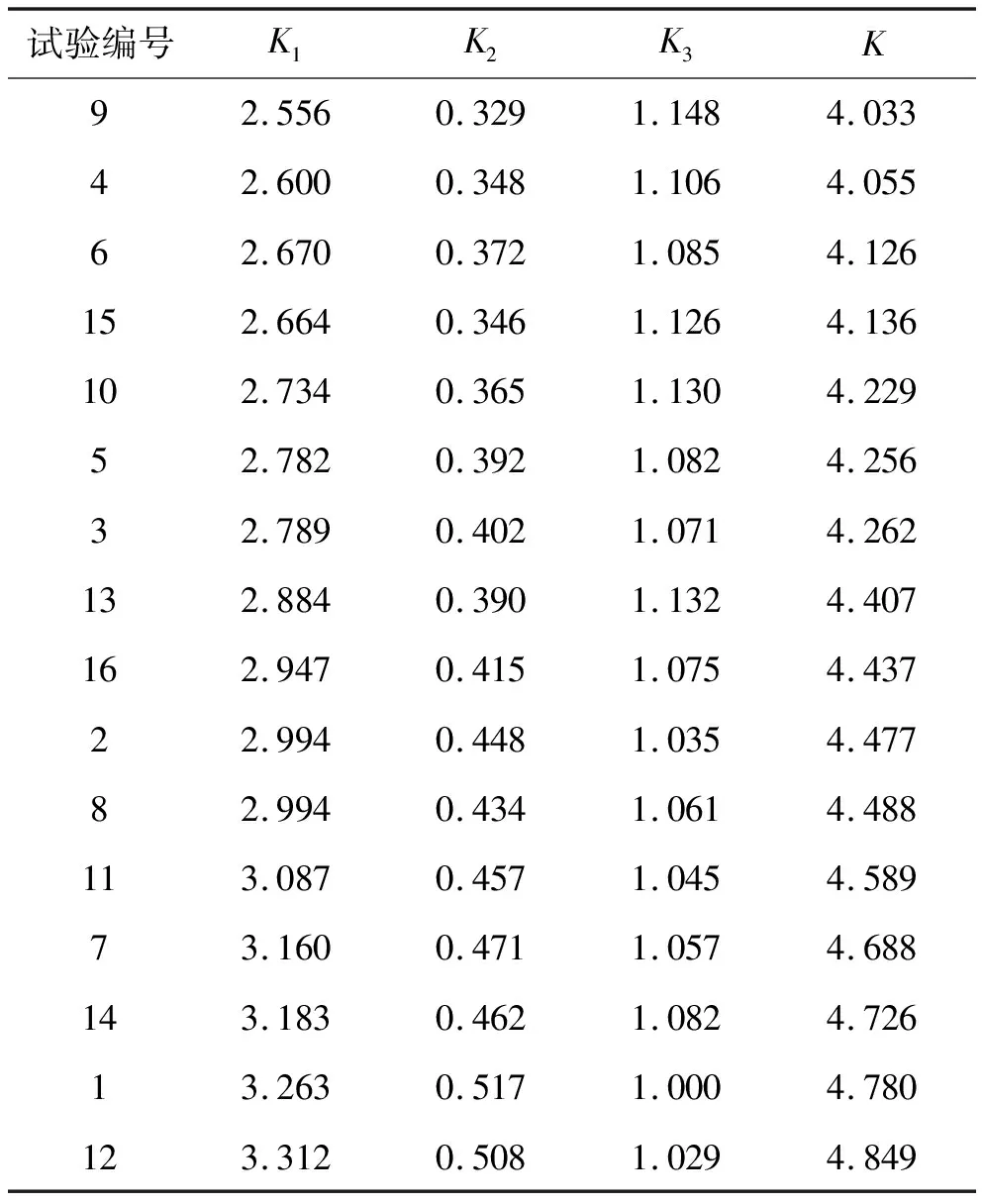
表9 主跨130 m综合目标K计算结果

表10 主跨140 m综合目标K计算结果

由表7～11可知：以主跨全截面平均应力、跨中最大挠度、混凝土数量构成的综合目标最小为准则，主梁最优参数组合基本为试验4(A1B4C4D4)[主跨130 m时，为试验9(A3B1C3D4)]，相对较优组合仍为试验9(A3B1C3D4)、试验15(A4B3C2D4)、试验6(A2B2C1D4)。

表11 主跨150 m综合目标K计算结果

相对很差组合仍为试验14(A4B2C3D1)、试验1(A1B1C1D1)、试验12(A3B4C2D1)，且其综合目标K值从小至大排序与主跨120 m也基本一致。

因此，以主跨全截面平均应力、跨中最大挠度、混凝土数量构成的综合目标最小为准则，所得主梁最优组合与最差组合具有一定的普遍性及适用性。

对以上各主跨综合目标K同样进行极差及方差分析，所得结论与主跨120 m结论基本一致，同样具有一定的普遍性及适用性

5 结论

(1)以主梁最小综合性能指标为准则，最优参数组合为A1B4C4D4，即主梁边主跨比取0.525、梁底曲线幂次取2.0、跨中高跨比取0.028 3、支点高跨比取0.066 7。

(2)实际刚构桥设计中可根据实际边主跨比考虑A1B4C4D4、A3B1C3D4、A4B3C2D4、A2B2C1D4等参数组合的综合应用。

(3)实际刚构桥设计中应尽量避免A3B4C2D1、A1B1C1D1、A4B2C3D1等综合性能很差的参数组合的应用。

(4)实际刚构桥设计中应尽量采用较大的高跨比/较小边主跨比及合适的梁底曲线幂次来改善主梁的综合性能。

(5)支点高跨比对主梁综合性能影响最为显著，各试验因素影响大小顺序依次为：支点高跨比>跨中高跨比>梁底曲线幂次>边主跨比。