有效结合画图策略 构建小学数学解决问题教学模式
(湖南省常德市安乡县城东小学 湖南 常德 415600)
在小学数学教学中,解决问题的教学没有固定的模式。但不管采用何种模式,都需经历将现实问题抽象成数学问题的过程。抽象得成功与否,在很大程度上取决于学生对题意的正确理解。有一部分学生理解能力稍强,抽象水平稍高,直接通过文字阅读就能清晰地理解数量关系,构建数学模型,顺利解决问题。但也有不少学生觉得题意晦涩难懂,怎么也想不清楚,弄不明白。当我们把抽象的数学语言、复杂的数量关系通过画一画的方式,用直观的数学图表示出来时,很多学生便豁然开朗。由此可见,画图策略是一种非常重要的分析问题和解决问题的策略。它是利用“图”的直观性来对问题中的关系与结构进行表达,以帮助学生分析问题和解决问题,从而培养学生的解决问题的能力,进而发展他们的数学思维。
小学数学解决问题教学中常采用的数学图有:示意图、线段图、数轴图、几何图等。下面,我将结合自己的教学实际,谈一谈画图策略与构建解决问题教学模式的有效结合。
1.画线段图分析数量关系
分析数量关系在解决问题过程中占有重要作用,是解决问题的根本,但是分析数量关系需要建立在对题意的正确理解的基础之上。有时,当数量关系变得复杂难以捕捉到的时候,可以对照已知条件和问题画出线段图,能很好地帮助学生理解题意,分析数量关系,化难为易,解决问题。例如五年级上册的《列方程解决相遇问题》(如图1),教材已明确提出“画出线段图分析数量关系”,这说明五年级学生这时应掌握画线段图的基本技能了,不仅能看懂,更要学会如何去画。教学时,教师还应培养学生主动画直观图分析复杂数量关系的意识。
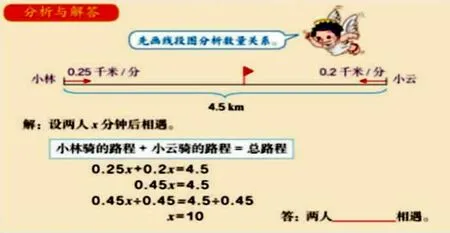
图1 画线段图分析数量关系
2.画示意图预测结果
以四年级的《烙饼》问题为例:“一口锅每次最多只能烙2张饼,两面都要烙,每面3分钟,烙3张饼至少需要多少分钟?”很多学生一开始认为是12分钟。其实不然,烙3张饼的最短时间只要9分钟。有学生上台来用学具演示操作。但操作是动态的,短短的一瞬间,有学生还没看清是怎么回事,操作就结束了。台下有学生感觉真的是一头雾水。那如何把操作的过程定格下来?让每一次烙饼的情形清晰地再现在学生的眼前?我安排了画出烙饼过程示意图的教学环节,通过画图,学生一目了然。只需烙3次,只要9分钟。
这个案例中,借助画图把复杂的问题变得简明、形象,有助于探索解决问题的思路,预测结果,收到了很好的教学效果。
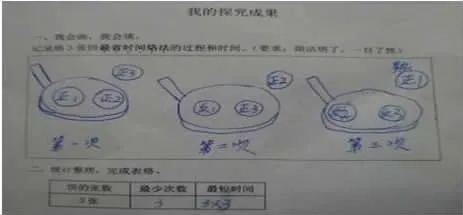
图2 烙饼过程示意图
3.画数轴图探寻规律
以“比较-和-的大小为例”(如图3)。有一部分学生对于两个数的大小关系纯靠蒙。其实,让他们在数轴上画一画,再利用“数轴上数从左到右的顺序就是数从小到大的排列”的规律轻松解决。接着再让他们结合数轴图,归纳出两个同分子负分数大小比较的方法,就比之前容易多了。
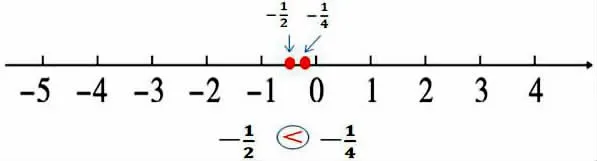
图3 数轴图
4.画几何图解释算理
几何图可以帮助学生直观地理解数学,在整个数学学习的过程中都发挥着重要作用。教学《同分母分数加减法》时,我引导学生画出几何图(如图4),并要求他们结合计算过程,抽象出计算方法。然后,再结合几何图说明和解释算理,从而达到深化算理、强化算法的目的。长期坚持不懈地训练,能促进学生敏锐的洞察力与良好数学素养的养成。
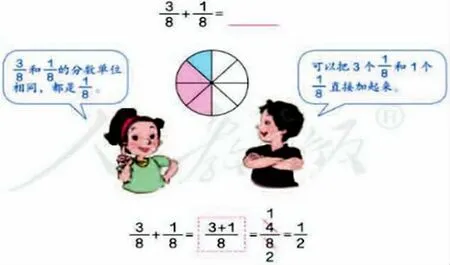
图4 几何图
结语
总之,画图策略通过数学图把抽象问题具体化、直观化,达到使学生正确理解题意,解决问题的目的。在解决问题的教学中,教师需根据实际需要、学生的知识经验、思维发展水平,逐步培养学生运用画图策略来解决问题的意识和能力。鼓励学生在解决实际问题中要将画图策略与其它策略有机结合,体验解题策略的多样性,从而构建小学数学解决问题教学的有效新模式。

