株距法的森林蓄积量抽样技术
俞维贤 徐 乐 徐长利
(1.原黑龙江省林业勘察设计院,黑龙江 哈尔滨 150001;2.黑龙江省森林植物园,黑龙江 哈尔滨 150001;3.黑龙江省林业监测规划院,黑龙江 哈尔滨 150001)
模拟株距法Kij=a(j)b=1.0306(j)-0.6306的方程式是对天然林分及自然竞争后的人工林分,林木空间正方形分布格局规律的科学表述。通过实践验证具有很强的真实性、普遍性和准确性。
样本平均胸径值通过t检验,假设成立,与总体平均直径无显著差异,估计值为无偏估计值。样本平均胸径查材积表所得样本平均单材积与1/2株距平均值推算出每公顷株数相乘,获得森林蓄积量,是精度高成本低、空间平衡性好、适应性强的森林抽样技术。
1 材料来源
材料先后于1979年、1980年、2010年、2017年在黑龙江省的依兰县、庆安县和嫩江地区及浙江省永嘉县等地的过伐林和次生林林分中进行过林分模拟株距法的抽样试验及资料的收集。
2 抽样方法
2.1 样本单元数的确定
按常规公式:n=计算样本单元数。根据依兰县先锋林场黑瞎窖104.8hm2全林实测资料,c为30%-50%;e取10%-20%;t为可靠性指标,根据样本大小查表确定。
2.2 样点调查
株距法样点调查比较简单,即野外调查时,按样点至最近1-10株样木距离由近至远顺序量测并记载其样木序号(j=1、2、3……10);水平距离(样点至样木轴心的位置,精确至0.01m)、树种名称、胸径(2cm括约)。样本单元见图1所示。
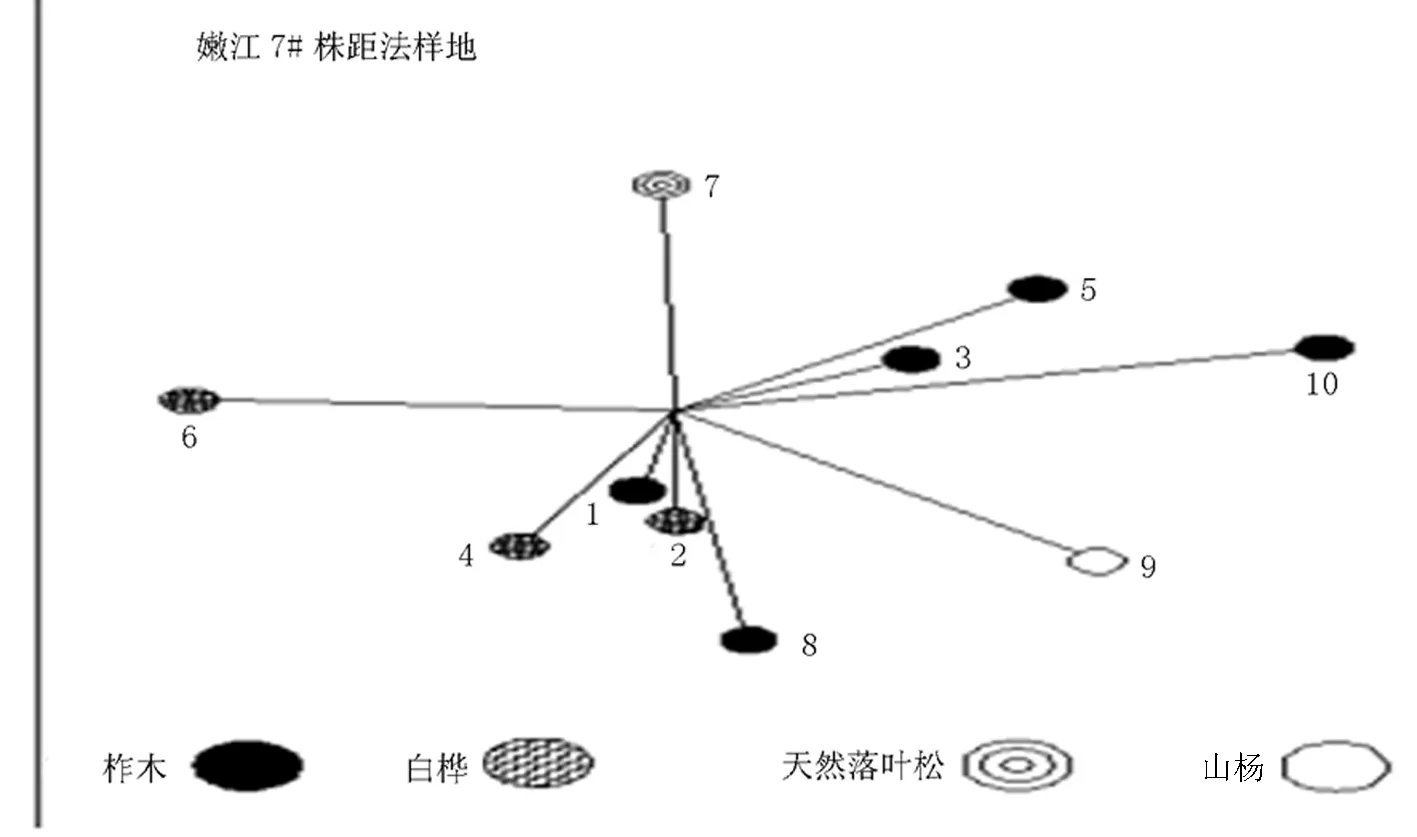
图1 嫩江县0.06hm2固定样地株距法样地套设图Fig.1 Sample Plot Layout Figure of 0.06hm2 Fixed Sample Plot in Nenjiang County By Simulated Plant Spacing Method
3 基本原理
森林是一个有生命的群体。通过充分的竞争,其株距分布具有既定的规律。笔者经过实际调查验证认为林木株距呈正方形格局分布。这种规律也不排除经过自然竞争后的人工林分。
3.1 KJ值方程表达式的建立
1)在正方形分布格局的模拟林中,随机或机械系统抽取n个样点,以样点为“0”至最近第一株样木的距离为基准株距,用“0-1”表示,并分别被样点“0至最近1-10”株的距离除,得出10个株距比值,为理论KJ值(其中KJ的下标J=1,2,3…10)。通过KJ与J方程的建立,推导出模拟株距法KJ方程的表达式:
KJ=a(j)b=1.0306(j)-0.6306
2)上述方程表达式即模拟株距法实测样点至最近1-10株样木距离换算株距的系数。通过验证换算得到的1/2株距,经推算出的单位估测株数与实际相符[1]。
3.2 模拟株距法KJ值方程表达式的应用
用计算式表示:
rij=lij×kij=lij×1.0306(j)-0.6303
式中:rij—某样点至最近1-10株样木的某株自身的1/2株距,(正方形的1/2边长)。
lij—某样点至最近1-10株样木的某株距离。
例:先锋林场第二套样本42号样点至第7株样木轴心的水平距离为9.5m。求第7株样木自身1/2的株距为:
ri.7=9.5m(1.0306×(7)^-0.6306=2.87m
4 样本的主要计算式
1)每株样木1/2平均株距计算 :
rij=lij×kij=lij×1.0306(j)-0.6303
2)样本单元1/2平均株距计算:
3)样本1/2平均株距计算:
4)样本1/2平均株距标准差计算:
5)样本1/2平均株距标准误计算:
6)样本单元平均胸径计算:
式中j=1、2、3、……10株样木数。
7)样本平均胸径计算:
8)样本平均胸径标准差计算:
9)样本平均胸径标准误计算:
10)样本每公顷株数计算:
11)样本平均胸径单株木材积计算:
式中:n—某组成树种样木株数
Vi—某组成树种样本平均直径单材积(查材积表)
M—样本总株数
12)样本平均单材积的形高计算:
13)样本平均每公顷蓄积估计值计算:
14)样本平均每公顷蓄积估计值标准误计算:
5 平均胸径t值检验
利用总体四套样本平均胸径估计值检验是否为同一总体无偏估测值。
假设检验u=u0总体实际平均胸径u0=0.2686m、四套样本平均胸径u=0.2680m、s=0.003637
经计算|t|=0.3299
查t分布表自由度 N=n-1=4-1=3 T0.05=3.18
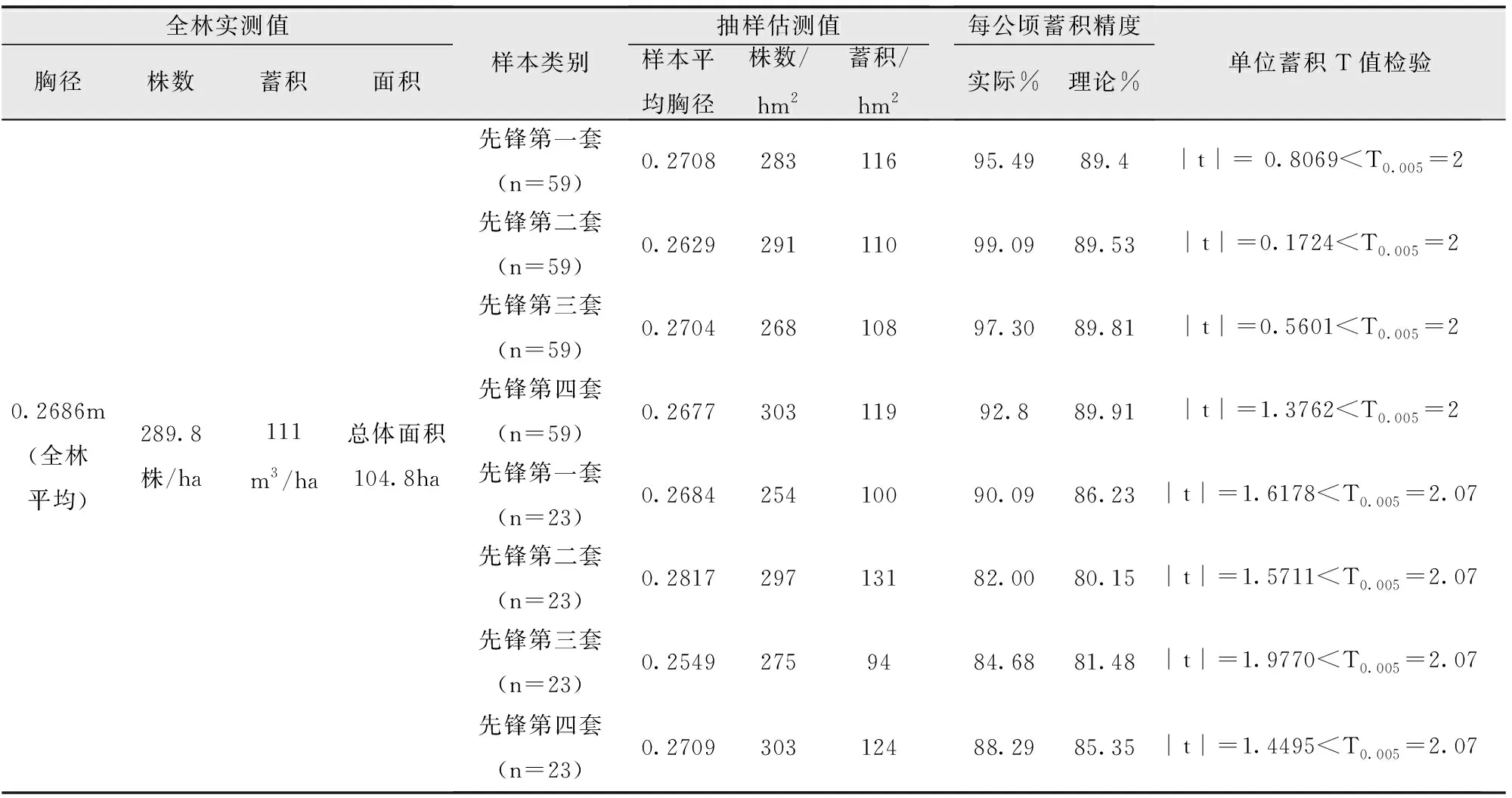
∵|t|= 0.3299 经上述计算与检验得出结论,四套样本平均胸径与总体平均胸径无显著差异。假设成立,四套样本出于同一总体,估计值为无偏估计值。 以先锋林场第二套样本为例,进行样本蓄积量估计值及精度计算。 样本特征数值见表1。 表1 先锋林场第二套株距法样本特征数表Tab.1 The Second Set of Sample Characteristics Table of Plant Spacing Method in Xianfeng Forest Farm =110.31m3≈110m3/ha =5.7564m3 以每公顷估测值进行先锋林场黑瞎窑总体内部模拟株距法抽样精度比较。 表1中,总体内的抽样精度比较表中n=59与n=23的各四套样本,实际精度均高于理论精度,经计算出的|t|值均小于查表(T0.05) ,说明抽样理论精度可靠,估测数据可信。 根据1980《林业科学》2期《关于全距模拟样地抽样调查法的效率与精度问题的商榷》一文中,当年在先锋林场104hm2与本次相同总体的工作效率的统计资料数据,结合本次模拟株距法的数据与常规系统的有边样地进行效率比较(表2)。 表2 先锋林场黑瞎窑总体内部模拟株距法抽样精度比较表Tab.2 Comparison Table of Sampling Accuracy of Plant Spacing Method for Overall Internal Simulation of Heixiayao in Xianfeng Forest Farm 表3 常规有边样地与模拟株距法样点工作效率比较表Tab.3 Comparison Table of Work Efficiency between Conventional Edge Plot and Simulated Plant Spacing Plot 根据表3数据分析,模拟株距法样点是常规有边系统样地(0.06ha)的效率18倍(即5.5小时比100小时)。 以1980年庆安县大青山林场调查资料为参考数据(表4)。 表4 林场为总体的蓄积量估测比较表Tab.4 Comparison Table of Total Volume Estimation of Forest Farm 1)模拟株距法Kij=a(j)b=1.0306(j)-0.6306的方程式是对天然林分,林木空间自然分布规律的科学表述。通过实践验证具有很强的真实性、普遍性和准确性[1]。 2)样本平均胸径均通过T检验,四套样本平均胸径与总体平均胸径无显著差异,假设成立。估计值为无偏估计值。 4)通过八套样本的精度分析与值检验,可以肯定模拟株距法抽样精度可靠,估测数据可信。 5)无边样地的抽样关键决定于林分株数的测定,模拟株距法经过验证在单位面积的株数测定上,比日本西泽正久“距离法”、F.科克斯“顺序法”均居于优势。 6)模拟株距法森林蓄积量抽样工作效率是0.06hm2有边样地的18倍。是高效低成本、空间平衡性好,适应性强的森林抽样技术。6 样本蓄积量估计值及精度
6.1 样本特征数

6.2 样本每公顷蓄积量估计值
6.3 每公顷蓄积量估计值的标准误
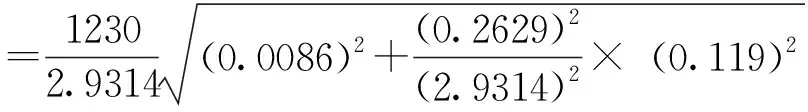
6.4 每公顷蓄积量估计值精度
6.5 模拟株距法蓄积量估计值的实际精度
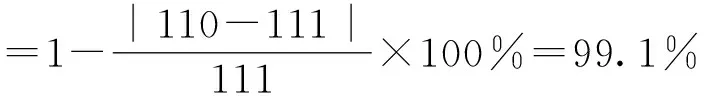
7 模拟株距法的效率比较
7.1 实测总体内部的精度比较
7.2 实测总体内部的效率比较

7.3 林场为总体的蓄积量估测比较

8 结论


