倾斜来流下圆管的稳定性及响应分析
卢 佳, 鲁 丽
(西南交通大学力学与工程学院, 成都 610031)
引 言
作为反应堆中重要组件之一,热交换器的换热管具有轻薄易失效的特点[1],是反应堆能安全运行的重要保障,类似的圆管体或管束结构也广泛应用于工业中,例如海洋立管以及拖拽式声呐,故而其流致振动问题向来是学术界关注的热点问题之一。流致振动破坏机理有多种,其中破坏性最强的为流体弹性不稳定导致的振动[2],即湍流或其他原因引起的管阵中某根圆管的位移使流场发生变化,又导致阵中其他圆管的振动。随着流速增加,结构不断从流体吸收能量并持续振动,在一定流速下,管体吸收能量大于结构耗散能量,结构的动力学响应会突然增大,发生大幅振动[3]。
流体弹性不稳定性是导致结构失稳的主要原因,故其成为流致振动问题的重点,数十年来,学者们已对此做过大量的工作。Chen和Cai使用非稳态模型对带有松动支承的简支圆管进行了稳定性和响应分析[4]。Price和Paidousis提出了准稳态模型并对中点处有间隙支承的固支管进行了动力学分析[5]。黄平系统地讨论了直管管束和U型管排的流体弹性不稳定性、非有效支承对流体弹性不稳定的影响和管束湍流诱发振动问题[6]。李云东考虑到圆柱横向变形引起的附加轴力和热荷载的影响,对横向流中单弹性圆管体的热弹性颤振进行了研究[7]。Tan等使用ANSYS软件进行仿真,研究了节径比和管间相位滞后对系统振动特性的影响,探讨了系统发生流弹失稳的作用机理[8]。
近年来理论模型的建立也有很大发展,姜乃斌等基于Yetsir和Weaver的模型,修正了前人的参数,提出一种非定常半解析模型,并用多管单元模型对几种不同排列的管阵进行了流弹失稳分析[9]。Vilas Shinde等考虑了排列方式、节径比和雷诺数的影响,提出了一种新的理论模型,该模型能较好地捕捉到系统不稳定边界的跳跃现象以及系统的多个稳定区域[10]。
除数值计算外,实验也是学者们研究管阵振动的高效手段,Lai等通过实验研究了两相横流作用下管阵的流弹失稳现象,并推导了临界流速的计算公式[11]。Tan等研究了转置三角形排列管阵的流弹失稳现象,得到一系列有意义的结果[12]。
前人关于管束振动研究多为针对来流方向与结构轴向垂直的横向流,或是二者方向一致的轴向流,但在实际工程应用中,管柱结构与来流方向并非完全垂直或一致,往往存在一定角度(如管壳式换热器、海洋立管等),这样的来流被称为倾斜流。研究者通过一系列实验和理论验证发现,当倾斜角比较小时,可以忽略流体平行于管子轴线的流速分量,仅通过正交于圆管轴线的流速分量就能比较精确地预测结构的力学特性,这项原理称为独立性原理(IP)或余弦法则。虽然各个研究者给出的有效范围各不相同,但普遍认同当倾斜角小于40°独立性原理是适用的。当倾斜角大于40°,体轴向分量对结构的影响比较明显,不适用于独立性原理[13-14]。Lucor验证了圆柱受倾斜流影响时独立性原理的可靠性[15]。Jain针对倾斜刚性圆管的涡激振动进行了一系列实验[16]。及春宁等开展了海洋立管时受倾斜流作用下的涡激振动现象[17],进一步探讨了独立性原则的适用范围,并研究了涡激振动时立管的尾涡结构。总的来说,这方面的研究成果不算丰富,而关于倾斜流下圆管的流弹失稳研究也比较少。
基于以上研究现状,为了研究来流方向与管柱结构存在倾斜夹角的倾斜流对管束振动的影响,本文以方形排列刚性管阵中的单根柔性圆管为研究对象,并考虑圆管中点处存在因松动产生间隙的支承,在振幅较大时,圆管与支承相碰撞产生非线性力的状况,采用立方弹簧非线性模拟碰撞力,通过数值计算方法研究其在倾斜流作用下的流弹失稳现象。
1 动力学模型及方程
设倾斜角α为来流方向与圆管横截面之间的夹角,如图1(a)所示。建立圆管体的物理模型如图1(b)所示。

图1 力学模型
根据梁的振动理论将圆管体简化为欧拉梁,并将来流分解为沿x、y两个方向的分量。为方便计算,本文将圆管简化为一根欧拉-伯努利梁,通过微元法建立系统结构控制方程:
(1)
其中,EI为圆管体的弯曲刚度;w为圆管沿z即垂直于来流平面方向的位移;x为沿圆管体长度方向的位置坐标;c代表阻尼系数;m为圆管体的单位长度质量;F1为流体沿y轴流动的分量引起的使圆管在z方向振动的横向流流体力,其表达式由Price和Paidoussis在文献[18]中给出:
(2)
式中:U表示y轴方向的流体分量;ρ表示流体密度及速度;CD表示流体的阻力和升力系数;D为圆管直径;Cma表示流体的附加质量系数;t表示结构运动与流体动压之间的时滞。
F2为流体沿x轴流动的分量引起的使圆管在z方向振动的轴向流流体力,基于细长体理论,文献[19]给出其表达式:
(3)
其中,v表示x方向的流体分量。设f(w)为圆管体在松动约束作用下振动时的碰撞力,采用立方弹簧非线性模型进行模拟,则表示为:
(4)
引入无量纲参数:
(5)
将无量纲参数代入式(1)中,得到系统无量纲运动方程:
(6)
其中,λ1的第一阶无量纲特征值。
2 方程离散
使用伽辽金法对方程(6)进行离散:设梁的模态函数为φi(ξ),方程(6)中的位移函数写成:
(7)
取梁的前四阶模态,将式(7)代入方程(6),在方程两端同乘φi(ξ),并在[0,1]上积分,得到:
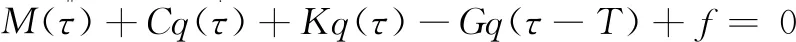
(8)
其中:
(9)
对于本文所研究的固支梁,其模态函数表示为:
φi(ξ)=cosβiξ-chβiξ-σi(sinβiξ-shβiξ)
(10)
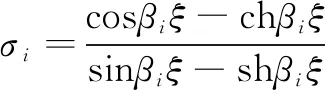
根据振动力学原理,对于本文所研究的固支梁,其前四阶特征根分别为:
β1=4.730041,β2=7.85305,β3=10.995608,β4=14.137166
(11)
3 系统稳定性分析
首先将系统扩维降阶:
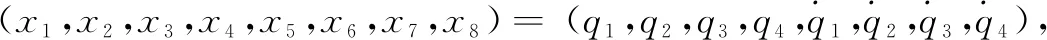
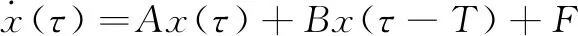
(12)
其中:
(13)
对线性系统进行分析,消去F得到:
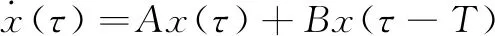
(14)
设式(14)的解为:x=V0eσ+iwτ当σ<0时,系统渐进稳定,σ>0,系统状态不稳定,σ=0为临界状态,将σ=0代入式(14),得到特征方程:
|A+Be-iwτ-iwI|=0
(15)
求解式(15)即可计算出系统的临界流速Ucr以及临界频率wcr,本文取系统前两阶模态进行计算,圆柱节径比为1.5,其余系统参数如下:
(16)
求解出系统临界流速及频率见表1。

表1 α=60°统的无量纲临界流速和频率
为观察系统参数对临界流速的影响,给出不同倾斜角的系统临界流速见表2。
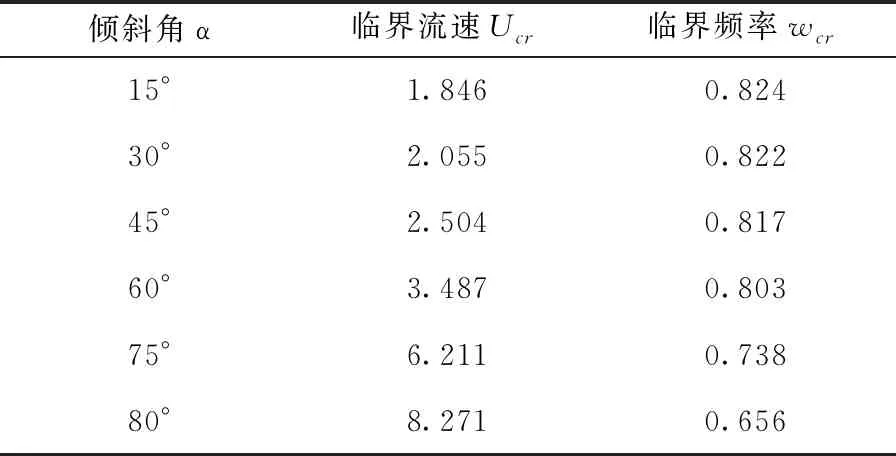
表2 不同倾斜角下系统的无量纲临界流速和频率
由表2可见,随着倾斜角α增加,系统的临界流速不断增大,且增长速率也呈增大的趋势,在海洋管道、拖拽式圆管等涉及轴向流中圆柱体的实际工程计算中,应考虑有倾斜角来流对临界流速的影响。
4 非线性响应分析

图2~图6给出了当倾斜角等于60°时,系统在各个流速下的响应相图及时程曲线。计算结果表明,随着流速增加,当无量纲流速U<3.50,系统保持稳定运动;当U=3.50,系统出现颤振失稳,这与第3节中通过线性系统预测的临界流速Ucr=3.487吻合较好,其响应相图如图2(a)所示,其时程曲线如图2(b)所示,可以看出系统的振动幅值在时间历程中保持不变。
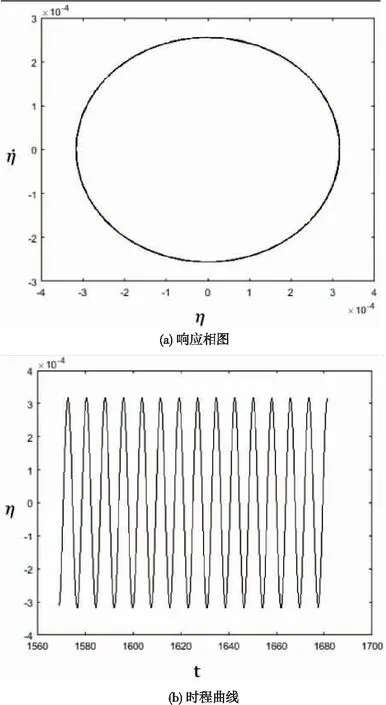
图2 U=3.50系统响应
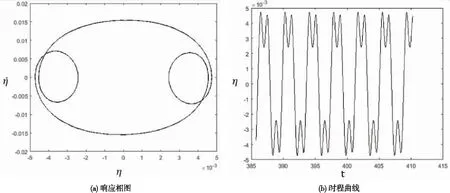
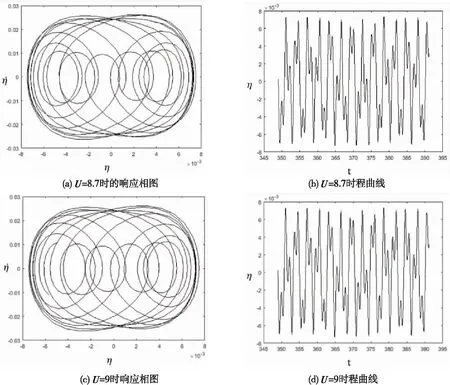
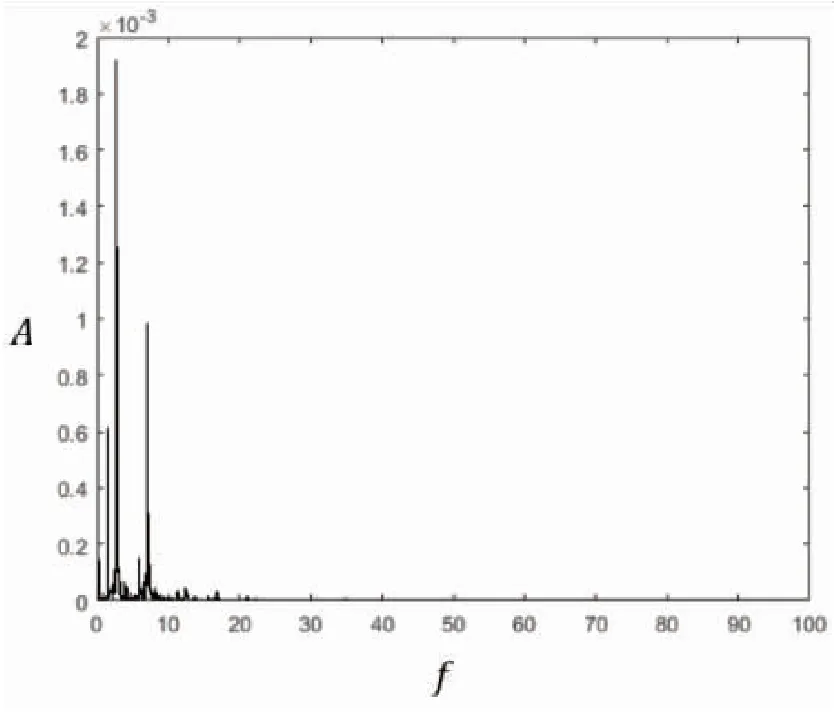
当3.50 图3 U=5时的系统响应 当流速在6.2 图4 U=7.50时系统的响应 当流速在8.3 图5 U=8.7系统响应 图6 U=9系统的幅频曲线 以上计算结果显示,本文所选参数下,随着流速不断增加,系统依次发生了极限环运动、周期1振荡运动以及拟周期运动。对比文献[18]中的模型,在具有相同的非线性力以及系统参数的状况下,圆管受到与管子轴线正交的横向流作用时,系统最终进入混沌状态,但在本文所研究倾斜角α=60°斜流作用下,系统没有发生混沌现象,可以发现倾斜角的存在对于系统响应形态有所影响,且横向流体的运动对系统非线性动力学的影响较大。 本文研究了在倾斜来流和松动支承共同作用下的两端固支圆管的动力学行为,包括稳定性分析及非线性系统响应分析,采用三次弹簧力模拟了圆管发生碰撞时受到的非线性力。随着来流倾斜角从0°增加到90°,系统临界流速不断增大,且增长速率也在提升,倾斜角大小对系统临界流速的影响较大,且相较于平行圆管轴线方向的来流,与圆管轴线相垂直的来流对系统临界流速的影响更明显,证明目前在管壳式换热器等圆管结构受到横向流冲刷的工程计算中,不考虑流体倾斜角的做法是保守、合理的。当倾斜角为60°时,流速达到第一阶临界流速后,系统发生颤振失稳,随着流速不断增加,系统振动幅值亦不断增大,依次出现极限环、周期1振荡运动和拟周期运动,并未出现混沌运动,倾斜角的存在对系统响应形态有影响。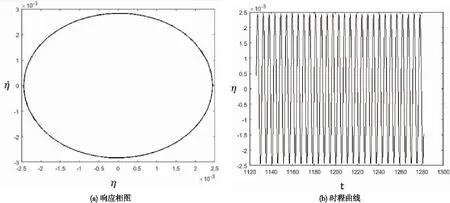
5 结束语

