关于L-半拓扑空间中连续性和分离性的探究

李 飞， 朱培勇

(电子科技大学数学科学院， 成都 611731)

引 言

2002年，匈牙利数学家A.Csaszar在文献[1]中引入广义拓扑的概念并且得到基本结果之后，文献[2-9]对广义拓扑进行了一些较为深入研究，得到了广义拓扑空间上的一些点集性质、广义拓扑基的性质、映射性质、广义拓扑的比较等一系列结果。由于广义拓扑概念仅包含拓扑概念中三个条件的一半，即广义拓扑实际上是一个“半拓扑”。2015年，文献[10]把广义拓扑重新命名为上半拓扑，引入了下半拓扑的概念并且类比拓扑空间的基本性质，在下半拓扑空间上获得了一些基本的点集性质。以此同时，文献[11]和文献[12]利用文献[10]的方法，

将拓扑进行重新剖分成两个新的半拓扑：左半拓扑与右半拓扑。文献[12]和文献[13]主要对右半拓扑空间的点集理论与网收敛性质进行研究，得到了一些关于闭包、子空间、分离性和网收敛方面的一列结果。在此，人们自然会问：

问题：左半拓扑空间是否具有类似于右半拓扑空间的上述一系列研究结果？

文献[11]和文献[14]就上述问题进行研究，在左半拓扑(L-半拓扑)空间上得到了一些关于基本点集(邻域、开集、闭集、闭包、子空间)与网收敛等方面的一些结果。本文，首先对文献[11]的子空间性质与开集性质进行补充，用一个例子说明L-半拓扑空间中关于开集的一个结果；然后讨论L-半拓扑空间上映射的连续性以及点集的分离性质。

1 预备知识

首先给出L-半拓扑空间中的定义以及相关概念。

定义1[11]设X是任一非空集合，δ是X的一些子集构成的集族，如果下列条件被满足:

(1)X∈δ。

(2)若Gλ∈δ(λ∈Λ)，则∪λ∈ΛGλ∈δ(其中Λ为任意指标集)。则称δ为集合X的L-半拓扑，并且称有序偶(X,δ)为一个L-半拓扑空间，集族δ中的每一个集合都称为L-半拓扑空间(X,δ)的L-开集。

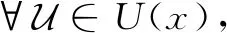
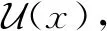
类比拓扑学(参考文献[15])中相应概念，引入L-半拓扑中如下一些概念。

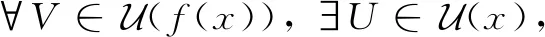
定义6设Χ，Y为两个L-半拓扑空间，f：X→Y是一个一一对应，如果f：X→Y与f-1：Y→X都L-连续，则称映射f：X→Y为一个L-同胚映射。

定义7设Χ为L-半拓扑空间，在同映射下保持不变的性质称为L-半拓扑不变性质。

定义8设(Χ,δ)是一个L-半拓扑空间。

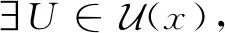
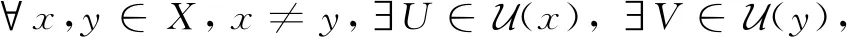
定义9设(Χ,δ)是一个L-半拓扑空间。

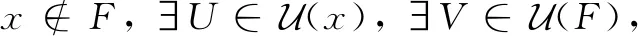
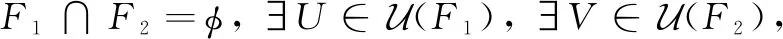
定义10设(Χ,δ)是一个L-半拓扑空间，L-半拓扑空间Χ称为L-完全正则空间，如果对于Χ中任何闭集F以及任何x∈XF，存在L-连续映射f：X→[0,1]，使得f(x)=0且f(F)⊂{1}。

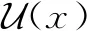
定义12设(X,δ)为L-半拓扑空间，L-半拓扑空间X称为L-A1空间，对于∀x∈X，点x有一个至多可数的L-邻域基。

定义13设(X,δ)为L-半拓扑空间，L-半拓扑空间X称为L-A2空间，如果X有一个至多可数的L-半拓扑基。

此外，本文中涉及到的概念、术语和记号，如果没有特殊申明，都来自于文献[15]。

2 L-半拓扑空间中的基本点集性质

定理1设(X,δ)为L-半拓扑空间，A⊂Y⊂X，则：

(1)Y是X的L-闭集，则A是X的L-闭集当且仅当A是Y的L-闭集。

(2)Y是X的L-开集，若A是X的L-开集，那么A是Y的L-开集。反之结论不成立。

证明(1)(必要性)A闭于X，则A∩Y闭于Y，而A∩Y=A,因此A闭于Y。

(充分性)设A闭于Y，由文献[11]定理2.6(1)可知，存在X中闭集F使得A=F∩Y,又因Y是X中闭集，由文献[11]定理2.2(LF2)可知F∩Y是X中闭集，故A闭于X。

(2) 因为A开于X，则A∩Y开于Y，又A⊂Y，则A∩Y=A，因此A开于Y。

反之，取X={a,b,c},δ={{a,b},{b,c},X}，Y={a,b}，A={b}，则A⊂Y⊂X，显然Y是X中的L-开集，A是Y中的L-开集，但A不是X中的L-开集。

定理2设(X,δ)为L-半拓扑空间，A⊂Y⊂X，有intX(A)≠intY(A)∩intX(Y)。

证明取X={a,b,c},δ={{a,b},{b,c},X}并且Y={b,c},A={b},则intX(A)=φ,intY(A)={b},intX(Y)={b,c}，所以,intY(A)∩intX(Y)={b}。进而，intX(A)≠intY(A)∩intX(Y)。

3 L-半拓扑空间上的连续映射和同胚映射

为了给出L-连续映射的等价刻画，先引入L-邻域基和L-邻域子基的概念：

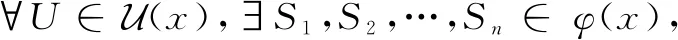
在此，关于L-连续映射有如下等价刻画：

定理3设Χ与Y都是L-半拓扑空间，f:X→Y，x∈X，则下列三个命题等价：

(1)f在点x处L-连续。

(2)点f(x)有一个L-邻域基νf(x)，使得∀V∈νf(x)，有f-1(V)∈U(x)。

(3)点f(x)有一个L-邻域子基Wf(x)，使得∀W∈Wf(x),有f-1(W)∈U(x)。

证明采用(1)⟹(2)⟹(3)⟹(1)的顺序进行证明。

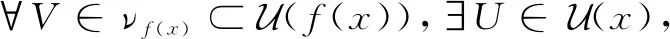
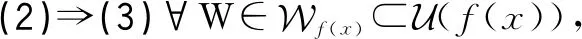
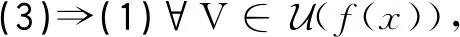
定理4若f:X→Y和g:Y→Z均为L-连续映射，则复合映射g∘f:X→Z也是L-连续映射。

证明 设G开于Z，因为g:Y→Z为L-连续，故g-1(G)开于Y，又因为f:X→Y为L-连续，故g∘f-1G=f-1(g-1(G))开于X，故g∘f是L-连续。

定理5邻域、内点、闭包都具有L-半拓扑不变性质。

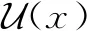
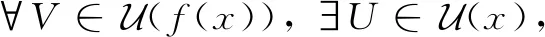
(2)再证内点具有L-半拓扑不变性质。

设A⊂X，f：X→Y是一个L-同胚映射，则f(A0)=(f(A))0。

事实上，∀x∈A0，存在G开于X使得x∈G⊂A，则f(x)∈f(G)⊂f(A)。因为f:X→Y是L-同胚，则f(G)开于Y，所以，f(x)∈(f(A))0。即f(A0)⊂(f(A))0。

反过来，∀y∈(f(A))0，存在W开于Y使得y∈W⊂f(A)，则f-1(y)⊂f-1(W)⊂f-1f(A)=A。因此f-1(y)⊂f-1(W)⊂A0，故y∈W⊂f(A0)，所以(f(A))0⊂f(A0)，从而，f(A0)=(f(A))0。

(3) 下证闭包具有L-半拓扑不变性质。

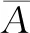
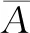
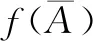
4 L-半拓扑空间中的分离性质

在L-半拓扑空间中，L-T0空间、L-T1空间和L-T2空间三者之间有如下关系。

定理6存在L-T0空间不是L-T1空间，也存在L-T1空间不是L-T2空间。

证明(1)先证L-T0⟹L-T1。

取X={a,b,c}，δ={{a,b},{a,c},X}，显然X是L-T0空间，然而对于点a,b而言，含b的L-开集必含有a，所以X不是L-T1空间。

再证L-T1⟹L-T2。

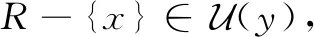
L-半拓扑空间中L-T1空间和L-T2空间有如下两个等价条件。

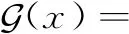
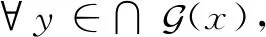
(充分性)反证若X不是L-T1空间，则∀x,y∈X,x≠y,则∀U∈U(x),有y∈U,则y∈b,c∩G(x)，又∩G(x)={x}，则y∈{x}，这与x≠y矛盾，则X是L-T1空间。

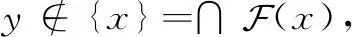
在一般拓扑空间中有(参考文献[15])：(1)T1空间的任意有限子集的导集是空集。(2)X为T1空间，A⊂X，则A的导集必为闭集。但在L-半拓扑空间中，上述两个结论不成立。

例1取X={a,b,c},δ={{a,b},{b,c},{a,c},X}，则X为L-T1空间，再取X中任一有限子集A={a,b},则A′={c}，显然A′≠φ。

例2取X={a,b,c},δ={{a,b},{b,c},{a,c},X}，则X为L-T1空间，取A={a,b,c}，则A′={a,b,c}，显然A′不是闭集。

下面是关于L-半拓扑空间中正则空间以及正规的几个相关结论。

定理9设X为L-半拓扑空间，则正则的L-T0空间是L-T2空间。

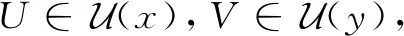
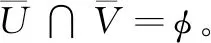
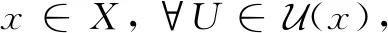
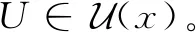
定理12设X为L-半拓扑空间，则L-正规空间X为完全L-正则空间当且仅当它是L-正则空间。

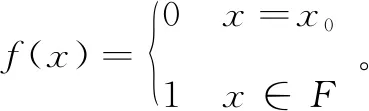
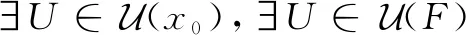
定理13设B为X的一个L-半拓扑基，则∀x∈X,Bx={B|x∈B∈B}为点x的一个L-开邻域基。

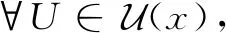
5 结束语

本文在文献[11]的基础上进一步的研究了L-半拓扑空间中的一些性质，得到了L-半拓扑空间中关于连续性和分离性的一些结果。从而，丰富了L-半拓扑空间理论。同时，给出反例说明了在拓扑空间中成立的命题而在L-半拓扑空间中不成立。