Time-Varying Asymmetrical BLFs Based Adaptive Finite-Time Neural Control of Nonlinear Systems With Full State Constraints

Lei Liu, Member, IEEE, Tingting Gao, Yan-Jun Liu, Senior Member, IEEE, and Shaocheng Tong, Senior Member, IEEE

Abstract—This paper concentrates on asymmetric barrier Lyapunov functions (ABLFs) based on finite-time adaptive neural network (NN) control methods for a class of nonlinear strict feedback systems with time-varying full state constraints. During the process of backstepping recursion, the approximation properties of NNs are exploited to address the problem of unknown internal dynamics. The ABLFs are constructed to make sure that the time-varying asymmetrical full state constraints are always satisfied. According to the Lyapunov stability and finitetime stability theory, it is proven that all the signals in the closedloop systems are uniformly ultimately bounded (UUB) and the system output is driven to track the desired signal as quickly as possible near the origin. In the meantime, in the scope of finitetime, all states are guaranteed to stay in the pre-given range.Finally, a simulation example is proposed to verify the feasibility of the developed finite time control algorithm.

I. Introduction

AFTER decades of research and development, adaptive control approach has made great progress in theory and in practical engineering applications. At the same time, as one of the most important methods to solving uncertain nonlinear systems, adaptive control has gradually become one of the hottest topics in the field of nonlinear control [1], [2].Research on nonlinear control methods have become more conducive to the application of adaptive control in aerospace,robot arm control, satellite attitude tracking control, process control, and many other industrial fields [3]–[5]. Besides, the adaptive backstepping control design technique and a systematic design method for parametric uncertain systems has been extensively proposed in the last few years. In addition, the combination of backstepping technique and adaptive NN control [6], [7] or fuzzy control [8], [9] has also made great progress in recent years.

Modern industrial processes tend to be more and more largescale and complicated, presenting a high degree of non-linearity and serious uncertainty. Moreover, due to the influence of actual mechanical devices and other indicators, constraint problems inevitably appears in real systems. If these constraints are not handled or mishandled, they easily affect the stability of the system, which may cause serious accidents. The barrier Lyapunov functions (BLFs) based constraint control method is widely used to deal with such constraint problems. Among them, many works pay close attention to nonlinear systems by describing linear-in-the-parameters condition with the state constraints, such as in [10], [11] and the references therein.Furthermore, the scheme, combining the neural networks (NNs)or fuzzy logic systems (FLSs) [12]–[14] with the backstepping technique, has been regarded as a promising way to account for uncertain nonlinear constrained systems. For example, an adaptive NN controller is designed in [15] based on BLF for a nonlinear strict feedback system with unknown driving characteristics. The BLF was applied in [16] to uncertain Euler-Lagrange systems, and the corresponding adaptive NN control approach was proposed while all state constraint conditions are satisfied. The corresponding adaptive controller was developed in [17] for special nonlinear MIMO (multiple-input and multiple-output) systems with state constraints and unknown time delay. Moreover, other results [18]–[24] studied the corresponding adaptive control problems based on the above methods. In addition, more and more scholars begin to work on the study of time-varying constraint control as a key research topic because many constraints in the practical systems are in time-varying case. Based on this, the time-varying state constraints were considered in [25], [26] to robotics and marine vessels. Meanwhile, theoretical research on nonlinear systems with time-varying constraints were also carried out in [27]–[29]and so on. However, it is known that although the control scheme studied in the above papers can ensure the stability of systems, they do not consider achieving the desired effect in a finite-time interval, which makes the systems more difficult control.

Based on the research of adaptive control theory, the concept of finite-time stability was first proposed in [30]. Finite-time control theory is widely known for their good robustness and anti-disturbance performance. The adaptive finite-time widely used in other types of constraints and systems. Therefore,in the future, we will focus on different constraints (such as Tangent type-BLF based partial state constraints) and non-strict feedback systems.

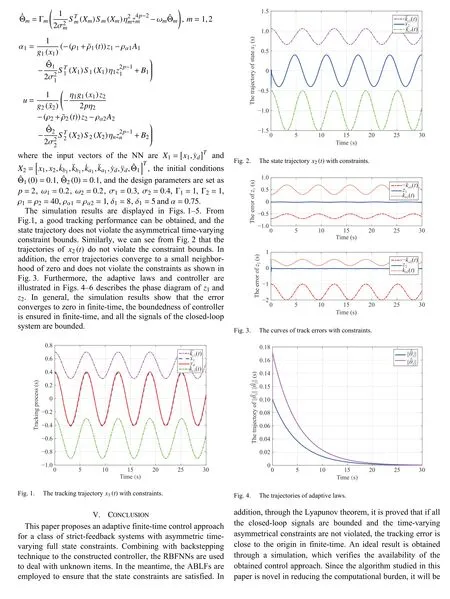
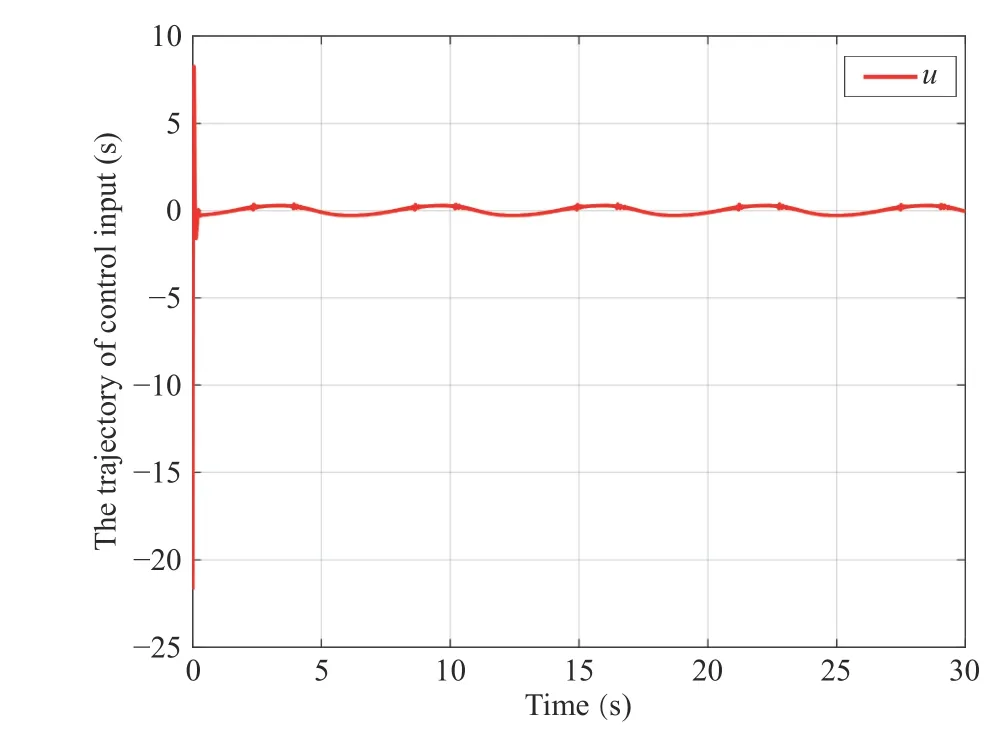
Fig.5. The controller trajectory.

Fig.6. The phase diagrams.