粘性条件下含不同导叶数的液力透平水力损失分析

毕智高 孙 琪 相玉琳 蒋文明

（1.榆林学院a.化学与化工学院； b.陕西省低变质煤洁净利用重点实验室； 2.中国石油大学储运与建筑工程学院）

离心泵是一种完全可逆式旋转机械，将它反转作液力透平使用具有结构简单、 安装方便、占地面积小、 可批量生产及运维费用低等优点［1，2］，因而广泛用于回收各种工业流程中液体工质所含的富余压能。

近年来，国内外学者对泵作透平在叶轮进口添加导叶［3～6］以改善其水力性能方面的研究不断增多。 文献［7］研究发现，添加导叶能够改善小流量工况下水力透平运行的不稳定性。 文献［8］采用数值分析的方法，发现添加导叶能优化透平内部流动、增加效率。 文献［9］研究表明，叶轮进口前添加导叶的方法可以很好地降低液力透平内的压力脉动幅值， 有助于提高透平运转的稳定性。 文献［10］研究了导叶数对多级离心泵反转式液力透平性能的影响，结果表明导叶数越少的模型内部流动越均匀。 综上可见，为液力透平增添导叶确实能够使叶轮进口环量均匀，改善透平水力性能，提高透平效率。

液力透平内工质的流动状况既依赖于各独立过流部件的形状和尺寸，又取决于所有过流部件的组合与匹配。 文献［11～14］分析了泵作透平内水力损失的分布规律，为提高透平效率和优化透平结构提供了方向。 然而，这些研究并未包含导叶这一关键部件。 同时，上述研究均以常温清水为工质，而工程实际中用于能量回收的工艺介质常处于粘性条件下，工质黏度的增大必然会对透平的性能产生影响。

为此，笔者在已有工作的基础上以不同黏度的纯液作为工质，通过对同一台离心泵反转的液力透平叶轮进口匹配不同叶片数目的导叶，应用CFD技术分析探讨粘性条件下含不同导叶数的液力透平水力损失的分布规律，为液力透平结构优化提供参考。

1 研究方案

选取一台比转速ns=41的单级单吸离心泵反转作液力透平为研究对象。 泵工况设计参数分别为： 转速n=2960r/min， 流量Q=52m3/h， 扬程H=101m，效率η=60.9%。 透平工况下，参照文献［8］的设计与改型方法， 为叶轮进口添加叶片数Z0分别为6、8、10的导叶。 包含导叶后液力透平的主要

几何参数如下：

叶轮 进口直径 68mm

出口直径 285mm

叶片出口安放角 30°

叶片进口安放角 28°

叶片数Z05

出口宽度 6.5mm

蜗壳 进口宽度 18mm

基圆直径 390mm

进口直径 58mm

导叶 进口角 12°

出口角 8.7/8.8/9.0°

弦长 143mm

高度 6.5mm

采用三维造型软件PROE对叶轮、 蜗壳及导叶等透平内部全流场计算区域进行三维建模，并对叶轮出口位置作适当延伸，即通过添加尾水管来保证流动的充分发展， 增强计算结果的稳定性。 以六叶片导叶透平为例，计算域模型如图1所示，选用3种不同黏度的纯液作能量回收工质，表1列出了其主要物性参数。

图1 计算域模型

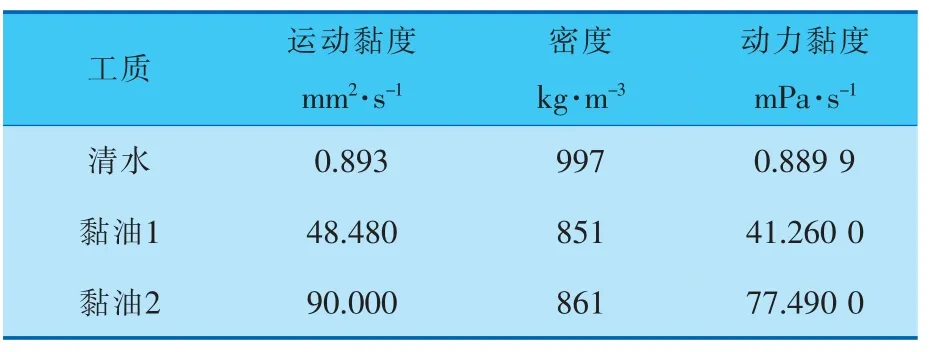
表1 工质物性参数（25℃，1atm）

2 数值计算

2.1 基本方程

对于旋转机械内部的流动， 可采用时均、不可压、粘性、定常流动的Navier-Stoke 方程来描述［15］。 连续性方程为：

式中 t——时间；

ui——速度矢量的i方向分量。

动量方程为：

式中 fi——i方向的体积力；

p——压强；

μ′——分子粘性系数；

μe——湍流粘性系数；

μt——涡粘性系数。

湍流动能和耗散率方程为：

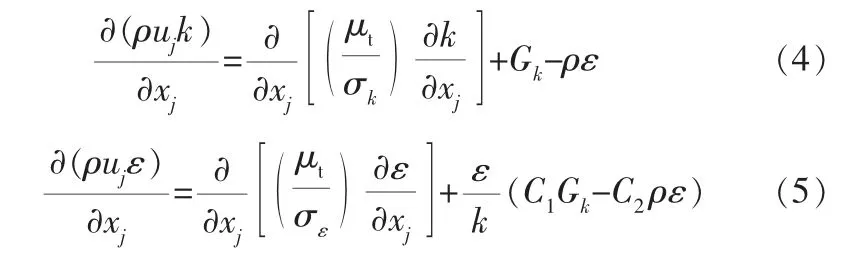
2.2 网格生成及数值模拟

以六叶片导叶透平为例，应用ICEM软件生成计算网格，采用对复杂几何边界适应性强的非结构化四面体网格对计算域进行网格划分。 无关性验证网格发现， 当整个计算域网格总数接近120万（ 其 中 蜗 壳494 088， 导 叶180 008， 叶 轮401 154，尾水管138 315）时，水力效率变化范围小于0.45%， 考虑到计算机的运算能力和计算精度，本次研究模型的网格数量均在120万左右。 应用计算流体动力学软件CFX对透平内部流动进行求解，动量方程和连续性方程采用SIMPLEC算法联立求解。 稳态计算边界条件为：边界设为质量流量进口，压力出口（0.5MPa），壁面条件为无滑移，近壁面采用标准壁面函数处理，计算收敛标准设为0.000 01。

3 计算结果与分析

3.1 性能曲线

从液力透平的外特性曲线（图2）可以看出，透平的水头随流量的增加而增加，相同流量下，导叶数越多，透平可回收的水头越大，且受工质粘性影响较小。 相同流量下 （清水工质72.8～93.6m3/h除外）， 透平的水力效率随导叶数的增加而升高，六导叶和八导叶透平在145.6m3/h下水力效率达到最高，十导叶透平在清水和黏油1工质时水力效率最高点对应的流量为135.2m3/h，黏油2工质时水力效率最高点对应的流量降至124.8m3/h。

图2 液力透平的外特性曲线

3.2 水力损失分布

水力损失指单位重量工质在液力透平各过流部分流动中损失的能量， 包括水力摩擦损失、冲击、脱流及速度改变等引起的损失。 具体数值可通过在CFD-POST提取相关参数并计算确定，即：

式中 Hth——透平理论水头，m；

Δhi——各过流部分内的水力损失，m；

Δhtotal——透平总水力损失，m。

表2列出了3种透平在不同黏度工质下最高水力效率点的水力损失，图3为3种透平在不同黏度工质下主要过流部分的水力损失分布状况。 对比图表可知，液力透平蜗壳内的水力损失在总损失中的占比约为6%～13%，叶轮内水力损失最大，在总水力损失所占比重超过50%， 导叶内的水力损失略大于蜗壳水力损失，尾水管内的水力损失略小于蜗壳水力损失；随工质黏度的增加，同种透平各过流部分内的水力损失基本上都有所增加；蜗壳内水力损失随流量的增大而增大，同种工质下3种透平蜗壳损失曲线接近重合， 表明导叶叶片数对蜗壳内水力损失影响很小；同种工质下导叶内的水力损失随流量的增大总体上呈增大趋势；清水工质相同工况下，导叶内水力损失随导叶数的增加而增大（六导叶72.8～93.6m3/h除外）， 这是由于导叶数增多导致其当量水力半径减小和叶栅中流速增加所致； 工质为黏油时，相同工况下六导叶内的水力损失最小（72.8～93.6m3/h除外），八导叶内的水力损失最大，且略大于十导叶内的水力损失；叶轮内水力损失随流量的增大先减小后趋于平缓，同种工质下叶轮内水力损失随导叶数的增加而减小；总水力损失随流量的增大先减小后增加， 最小总水力损失约在114.4m3/h附近，与最高效率点并不重合，这是因为透平水力效率是实际水头和总水力损失的二元函数；同种工质相同工况下，总水力损失总体上随导叶数的增加而减小。

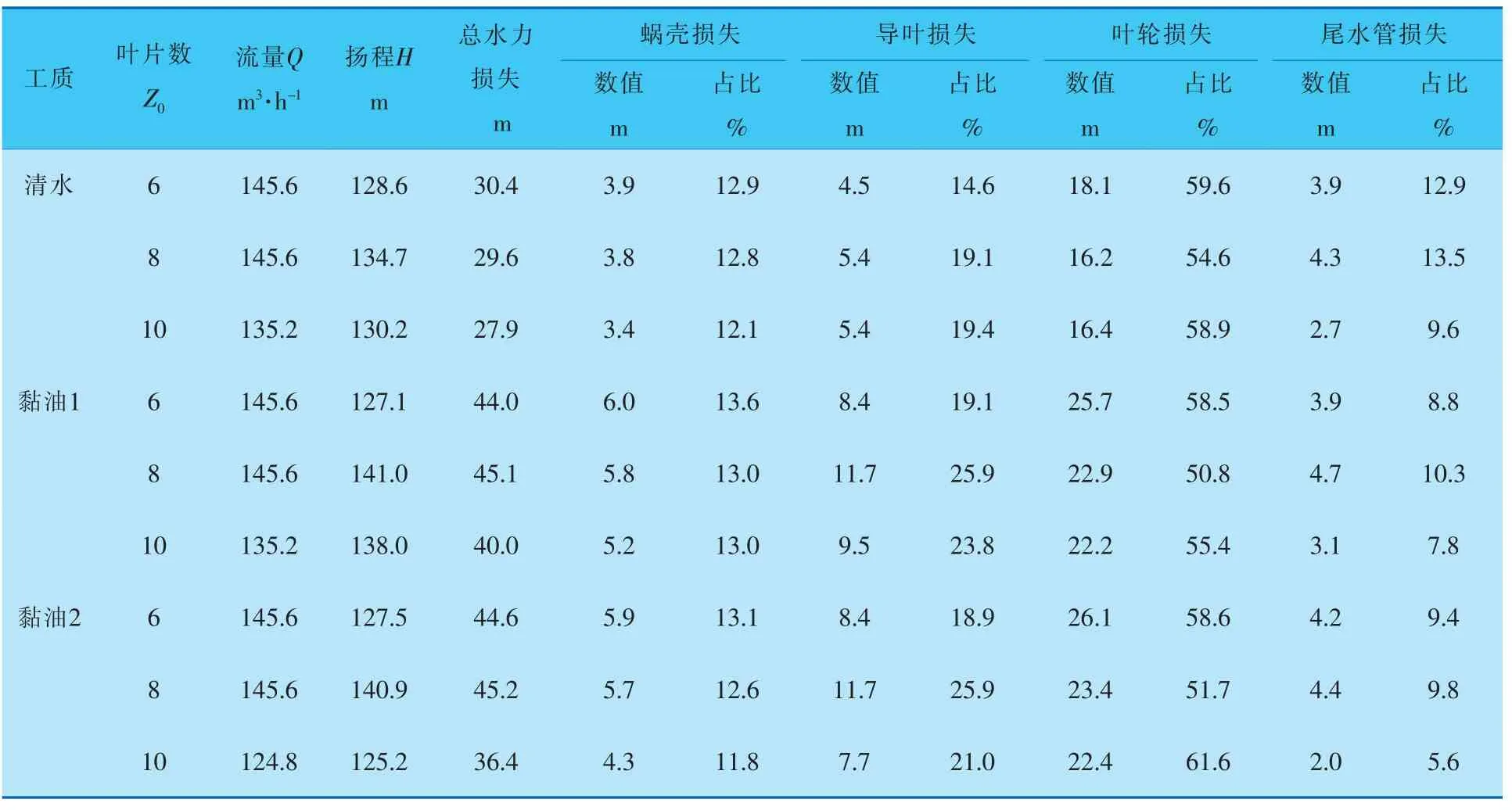
表2 3种透平在不同黏度工质下最高水力效率点的水力损失

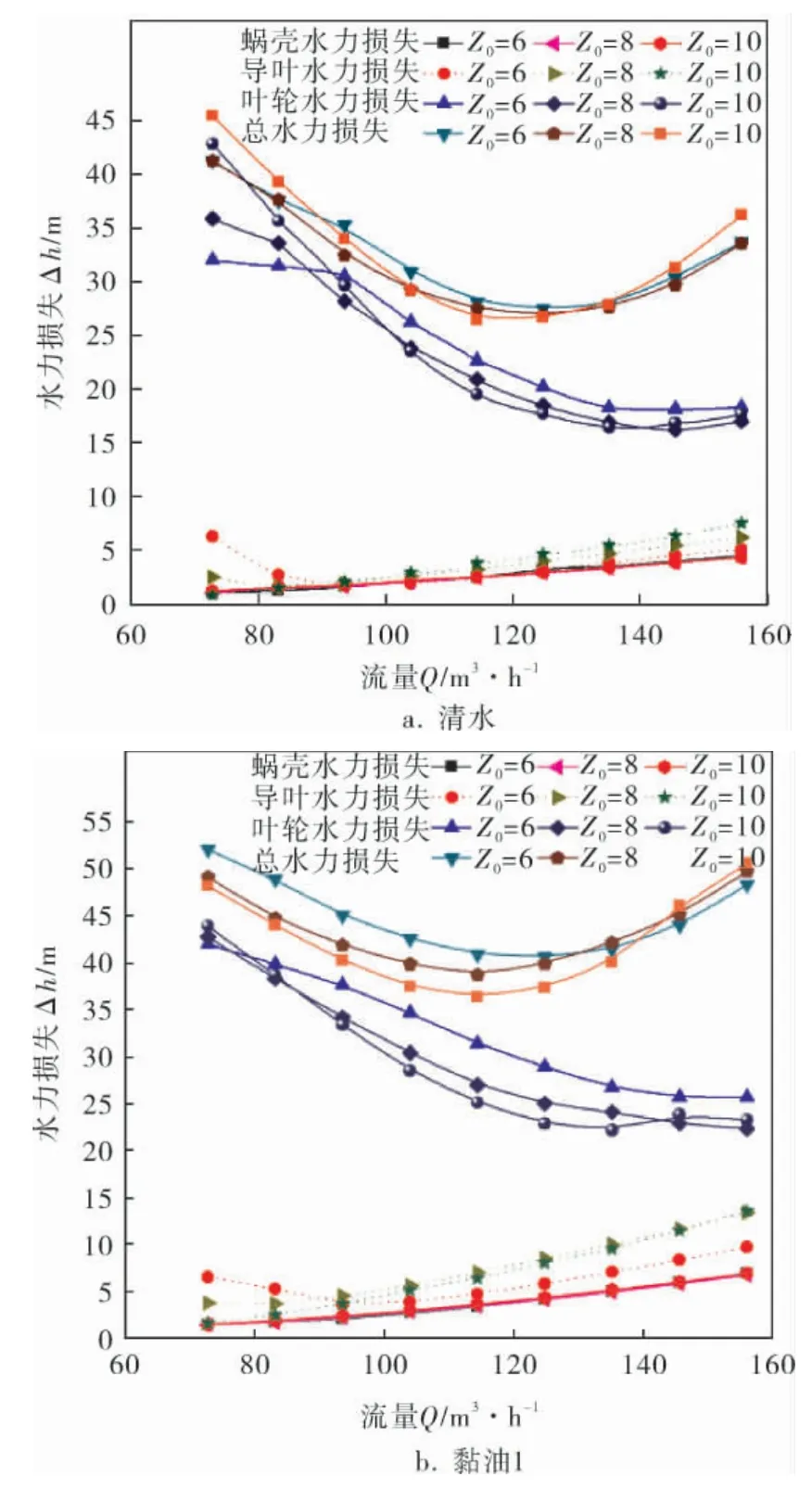
图3 3种透平在不同黏度工质下主要过流部分的水力损失分布

3.3 湍流动能耗散率

湍流动能耗散率与能量损失有关，是指分子在粘性作用下由湍流动能转化为分子热运动动能的速率， 图4为最优工况下不同工质时液力透平中间截面湍流动能耗散率分布云图。 可以看出，同种工质下，蜗壳内湍流动能耗散率值最低，分布最均匀；清水工质时，六导叶透平湍流动能耗散率的较高值集中分布在整个导叶流道和叶轮进口区域，随着导叶数的增多，湍流动能耗散率较高值集中分布的区域显著减小；随着工质黏度的增加，十导叶透平湍流动能耗散率较高值集中分布区域扩散相对最为缓和，结果表明合适叶片数的导叶可以改善透平内部湍流动能耗散率的分布状况。

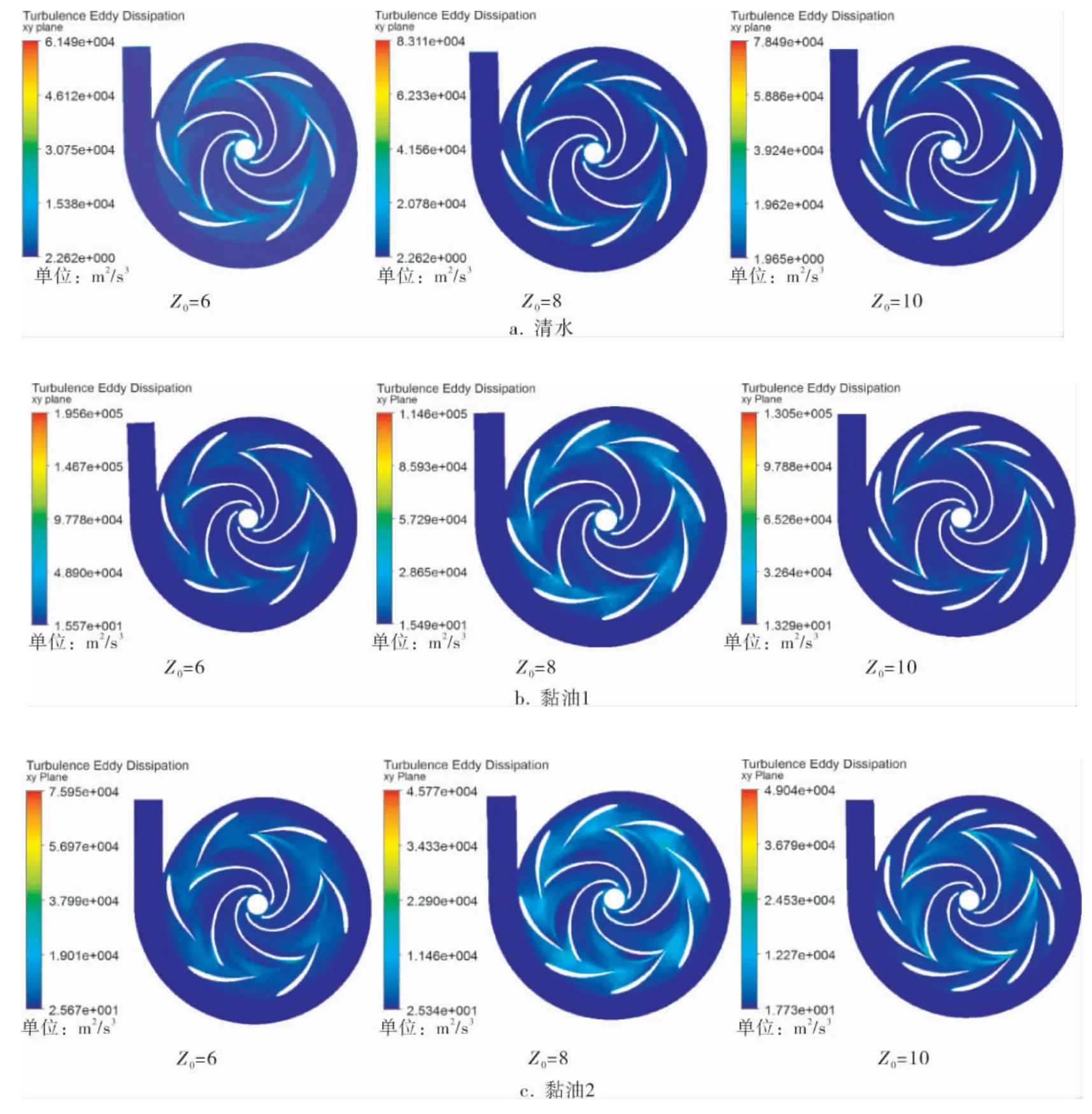
图4 最优工况下不同工质时液力透平中间截面湍流动能耗散率分布云图

图5为透平叶轮湍流动能耗散率体积加权平均值分布［16］。 可以看出，叶轮湍流动能耗散率随着导叶数的增加总体上呈减小趋势，受工质粘性影响较小；六导叶和八导叶叶轮内湍流动能耗散率呈类似正弦规律分布，十导叶透平叶轮内湍流动能耗散率呈类似余弦规律分布；不同黏度工质时各透平叶轮的湍流动能耗散率极小值均位于最优工况附近，而最优工况附近叶轮内水力损失也是最小值，表明此时透平叶轮内的水力损失主要以湍流动能耗散的形式转化为工质的热能。

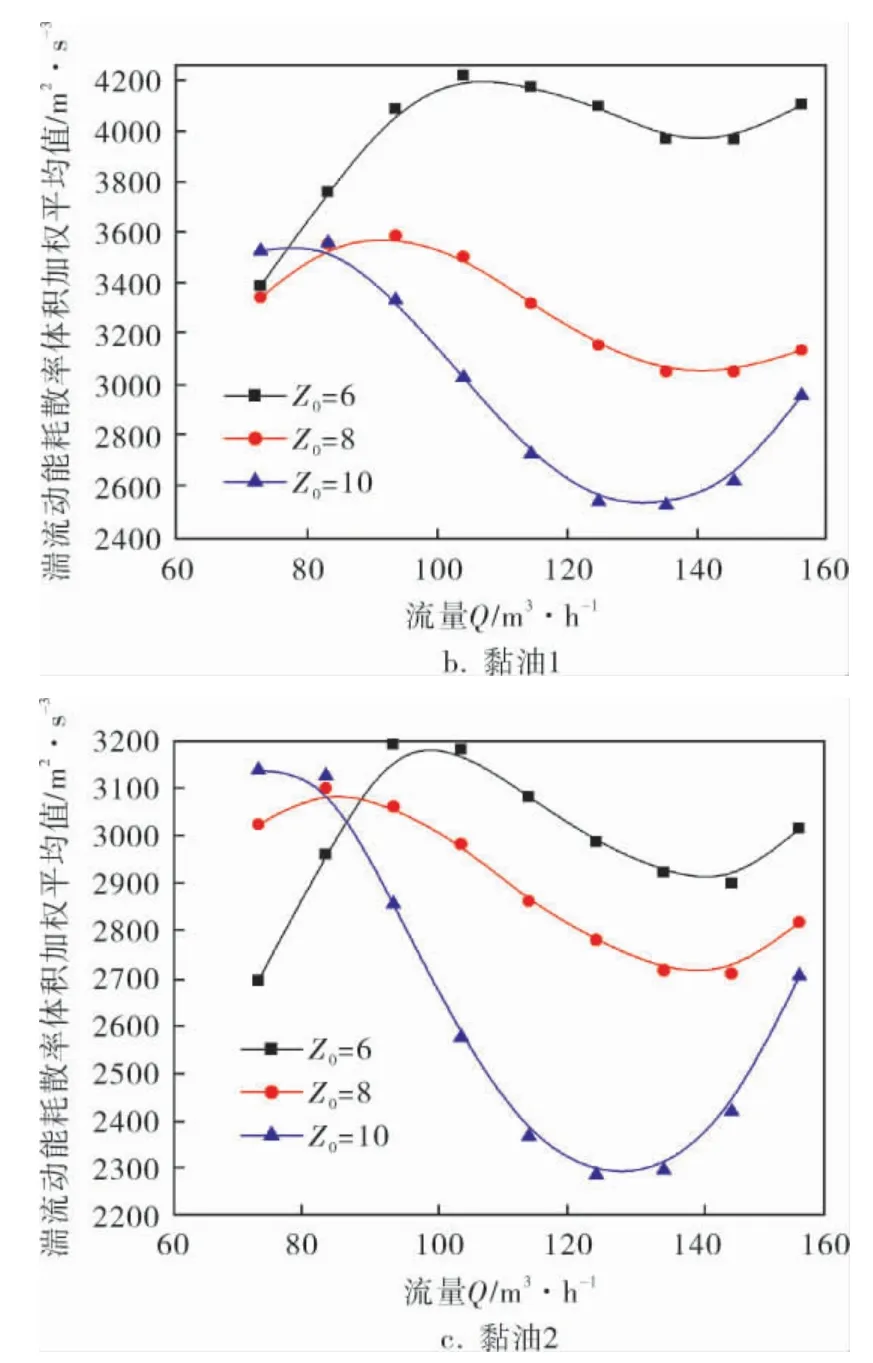
图5 透平叶轮湍流动能耗散率体积加权平均值分布

4 结论

4.1 不同工质下，叶轮内的水力损失在导叶式液力透平总水力损失中所占比重超过50%， 是水力损失的主要部分；相同工质下，叶轮内的水力损失随着导叶数的增加而减小， 叶轮内的流动受导叶数影响显著，蜗壳、导叶及尾水管等过流部分的流动受导叶数影响较小； 相同导叶数透平各过流部分的水力损失随工质黏度的增加呈增大趋势。

4.2 相同工质下，总水力损失随着导叶数的增加而减小；相同导叶数透平的总水力损失随着工质黏度的增加而增大；最优工况时，透平叶轮内的水力损失主要以湍动能耗散的形式转化为工质的热能。

4.3 最高效率点与叶轮最小水力损失工况基本一致，但与最小总水力损失工况无直接关系。