模糊微分方程可约的条件
吉利业,尤翠莲
(河北大学 数学与信息科学学院,河北 保定 071002)
模糊集理论[1]是由美国专家 Zadeh在1965年提出的,模糊数学由此产生.在经典集合理论的基础上,Zadeh提出了模糊集的概念.随后学者们通过建立隶属函数和相应的模糊集运算来分析模糊现象.为了衡量模糊事件的大小,Zadeh[2]又提出了可能性测度的概念.然而不足的是可能性测度不具有自对偶性.自对偶性是现实世界中十分必要的,为了解决这一问题,Liu等[3]提出了具有自对偶性的可信性测度.在2004年,Liu[4]建立了可信性理论并给出了可信性理论的4个公理.随后Li等[5]给出如何判断一个集函数是否为可信性测度的方法.2007年,Liu[6]将可信性理论进行了完善.从此,可信性理论得到稳步发展.
在可信性理论的框架下,Liu[6]提出了模糊变量的概念,即一种从可信性空间到实数集的函数.除此之外,模糊过程、模糊积分和模糊微分的概念也诞生了.为了解释模糊现象随时间的演变,Liu[6]提出模糊过程这一概念.最重要的模糊过程就是Liu过程[7],它和随机中的Brown运动具有同等地位.基于Liu过程,文献[7]提出了Liu 积分和Liu公式,它们类似于随机中的Ito积分和Ito公式.这些概念提出后,学者们做了大量工作.Qin等[8]把Liu过程从实数集推广到了复数集.2015年,You等[9]讨论了复Liu 积分的一些性质.You等[10]把Liu 积分和Liu 微分推广到多维情形.You等[11]给出广义Liu 积分的概念,并对一些性质进行了证明.目前学者们研究的模糊微分方程主要有2类:第1类是通过使经典微分方程的系数和初始条件模糊化得到的模糊微分方程[12-15].虽然方程的数值解法越来越吸引学者,但对其解析解的研究仍是相当重要的工作.近年来学者们利用各种工具或方法研究不同模糊微分方程的解析解,Hooshangian[16]和Altaie等[17]分别研究了模糊二阶微分方程和模糊偏微分方程的近似解析解.第2类模糊微分方程是由Liu过程驱动的微分方程.这类方程最早出现在文献[7]中,它的模糊性不仅体现在系数和初始条件上,还体现在驱动过程里.本文主要研究第2类模糊微分方程.
在模糊环境中,模糊微分方程是解决动态系统的有力工具,例如在科学、工程技术、金融投资等领域都会用到模糊微分方程去建立模型.You等[18]求出了线性模糊微分方程和部分非线性模糊微分方程的解析解,但仍有大量模糊微分方程不能得到解析解,所以You等[19]推导出模糊Taylor展开式,通过截断展开式得到一种Euler逼近法并且讨论了数值方法的收敛性.随后文献[20]中提出了一种基于模糊Taylor展开式来求模糊微分方程近似解的数值方法.在这2种模糊数值解法提出后,Cheng等[21]通过对Euler法进行改进提出新的数值格式.有关模糊微分方程数值解的研究将是未来模糊系统的一个重要研究方向.然而得到模糊微分方程解析解也是大家希望达到的目标.在求解析解的过程中,发现一类不能直接求出解析解、但能通过一个变量替换求解的非线性模糊微分方程,被称为可约模糊微分方程.因此,本文主要目的是找到辨别和求解可约模糊微分方程的具体方法.
1 预备知识
Liu过程是一种模糊过程,在模糊微分方程的理论及应用中得到了广泛的应用.
定义1[7]一个模糊过程如果满足如下3个条件就称为Liu过程.
1)C0=0;
2)Ct具有独立且稳态的增量;
3)对于每一个固定时刻t,Cs+t-Cs是一个正态模糊变量,期望为et,方差为σ2t2.
如果e=0且σ=1,那么Ct是一个标准的Liu过程.
定理1[7](Liu公式)假设Ct是一个标准的Liu过程,h(t,c)有连续的偏导数.令Xt=h(t,Ct),则

此时称Xt关于CtLiu可积.
定义3[7](由Liu过程驱动的模糊微分方程)如果Ct是一个标准的Liu过程,并且f和g是给定的函数,Xt是未知的模糊过程,则方程
dXt=f(t,Xt)dt+g(t,Xt)dCt
称为由Liu过程驱动的模糊微分方程.
在文献[18]中,模糊微分方程分为线性模糊微分方程,广义线性模糊微分方程,齐次模糊微分方程和可约模糊微分方程.
形如
dXt=(a+bXt)dt+(c+dXt)dCt
的方程叫做线性模糊微分方程,其中a、b、c和d是常数.当a=c=0时,方程被称为线性齐次模糊微分方程.
形如
dXt=(u1t+u2tXt)dt+(v1t+v2tXt)dCt
的方程叫做广义线性模糊微分方程,这里的u1t、u2t、v1t和v2t是给定的模糊过程,并且与Xt、Ct无关.这个方程的解为
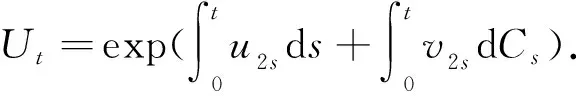
本文将线性和广义线性模糊微分方程统称为线性模糊微分方程.其他模糊微分方程统称为非线性模糊微分方程.
形如
dXt=f(Xt)dt+g(Xt)dCt
的方程叫做齐次模糊微分方程,此处f和g都是给定的函数.
一个非线性模糊微分方程如果可以通过变量替换转化为线性模糊微分方程,进而求解,称这样的方程为可约模糊微分方程.
2 可约模糊微分方程
应用一个恰当的替换Yt=U(t,Xt),非线性模糊微分方程
dXt=f(t,Xt)dt+g(t,Xt)dCt
(1)
可以转化成一个关于Yt的线性模糊微分方程
dYt=(γtYt+αt)dt+(δtYt+βt)dCt.
(2)

结合方程(2),可得
(3)
(4)
借此推导出非线性模糊微分方程转化成线性模糊微分方程的条件,得到以下定理.
定理2令
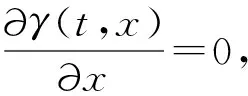
αt和βt是模糊过程,C是任意常数.
证明:对方程(1)作变量替换Yt=U(t,Xt)后,令γt≡δt≡0,根据式(3)可得
对上式两边关于x求导,则
(5)
由式(4),可得
上式两边对t求导,
(6)
将式(5)代入式(6),如果g(t,x)≠0,那么


定理得证.
注1:此定理并不表示非线性模糊微分方程通过变量替换求解时替换形式唯一.
例1求解非线性模糊微分方程
(7)

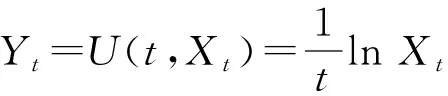
定理3若函数a(x)和b(x)是二次可微函数,则模糊微分方程dXt=a(Xt)dt+b(Xt)dCt可以通过替换Yt=U(Xt)转化成线性模糊微分方程dYt=(a1Yt+a2)dt+(b1Yt+b2)dCt,其中
其中
b2可以任意选择,C1、C2是任意的常数.
证明:根据式(1)-式(4),如果齐次模糊微分方程
dXt=a(Xt)dt+b(Xt)dCt,
可以通过替换Yt=U(Xt)转化成
dYt=(a1Yt+a2)dt+(b1Yt+b2)dCt,
那么
(8)
(9)
接下来分2种情况寻求U(x)的表达式.
第1种情况,假设b(x)≠0且b1≠0,由式(9)可得
(10)

即
(11)
对式(11)求导,有
(a′(x)b(x)-b′(x)a(x))(b′(x)-b1)+a(x)b(x)b″(x)-a″(x)b2(x)=0.
所以
从而得到U(x).
另一种情况,如果b1=0,根据式(9)可得
U(x)=b2B(x)+C2,
(12)
b2可以在满足式(8)的情况下任意选择,C2是任意常数.
定理得证.
下面通过2个算例来验证定理3的有效性.
例2设Ct是一个标准的Liu过程,a、b、k是正数,考虑模糊微分方程
dXt=k(a-lnXt)Xtdt+bXtdCt
(13)
的解.

则原方程的解为
例3令Ct是一个标准的Liu过程,假设a、b、k是正数,考虑模糊微分方程
(14)
的解.

所以模糊微分方程(14)的解为
从目前研究看来,很多非线性齐次模糊微分方程都是可约的,可以转化为线性模糊微分方程,但是也有一部分是无法确定的,仍需进一步研究.
3 结论
本文讨论了非线性模糊微分方程的可约条件和求解方法,其中包括如何判别一般非线性模糊微分方程是否可约以及如何转化为线性模糊微分方程的方法,还包括非线性齐次模糊微分方程的可约方法.即使需要大量的运算,但仍有助于更简便地求解非线性模糊微分方程.尽管如此,由于并不是所有非线性模糊微分方程都是可约的,故关于非线性模糊微分方程的求解仍需进行研究.

