某型地铁车辆设备吊挂刚度与车体模态匹配研究*

王思明， 张立民

(西南交通大学 牵引动力国家重点实验室， 成都 610031)

轨道交通中，车体弹性对车辆运行的平稳性影响很大，因此考虑车体弹性振动对人体乘坐舒适度影响越来越受到重视[1-2]。弹性车体平稳性变差的主要原因为车体的垂向一阶弹性振动[3]。同时，车辆下部设备的吊挂方式对弹性车体的整车振动模态有很大影响，车下设备的弹性吊挂相比刚性吊挂能够降低车体的垂向振动水平与提高(一阶)垂向弯曲频率[4-5]。因此车下设备浮沉频率与车体一阶垂弯振动频率匹配非常重要。一般情况下为了避免共振的发生，根据振动理论车下设备浮沉频率设置要避开车体一阶弯曲频率[6]。但是文献[7]研究指出车下设备的浮沉频率接近车体垂向弯曲频率时，车体的振动响应才会最小，此时车下设备起到动力吸振器作用。因此采用设备浮沉频率避开车体一阶弯曲频率的设计原则不一定是最佳选择。

基于此，文中在地铁车辆空气弹簧位置和车下设备分别激励情况下，计算车下设备吊挂刚度值对车体振动响应的影响。通过对比分析，得出在车体一阶垂弯模态频率与吊挂设备浮沉频率最佳匹配，为车下设备吊挂刚度设计提供参考。

1 车体有限元模型

以某型地铁车辆整备车体(有附属设备和内饰，无窗、门和座椅)为计算对象，其车体为钢铝复合结构，整备状态总重为20.549 t。车体主要附属设备有车顶空调、牵引逆变器和辅助变流器等。2台车顶空调以刚性固定方式安装，每台质量650 kg。牵引逆变器和辅助变流器质量分别为1 350 kg和680 kg，以某一刚度的弹性吊挂方式安装在车体中部车下横梁上。其他质量较轻的车下设备如风缸、控制箱等，则以刚性固定方式安装在车下横梁上。

根据车体的三维模型建立有限元模型如图1所示，为了得到尽可能详细的车体局部振动响应，车体划分为1 658 911个单元，结构阻尼比设置为0.01。

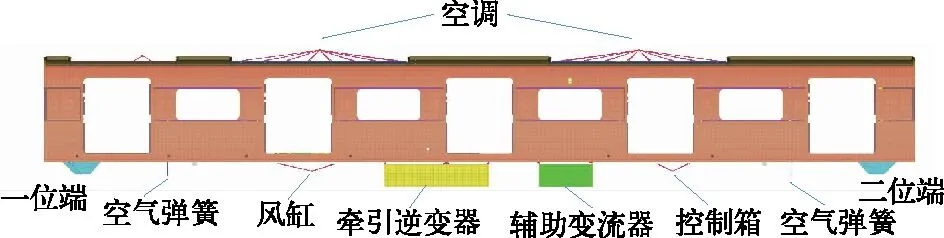
图1 车体有限元模型

2 吊挂刚度对车体模态的影响

车下设备中牵引逆变器和辅助变流器质量较大，其上均安装有冷却风机，且有高频磁致振动，为有源振动设备(以下对牵引逆变器和辅助变流器简称为有源设备)，因此主要考虑这2种设备的吊挂刚度对车体模态振动影响。在有源设备的吊挂分别为刚性和弹性2种情况下对车体有限元模型进行模态计算。吊挂为弹性时只考虑有源设备垂向固有频率为10 Hz时的情况，弹性吊挂阻尼比设置为0.1。在此2种情况下计算得出车体一阶振动各模态频率如1表所示。

表1 车体振动模态频率 Hz

由表1可知，车体菱形、垂弯、扭转、呼吸和横弯的一阶模态频率分别由刚性吊挂时的7.08 Hz、8.30 Hz、9.75 Hz、13.75 Hz和14.47 Hz变为弹性吊挂时的6.78 Hz、10.16 Hz、9.76 Hz、13.90 Hz和15.84 Hz，这说明弹性吊挂可使车体一阶的垂弯、扭转、呼吸和横弯振动模态频率增加，但使一阶菱形模态频率有所降低。其中，吊挂刚度变化对车体一阶垂弯振动模态影响最大。

3 刚度匹配计算

以上计算表明，车下设备的吊挂刚度与车体振动模态频率关系密切。因此，对车体在空气弹簧位置和有源设备上先后分别加正弦扫频激励，模拟车辆运行中车体受到不同频率的激励。通过改变车下有源设备吊挂的刚度值，分析扫频激励过程中车体地板位移振动响应，得到吊挂刚度与车体一阶垂弯振动模态最佳匹配值。

因车体振动模态中一阶垂弯振动对平稳性影响最大[1]，所以吊挂刚度取值分布通过车体一阶垂弯模态频率与有源设备垂向固有频率的比值λ来确定，即

(1)

式中：fc为车体一阶垂弯模态频率；fe为有源设备的垂向固有振动频率。

由上节车体模态计算结果可知，在车下有源设备为刚性吊挂时，车体一阶垂弯模态频率为8.30 Hz；而在弹性吊挂时，车体一阶垂弯模态频率为10.16 Hz。为方便计算，式(1)中车体频率一阶垂弯模态频率fc取为9 Hz，则频率比λ分别为0、0.3、0.7、1.0和1.4时，由式(1)得到吊挂设备垂向振动频率和吊挂刚度值如表2所示，每个吊挂的垂向阻尼比均设置为0.1。

表2 设备弹性吊挂刚度值分布

扫频激励分空气弹簧位置和有源设备激励2种情况，均采用垂向同步加载方式，即各加载位置的激励载荷相位相同。激励频率范围取为5～100 Hz，步长0.25 Hz，幅值为1 kN。由于车体为对称结构，因此只在车体一位端端部、一位端空气弹簧上方和中部地板上取测点，观测其振动位移的频率响应情况。

4 计算结果及分析

4.1 空气弹簧位置激励

空气弹簧位置激励情况下，车体地板各测点在不同频率比λ时的振动位移幅频响应曲线如图2～图4所示。

图2 一位端端部地板位移幅频响应

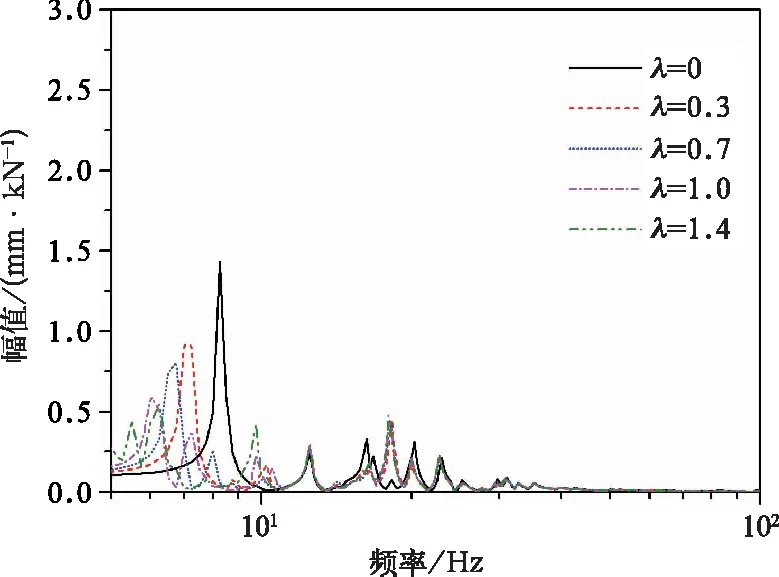
图3 一位端空气弹簧上方地板位移幅频响应

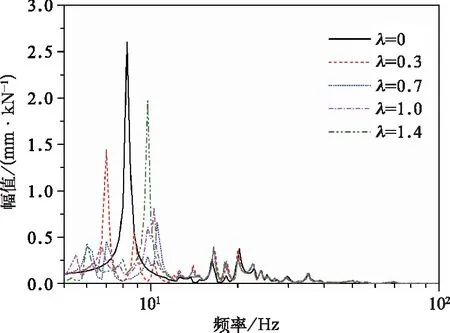
图4 车体中部地板位移幅频响应

由图2～图4所示曲线可看出，在频率9 Hz附近，空气弹簧上方地板振动幅值最小，这是因为车体一阶垂弯振动模态的节点在空簧位置附近。设备吊挂在不同刚度值时，地板各测点的幅频响应均以频率12 Hz和40 Hz为分界点分为3种不同振动类型的振动频段。第1频段在12 Hz以下，地板振动响应受吊挂刚度的影响较大，振动幅值迥异，由第3节可知，该幅值为车体一阶垂弯振动引起。第2频段为12 Hz至40 Hz频率范围内，地板在不同吊挂刚度下的振幅趋于一致，说明该频段地板振动响应主要取决于车体的自身特性。第3频段为40 Hz以上，此时地板的振动位移幅值很小。从响应曲线的第2频段和第3频段可以看出，在12 Hz以上激励时，吊挂刚度变化地板幅频响应基本没有影响。

从图4中可以看出，相比λ=0时，在λ=0.3时车体中部地板最大振幅由2.6 mm/kN降低为1.5 mm/kN，而峰值频率却由8.25 Hz减少到了7.00 Hz。这是由于车下设备在横梁上的刚性固定，有助于增加车体整体刚度，从而增加车体一阶垂弯模态频率。但在λ=0.7、λ=1.0和λ=1.4时，峰值频率则增加到10 Hz以上，说明此时弹性吊挂的刚度对地板振动的影响增大。

根据动力减振器的理论，在频率比λ=1.0时车体的一阶垂弯模态振动幅值应当最小，但通过图4可知，在9 Hz附近，地板上各测点振幅均值在频率比λ=0.7时最小，此为吊挂刚度与车体一阶垂弯振动模态最优匹配值。这是因为车下设备是固定在车下横梁上的，横梁有一定的弹性，与车下吊挂串联后降低了车下设备振动频率，并使车下设备实际振动频率在λ=0.7时比λ=1.0时更接近接近车体一阶垂弯模态频率。

通过以上分析可知，该地铁车辆运行时，车体地板的振动响应频率主要集中在40 Hz以下；其中，地板振动响应在12 Hz以下的低频段取决于车体振动模态和车下设备吊挂刚度值匹配情况，在12 Hz以上时主要取决于车体振动模态；车下设备的吊挂刚度取值使其浮沉频率略大于车体一阶垂弯模态频率，可使车体振动响应幅值最小。

4.2 有源设备激励

有源设备激励时，车体地板各测点在不同频率比λ时的振动位移幅频响应曲线如图4～图6所示。

由图5～图7中所示曲线可以看出，设备激励时地板各测点的位移幅频响应相似，振动响应主要集中在20 Hz以下，这说明有源设备激励引起地板的振动响应还取决于车体自身的振动特性。同时可知，如果车下有源设备工作时振动频率在20 Hz以上，取不同吊挂刚度在地板上引起的振动响应幅值均很小，此时设计设备吊挂刚度，可以不考虑吊挂刚度对车体振动的影响。

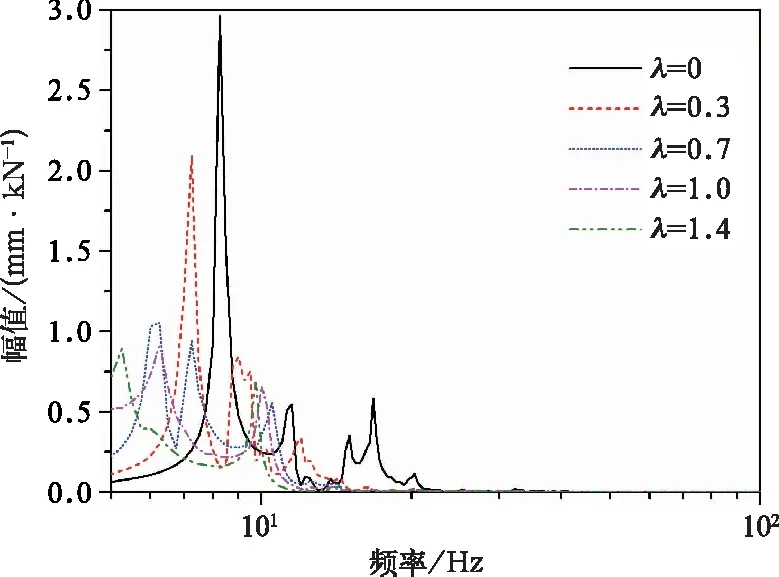
图5 一位端端部地板位移幅频响应

图6 一位端空气弹簧上方地板位移幅频响应

图7 车体中部地板位移幅频响应

设备激励时，吊挂刚度与车体振动模态的匹配依然对车体一阶垂弯振动响应有很大影响。设备激振频率在车体一阶垂弯频率附近时，相比频率比λ=0，吊挂刚度在频率比λ=0.3时地板振幅改善不大。但在频率比λ=0.7、λ=1.0和λ=1.4时，地板振幅减小较多，尤其在地板端部和中部。但在频率比λ=0.7、λ=1.0和λ=1.4之间相比，地板振幅响应大小基本相似。可见，设备激励时，吊挂刚度值要取到频率比λ=0.7以上才能较好的改善车体的振动响应。

通过以上分析可知，该地铁车辆有源设备工作频率在20 Hz以上时，对车体地板振动的影响很小；设备的激励频率在车体一阶垂弯频率附近时，弹性吊挂的刚度小于一定值时才能有效地减小地板振动的响应幅值。

5 结 论

通过对某型地铁车辆车体有限元模型计算分析可知，车下设备的吊挂刚度对车体振动模态频率有不同程度的影响。空气弹簧位置和车下设备分别激励时，车体地板振动响应均是由车下设备吊挂刚度和车体振动特性共同决定的，响应频率集中在一定频率以下；合适的吊挂刚度值可有效地改善车体地板的振动状态。