利用一致性分析的高维类别不平衡数据特征选择
曾海亮,林耀进,王晨曦,陈祥焰
(闽南师范大学 计算机学院,福建 漳州 363000) (数据科学与智能应用福建省高等学校重点实验室,福建 漳州 363000)
E-mail:zzlinyaojin@163.com
1 引 言
在文本分类[1]、图像识别[2]、医学诊断[3]等研究领域,数据呈现出高维小样本特点,即特征空间显示高维性,而样本数量过少.此外,该类数据通常伴随着类别不平衡问题,如某一类的样本数量远大于另一类的样本数量,易引发分类学习过程中大类样本覆盖小类样本现象,而实际中小类样本往往是关键的样本[4].例如,信用记录欺诈用户的数量明显低于正常用户;常规体检中重疾患者占极小比例.因此,如何提高高维类别不平衡数据中小类样本的分类学习精度具有重要意义.
众所周知,在高维类别不平衡数据分类建模任务中存在着小类样本难以正确分类问题.为了提高小类样本的预测精度,研究人员提出了众多的类不平衡特征选择算法[5-8].文献[5]通过组合预先分别选择的正特征和负特征,以期改善文本分类中类不平衡数据的分类性能.文献[6]使用五种微阵列表达数据集对九种过滤技术进行了系统比较与分析,研究了抽样技术在特征选择中的应用,发现特征选择有利于处理类不平衡数据.文献[7]通过重构邻域粗糙集下近似算子,提出了基于特征和标记之间依赖关系的在线特征选择框架,旨在处理流特征环境下的类不平衡问题.文献[8]运用了基于小类依赖度的在线流式特征选择模型,并改进了邻域粗糙集的依赖度计算公式.
在高维类别不平衡数据多分类学习任务中,若数据中类别分布倾斜得十分明显时,特征选择技术可以将所有样本都分到大类从而获得很高的分类精度.然而,却忽略了至关重要的小类样本,失去了实际意义.另外,有些特征选择方法[9]将数据集某一类设置成小类样本,其余类别样本设置成大类样本,这种人为设置大小类具有一定主观性,很难体现数据的多样性与复杂性.
从认知角度出发,样本在论域空间的分布随特征的变化而变化,具有高可分离性的特征应使样本类内分散度尽量小,类间分散度尽量大.基于此,选择好的特征能显著提高高维类别不平衡数据的分类性能.基于最近邻思想,相同特征空间下越相近的样本其类别往往比较一致.于是,本文通过定义样本一致性概念来构建高维类别不平衡数据特征选择模型.首先,通过样本在特征与类别标记的信息定义样本的近邻,并设计面向高维类别不平衡数据的一致性分析模型;其次,根据特征重要度公式构造前向贪婪搜索算法进行特征选择;最后,通过实验表明该模型的有效性.
综上,本文内容安排如下:第二节设计利用一致性分析的高维类别不平衡数据特征选择的模型与算法;第三节对所提算法进行实验验证与结果分析;第四节总结全文.
2 利用一致性分析的高维类别不平衡数据特征选择
在实际应用场景中,数据的样本类别呈现多类及类别比例差异大等特点,而且小类样本在众多样本中占据着举足轻重的地位.为此,本文通过定义样本的一致性来进行高维类别不平衡数据的特征选择.首先,基于特征空间的样本距离来定义目标样本的近邻,并根据目标样本所在类别的数量来定义近邻的大小;其次,定义目标样本近邻空间内类别一致的近邻与论域中所有同类样本的比例称为包含度,包含度反应特征对样本的区分与类别空间对样本区分的一致性,而且能有效地避免小类样本被大类样本覆盖的情况.基于该一致性,可以定义特征对类别标记的重要度,并设计相关的前向贪婪搜索算法.

表1 高维类别不平衡数据示例表Table 1 Example of high-dimensional class-imbalanced data
定义1.给定论域空间内决策系统
κS(xi)={x|x∈Minnj{ΔS(x,xi)},x∈U}
(1)
其中,ΔS(x,xi)表示样本xi与任意样本的距离,Minnj{ΔS(x,xi)}表示与样本xi距离最近的前nj个样本的集合,如图1所示.
例1.由表1所示,给定特征f1,样本x1,因x1∈X1,有n1=|X1|=3,则Min3{Δf1(x,x1)}={x1,x3,x5},所以目标样本x1的近邻空间为κf1(x1)={x1,x3,x5}.
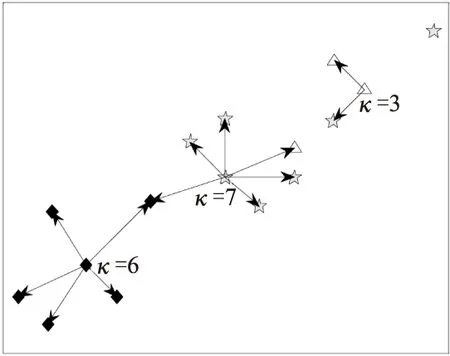
图1 实数空间中样本的近邻关系Fig.1 Near neighbor relationship of sample in real spaces
定义2.给定论域空间内决策系统
(2)
其中,κS(xi)表示样本xi在特征子集S条件下的近邻,Xj表示第j类样本的集合,I(κS(xi),Xj)表示样本xi的包含度.表明样本xi由特征子集S诱导出的近邻空间与类别诱导出的类别空间的包含程度.
例2.由表1所示,给定特征f1,样本x1,因x1∈X1,有n1=|X1|=3,则x1的近邻空间κf1(x1)={x1,x3,x5},而κf1(x1)∩X1={x1,x3},故I(κf1(x1),X1)=2/3.
定义3.给定论域空间内的决策系统
(3)

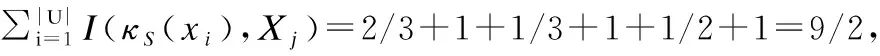
定义4.给定论域空间内的决策系统
sig(f,S,L)=CONS∪f(L)-CONS(L)
(4)
标记对特征的包含度函数定义了特征对分类的贡献,因此,可以作为特征集合重要性的评价指标.
根据定义4的特征重要度函数利用前向贪婪搜索算法依次对特征空间迭代直至终止条件得到的特征选择结果即为最终选择的特征.因此,本文将基于一致性函数,构造一种前向贪婪搜索特征选择算法.该算法以空集为起点,每次计算全部剩余特征的特征重要度,从中选择特征重要度值最大的特征加入特征选择集合中,直到所有剩余特征的重要度为0,即加入任何新的特征,系统的一致性函数值不再发生变化为止.
根据以上分析,利用一致性分析的高维类别不平衡数据特征选择算法具体描述如算法1所示.
算法1.利用一致性分析的高维类别不平衡数据特征选择(Feature Selection of High-dimensional class-imbalanced data using Consistency analysis,简称FSHC)
输入:
输出:约简后red
1. Ø→red
2. ∀f∈F-red/*计算样本距离关系矩阵Nred和Nred∪f,若Nred=Ø,则不计算*/
3. fori=1,2,…,ndo/*n为总样本数,即|U|=n*/
4.xi∈Xj,nj=|Xj|
5.κ(xi)=(x|x∈Minnj{Δ(x,xi)},x∈U}
6.I(κ(xi),Xj)=|κ(xi)∩Xj|/|κ(xi)|
7. end for
9. 计算sig(f,red,L)=CONred∪f(L)-CONred(L)
10. 选择f′满足sig(f′,red,L)=maxsig(f,red,L)
11. ifsig(f′,red,L)> 0 then
12.red∪f′→red
13. go to step 2
14. else
15. returnred
16. end if
算法1中第3-8步计算特征与标记的一致性值,第9-12步利用前向贪婪搜索策略对特征进行选择.假设论域空间有n个样本,f个特征,则该算法的时间复杂度为O(n·f2).
3 实验结果与分析
3.1 实验数据
为了验证FSHC算法的有效性,选取12个高维数据集进行实验,包括9个类别不平衡数据集和3个常规数据集,其中,brain、car、dlbcl、DrivFace、glioma、lung、lung2、lymphoma、srbct为类别不平衡数据集,colon、mll、prostate为常规数据集,描述信息见表2.对多类别数据集而言,由于类别存在对立的关系,当类别足够多样时,遍历到某一类样本即可视为小类样本,假设为正类,其余类样本即为异类,同理,遍历其余类别样本亦如此.

表2 类别不平衡数据集和常规数据集Table 2 Class-imbalanced data sets and routine data sets
为了更直观地呈现数据集的相关信息,采用相关矩阵图可视化高维数据的标记信息,矩阵图用灰度刻画类别及样本数量,右边细纵轴刻度代表类别,一种灰度表示一个类别,类别自下而上有序排列,左边纵轴刻度代表样本数量,样本数自下而上递增,一个色块表示该类别拥有的样本数量,详见图2.
3.2 评价指标
在高维小样本数据的分类学习过程中,对分类精度而言,即使类别不平衡问题造成小类样本的误判,无法区分小类样本的算法依然可以有比较高的精度,因此,本文实验结果的评价指标采用F-Score、G-Mean、分类精度,其中,F-Score和G-Mean是两个评价算法对于类别不平衡数据集小类样本分类性能的重要指标.关于F-Score和G-Mean评价指标的正负例样本的划分,本文算法采用依次遍历数据的样本类别.假设当前遍历到的类别为正类,则其余类别为异类,属于正类的样本为正例样本,属于异类的样本为负例样本.然后分别求各类别的F-Score值和G-Mean值,再求均值作为最终的F-Score值和G-Mean值.
设TP为真正例,TN为真负例,FP为假正例,FN为假负例,则查准率为P=TP/(TP+FP),查全率为R=TP/(TP+FN),F-Score定义为:
(5)
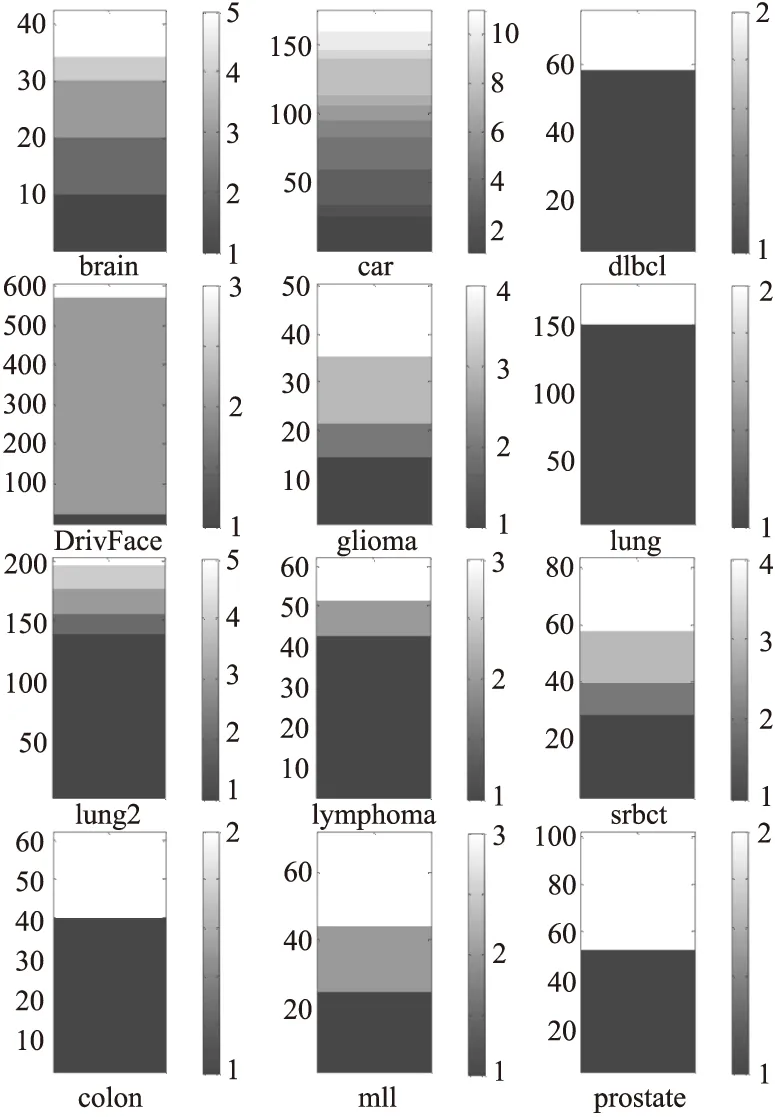
图2 高维数据集的相关矩阵图Fig.2 Correlation matrix of high-dimensional data sets
G-Mean定义为:
(6)
为了显示算法的统计显著性,使用基于算法排序的Friedman检验,假定在N个数据集上比较k个算法,令ri表示第i个算法的平均序值,定义Friedman统计量为:
(7)
其中,
(8)
若“所有算法的性能相同”的假设被拒绝,则表明算法的性能显著不同,此时以Nemenyi后续检验进一步区分,Nemenyi检验计算出平均序值差别的临界值域为:
(9)
3.3 实验设置
本文实验全部运行在3.10GHz处理器,4.00GB内存,windows 7系统及Matlab 2013的实验平台上.为减少因各特征量纲不一致对实验结果造成影响,采用离差标准化将所有数据的属性值归一化到[0,1]区间.
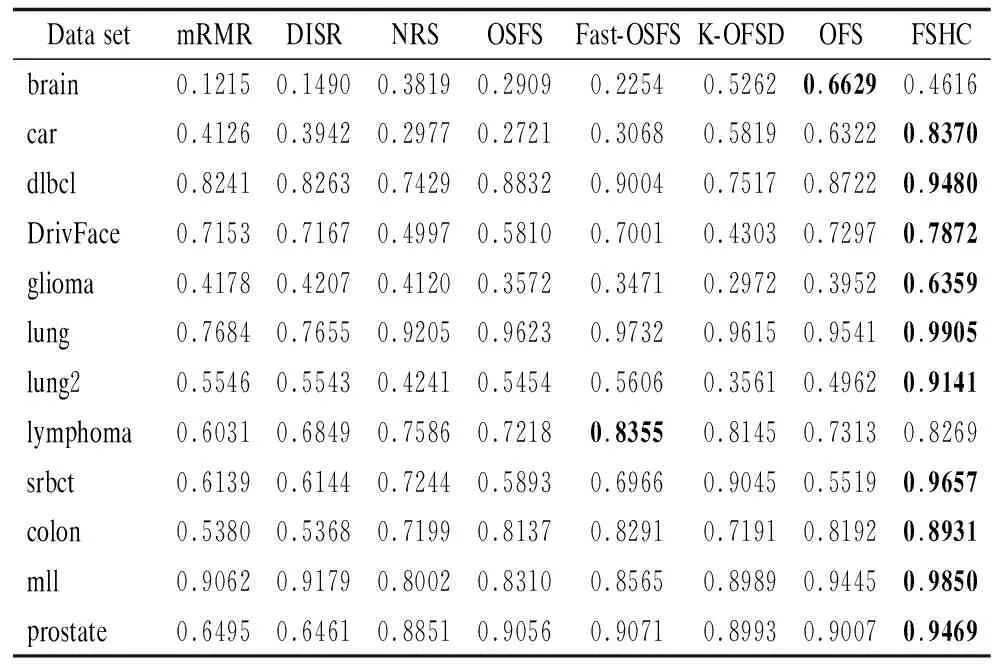
表3 平均F-Score值Table 3 Average F-Score value
为了检验算法的有效性,实验采用mRMR[10]、DISR[11]、NRS[12]等经典特征选择算法,以及OSFS[13]、Fast-OSFS[13]、K-OFSD[7]、OFS[8]等在线特征选择算法作为对比算法.基分类器为RBF-SVM,且采用5折交叉验证.由于mRMR、DISR算法的特征选择结果为特征排序,NRS、OSFS、Fast-OSFS、OFS、K-OFSD、FSHC算法的特征选择结果为特征子集.为了公平比较,排序法算法mRMR、DISR特征排序中的特征数量设置为子集法算法NRS、OSFS、Fast-OSFS、OFS、K-OFSD、FSHC特征选择结果中特征数最多的数目,并从第一个开始取.NRS的邻域参数δ设置为0.1.OSFS和Fast-OSFS采用Fisher′s Z test方法度量特征的相关性,显著性水平的参数α设置为0.01[14].K-OFSD和OFS中的近邻参数k取7,特征与标记的相关性阈值β设置为0.5,OFS中参数n取4,以类别包含数量最少的样本为小类样本[7,8].
3.4 实验分析
3.4.1 预测精度分析
实验数据表3-表5分别给出了各算法在各数据集上特征选择子集的平均F-Score值、平均G-Mean值以及平均分类精度和标准差.其中,标注黑体部分代表该算法在此数据集上的性能最优.
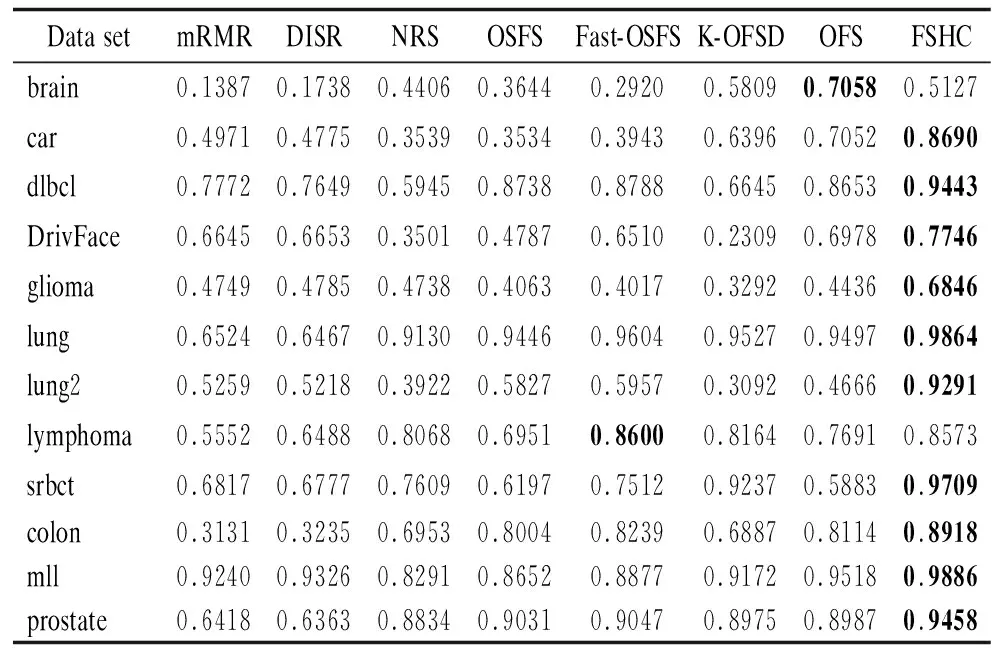
表4 平均G-Mean值Table 4 Average G-Mean value
由表3和表4可见,在类不平衡数据集brain上算法FSHC的分类性能逊于K-OFSD、OFS,在类不平衡数据集lymphoma上算法FSHC的分类性能逊于Fast-OSFS. 除以上两个数据集外,算法FSHC的分类性能均优于对比算法.表5给出了特征选择子集的平均分类精度和标准差,分类精度越高说明样本分类越准确,标准差越小说明分类稳定性越高.不难看出,在平均分类精度方面,除了在类别不平衡数据集brain上算法FSHC的分类精度略逊于算法K-OFSD、OFS外,FSHC的分类精度均优于对比算法.
F-Score和G-Mean是两个评价算法对小类样本分类性能的重要指标,FSHC算法在这两个评价指标上都获得了很高的值,由此可见,利用一致性分析的高维类别不平衡数据特征选择算法,相对于经典特征选择算法或者在线流特征选择算法在处理高维小样本数据分类学习任务中的类不平衡问题方面具有更高效的表现能力.
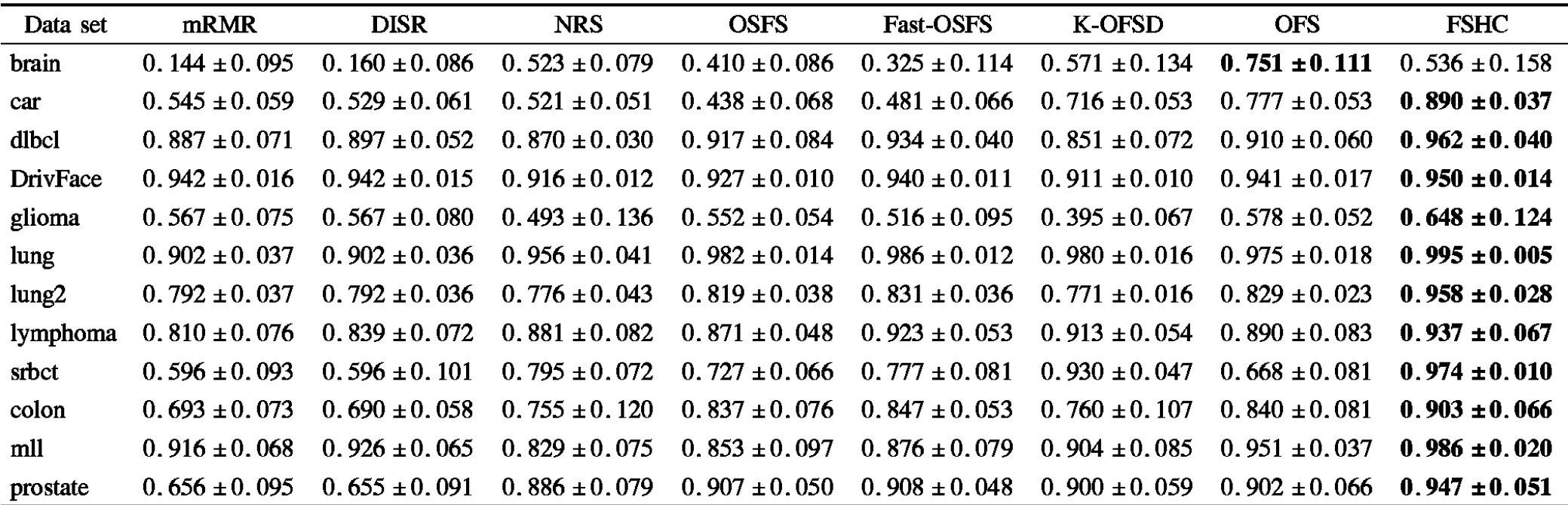
表5 平均分类精度和标准差Table 5 Average classification accuracy and standard deviation
3.4.2 统计性分析
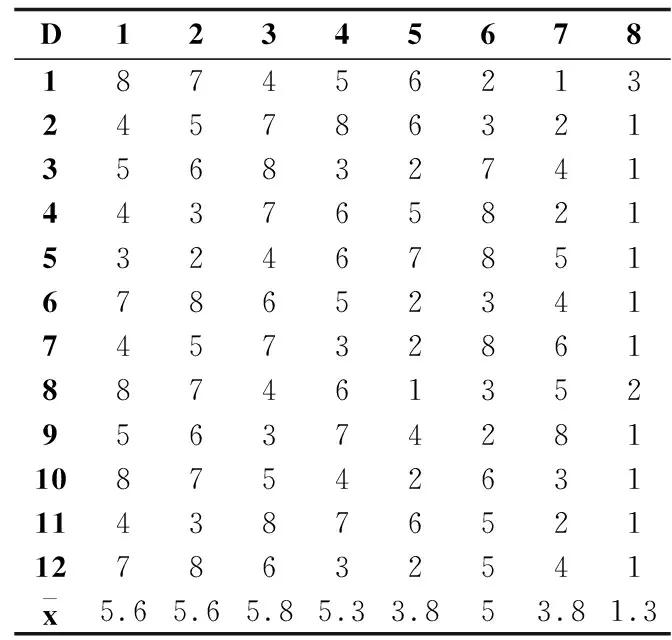
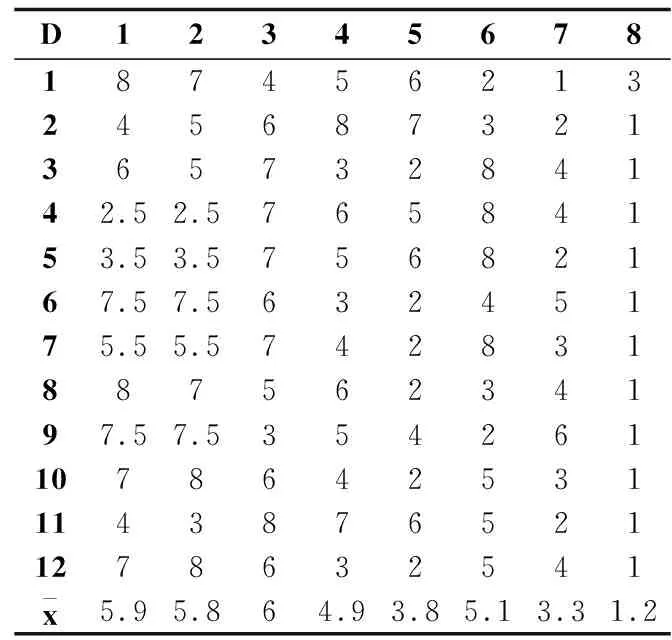
序值表6中的子表(a)-(c)分别根据表3-表5的测试结果给出了多数据集多算法在F-Score、G-Mean和分类精度评价指标上的算法比较序值表,各算法在每个数据集上根据测试性能由好到坏排序,并赋予序值,若算法的测试性能相同,则平分序值.表6横轴的数字对应表3的表头横轴代表的算法,纵轴的数字对应表3的表头纵轴代表的数据集,其中,最后一行表示各算法的平均序值.对表F检验参数alpha取0.05的常用临界值表可知,8个算法12个数据集的临界值为2.131,根据Friedman统计量公式,计算F-Score、G-Mean、分类精度的τF值分别为7.934、6.998、9.299,均大于F检验临界值2.131,拒绝“所有算法性能相同”的假设,进行Nemenyi后续检验.对表Nemenyi检验参数alpha取0.05的常用qα值表可知,8个比较算法的qα值为3.031,根据Nemenyi检验的临界值域公式,计算得到临界值域CD为3.031.
由表6的平均序值可知,子表(a)、(b)、(c)算法FSHC与算法Fast-OSFS 、OFS的差距均未超过临界值域,说明算法FSHC与算法Fast-OSFS 、OFS的性能没有显著差别.而算法FSHC显著优于算法mRMR、DISR、NRS、OSFS、K-OFSD,因为算法FSHC与算法mRMR、DISR、NRS、OSFS、K-OFSD的差距超过了临界值域.
上述比较检验可以直观地用弗里德曼检验图显示,图3中的子图(a)-(c)的弗里德曼检验图分别由表6中的子表(a)-(c)导出,横轴表示各算法的平均序值,纵轴表示算法,对应表6的算法序号,其中,第8号纯黑线表示算法FSHC的平均序值和临界值域.对每个算法,用圆点显示其平均序值,以圆点为中心的横线段表示临界值域的大小,于是可从图中观察,若两个算法的横线段有交叠,说明这两个算法的分类性能没有显著差别,否则说明其性能有显著差别.也可以用灰度区分算法的性能,第8号纯黑线为算法FSHC,对比其余算法,对比算法为深灰线,说明性能显著不同,对比算法为浅灰线,说明性能没有显著差别.由图3可见,子图(a)、(b)、(c)纯黑线8号算法FSHC与浅灰线5号算法Fast-OSFS 、7号算法OFS没有显著差别,因为它们的横线段有交叠区域,对比算法灰度为浅灰,而算法FSHC显著优于余下的算法,因为它们的横线段没有交叠区域,余下对比算法灰度为深灰.显然,算法FSHC的平均序值均高于对比算法,说明FSHC的分类性能均优于对比算法.
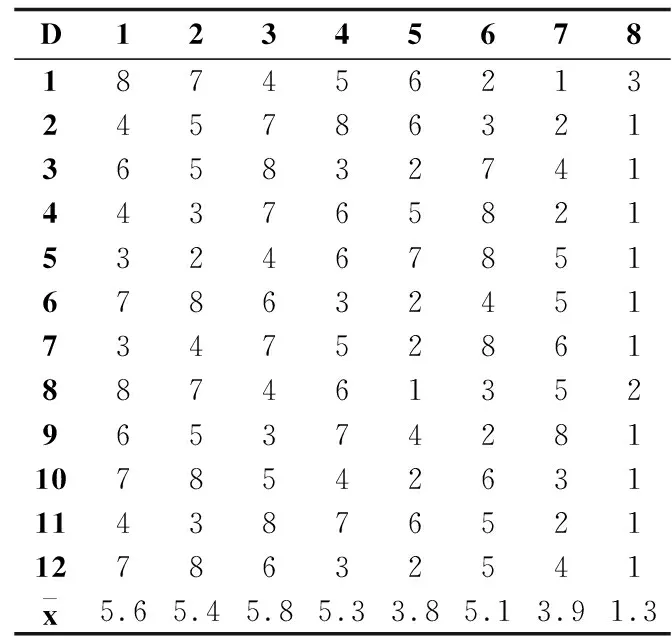
表6 算法比较序值表Table 6 Ordinal table of algorithm comparison
(b)G-Mean index
(c)Accuracy index
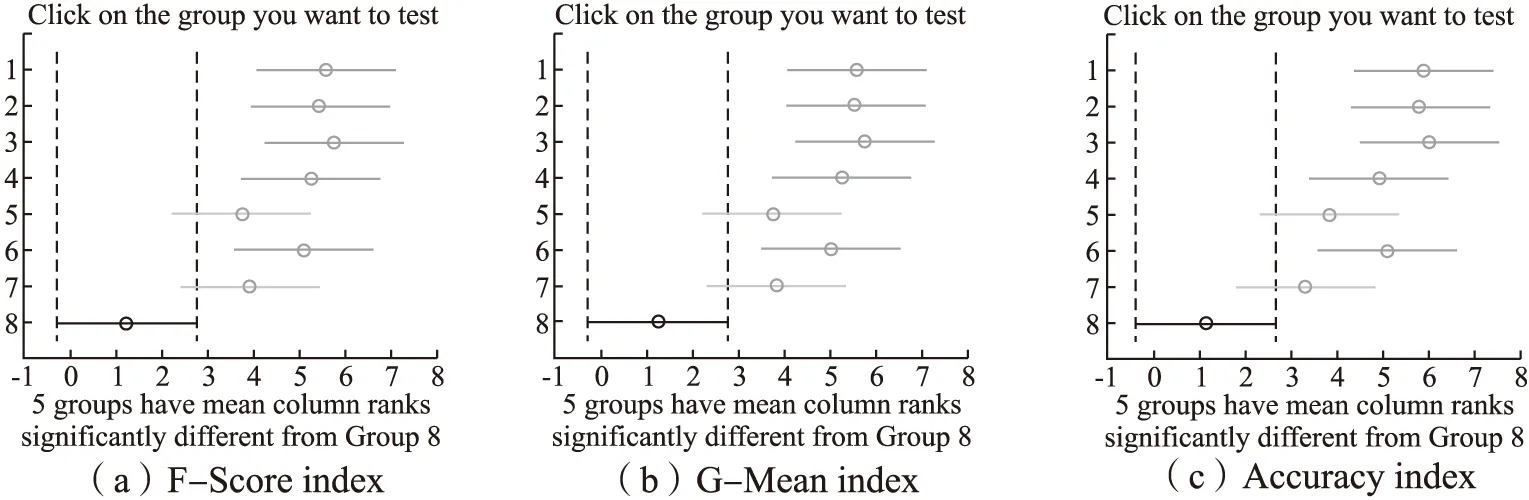
图3 FSHC算法与对比算法的Friedman检验图Fig.3 Friedman test diagram of FSHC algorithm and comparison algorithms
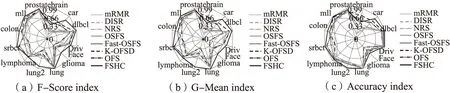
图4 FSHC算法与对比算法的蜘蛛网图Fig.4 Spider diagram of FSHC algorithm and comparison algorithms
3.4.3 稳定性分析
为了验证不同算法的稳定性[15],绘制蜘蛛网图来表示多数据集多算法在各个评价指标上的稳定性指数.图4中的子图(a)-(c)分别给出了算法在F-Score、G-Mean和分类精度评价指标上的稳定性指数,其中,纯黑直线代表算法FSHC的稳定性值.由图4可见,对于F-Score和G-Mean而言,算法FSHC在6个数据集上接近稳定解,在类别不平衡数据集brain、DrivFace、glioma、lymphoma上稳定性较弱.
4 结束语
在高维类别不平衡数据特征选择过程中,为了获得在小类样本中具有高可分离性的特征,通过定义样本的近邻关系,计算样本分布与类别空间的包含度,进而导出特征与标记的一致性,由此提出一致性分析模型,并构建了面向高维类别不平衡数据的贪婪搜索算法.实验结果表明,本文所提的方法是有效的.

