基于Matlab的电阻炉温度控制系统设计及仿真比较

夏百花，韦 颖，方 飞

（安徽三联学院 电子电气工程学院，安徽 合肥 230601）

电阻炉是热处理工艺过程中应用最广、数量最多的电加热设备。随着控制技术日新月异的发展，对电阻炉温度控制的要求也就越来越高。电阻炉是利用电流通过电热体元件将电能转化为热能来加热或熔化工件和物料的热加工设备，其温度控制具有单向性、大惯性、大滞后等复杂特点，主要分为升温、保温和降温3个部分，其中，升温、保温依赖电阻丝加热完成，而降温则主要依靠自然环境进行冷却。

1 系统框架

电阻炉温度控制系统多采用闭环控制，首先，将电阻炉实际温度值通过温度传感器测量出来；其次，通过负反馈与设定温度进行比较得到偏差信号，送入控制器中得到控制信号，控制可控硅，以此改变电阻丝的加热电流或电压，从而实现电阻炉的温度控制[1]。系统框架如图1所示。

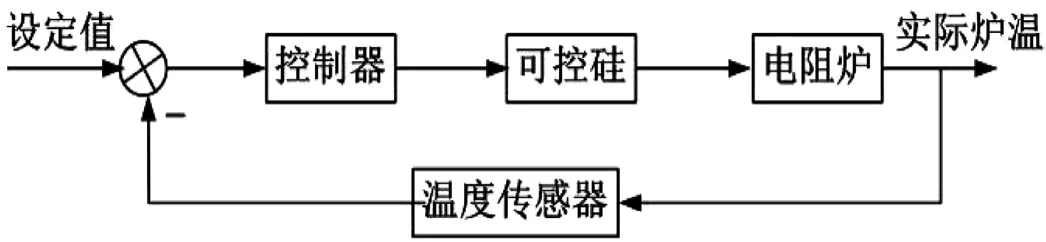
图1 电阻炉温度控制系统框架

本文主要是采用传统PID控制、Smith控制和模糊控制3种算法实现对电阻炉温度的控制，并进行仿真及对仿真结果的比较分析。

2 控制算法比较

理论分析和实验结果表明，均将电阻炉当作具有自平衡能力且存有滞后的被控对象，因此其数学模型可用一阶惯性和纯滞后两个环节进行描述，系统总的传递函数为：

2.1 不加控制器仿真

不外加控制器的仿真模型控制如图2所示，其仿真结果如图3所示，可以看出，此系统具有100 ms的延迟，并且在仿真时间内仅上升到了70°左右（设定值为100°），且调节时间较长。

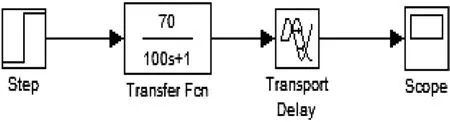
图2 不加控制器的系统仿真模型

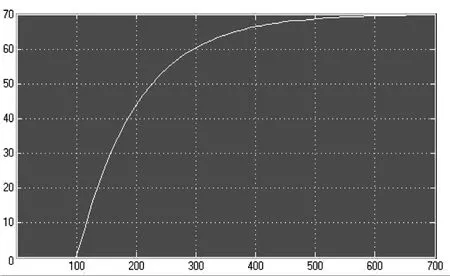
图3 不加控制器的仿真结果

2.2 PID控制器仿真

PID控制器所采用的控制规律为比例、积分、微分控制，控制规律如图4所示。

图4 PID控制原理

其PID控制器的输入与输出之间的关系为：

对于此系统，在笔者有限的经验范围内，未找到使系统稳定的合适PID值。虽然PID控制器凭借结构简单、参数调整方便等诸多优点应用于大多数控制系统中，但在此系统中延迟较大，难以实现对温度的控制[2]。

2.3 Smith预估控制算法仿真

Smith预估控制算法是一种针对大时间滞后系统进行补偿的常用方法。图5为Kp=0.7，KI=0.16，Td=1.3时的Smith控制系统仿真结果。

可以看出，该控制方法超调量较大，动态过程调节时间较长。但在此系统中，当其温度一旦出现超调量，就无法采用控制手段来降温，因而应用传统的控制理论和控制方法难以达到理想的控制效果[3]。

2.4 模糊控制算法仿真

智能控制方案是一类无需人为干预就能够针对控制对象的状态自动调节控制规律，以实现控制目标的控制策略。它和常规控制理论不同的地方在于：（1）不需要建立精确的数学模型。（2）不需要进行定量计算与困难性分析。它是一种无模型控制方案，即在不知道对象精确模型的情况下，在自我的调节作用下，使得实际响应曲线近似于理想响应曲线[4]。

模糊控制是智能控制的一个重要分支，本设计采用的模糊控制器采用两输入一输出的控制方法，其中输入为表示温度误差E和误差变化率EC，输出为控制加热的供电电压U，均为模糊变量。

此系统输入为单位阶跃信号，选取量化因子Ke=0.7，Kec=0.05，比例因子Ku=0.02，建立如图6所示模糊控制系统，其Matlab仿真结果如图7所示。可以得出，系统在整个响应过程中未出现超调现象，且动态调节时间减小。

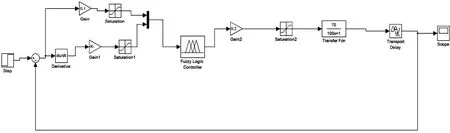
图6 模糊控制系统仿真模型

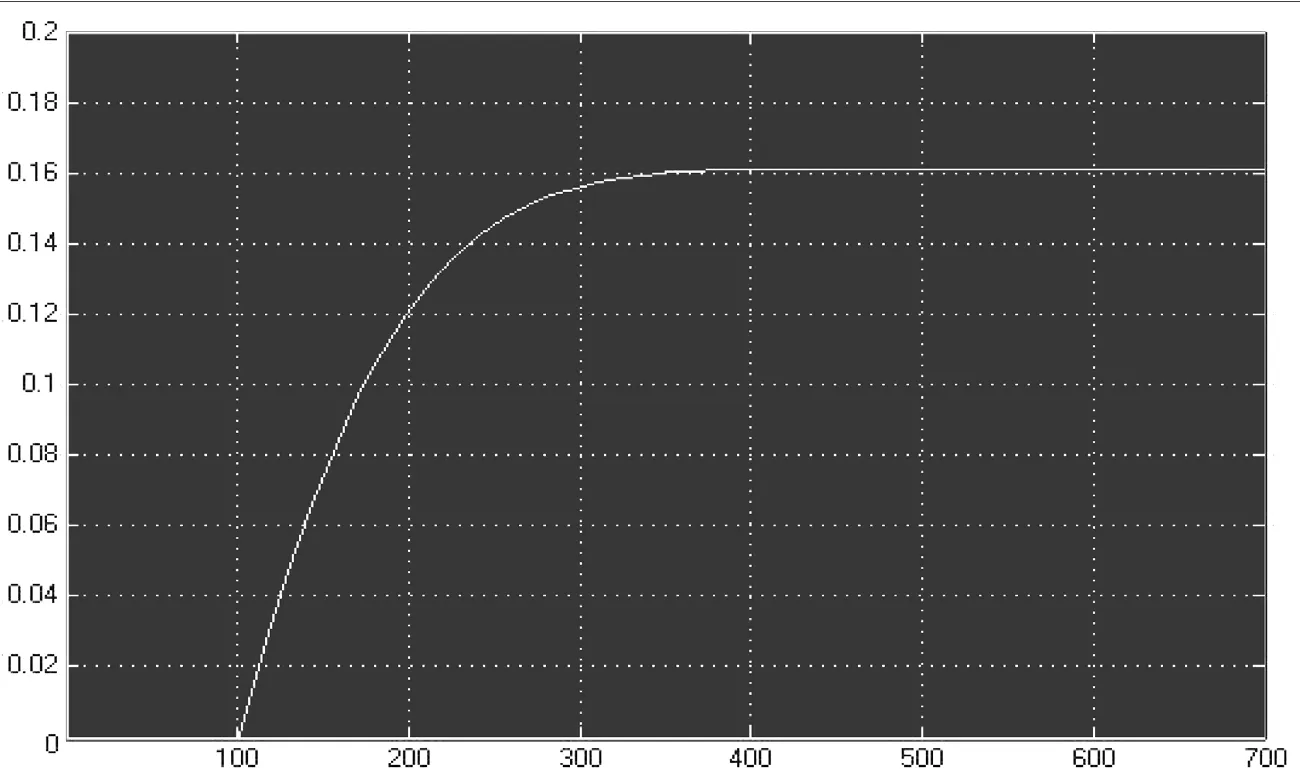
图7 模糊控制系统仿真结果

3 结语

对于一个纯滞后时间较长且不允许出现超调的电阻炉温度控制来说，由于系统本身是一个自衡系统，虽能最终到达稳定状态，但调节时间较长；而对于常规PID控制来说，比例、积分和微分3个参数不易找到，故不选用此算法；广泛适用于滞后系统的Smith预估算法虽然也能稳定，但其算法中需要知道被控对象的准确数学模型，故不选用此方法；由于电阻炉本身结构较为复杂，其数学模型很难得到，当采用模糊控制时，整个系统的调节时间较小，且没有出现超调现象，故选用此方法。