数据挖掘在全国计算机等级考试(NCRE)成绩分析中的研究及应用

徐承俊 朱国宾

(武汉大学遥感信息工程学院 湖北 武汉 430079)

0 引 言

信息化的发展使得计算机的作用越发凸显，也改变着我们的生活方式。在我国，绝大部分企业、高校等，尤其是大专类院校，把计算机等级证书作为学生是否真正掌握计算机实际操作的衡量标准，要求学生毕业前尽可能获得全国计算机一、二级证书。但从考试实际情况看仍存在优秀率低、高级别通过率低等问题。这些问题引起了学校、学院的高度重视，同时也令老师和学生感到很困惑。老师无法从考生成绩中找到规律性的原因，学生则很难进行针对性复习和应考。事实上，从一个庞大且复杂的数据中挖掘隐藏的数据信息，需要采用新的方法和技术，而数据挖掘技术无疑是目前最为有效的方法。

国外对数据挖掘的研究起步早，发展快。近些年主要研究集中在：(1) 天文系统，如加州理工学院计算机专家与天文学家共同开发的天文SKICAT系统[1]；(2) 金融行业，如金融系统中甄别洗钱FAIS系统[2]；(3) 零售行业，如超市销售异常情况分析OPPORTUNITYEXPLORER系统[3]等。但这些研究几乎不涉及对影响考试成绩因素的挖掘。

国内高校主要将数据挖掘应用于高校教学与管理，如北京市科学技术委员会重点课题《教育考试数据挖掘的研究与实现》[4]，挖掘教育考试数据内在关联；将教育数据挖掘应用于招生、就业、后勤服务等各方面[5]。

以上研究主要涉及行业研究，很少有学者对某一具体考试中影响成绩合格、优秀等因素展开研究。本文提出基于数据挖掘关联规则Apriori算法和C4.5算法相结合建立考试成绩分析模型，建立学生对课程的热爱程度、课前预习、课后复习和各种题型与成绩的关联，以2016年考试数据为训练集，2017年考试数据为测试集，根据实际成绩进行对比论证。挖掘导致优秀率低、高级别通过率低的原因，并将得到的信息反馈给教师，以提高教学效率，查漏补缺，提高考试优秀率和高级别类通过率。

1 技术路线

1.1 Apriori

本文针对不同专业的考生成绩和各种题型，如单选题、基本操作题、OFFICE操作题(Word，Excel，PPT)、上网操作题得分为目标，分析其内在的关联，挖掘出各类题型得分对成绩不合格、合格和优秀的影响。基于这些关联，本文采用关联规则Apriori算法[6]，伪代码如下：

L1 =fINd_frequent_1-itemsets(D);

//找出频繁1项集

FOR(k=2;Lk-1 !=null;k++){

//产生候选，并剪枝

Ck =apriori_gen(Lk-1 );

//扫描D进行候选计数

FOR each 事务t IN D{

Ct =subset(Ck,t);

//得到t的子集FOR each 候选c属于Ct

c.count++;}

//返回候选项集中不小于最小支持度的项集

Lk ={c 属于 Ck | c.count>=mIN_sup}}

RETURN L= 所有的频繁集；

第一步：连接(joIN)

Procedure apriori_gen(Lk-1 :frequent(k-1)-itemsets)

FOR each 项集 l1 属于 Lk-1

FOR each 项集 l2 属于 Lk-1

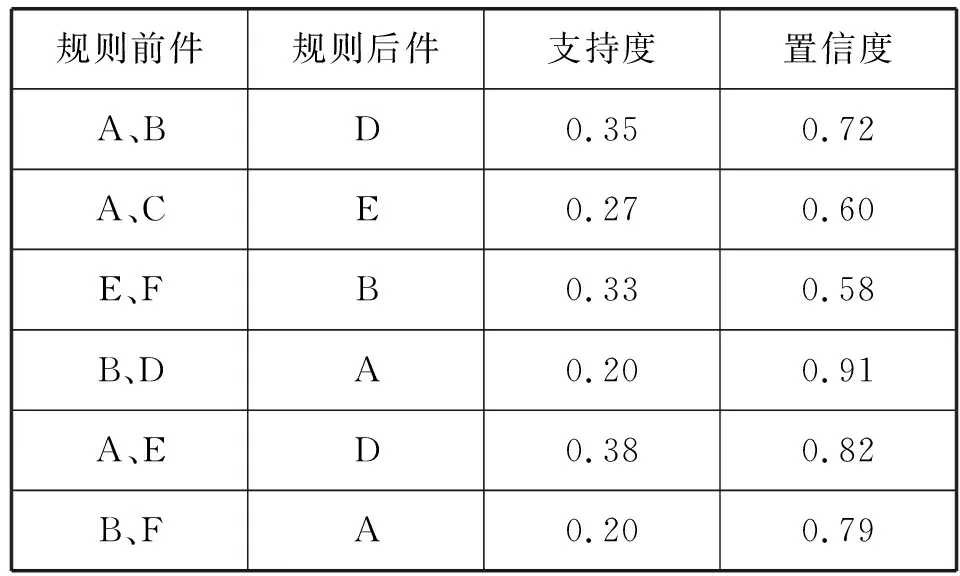
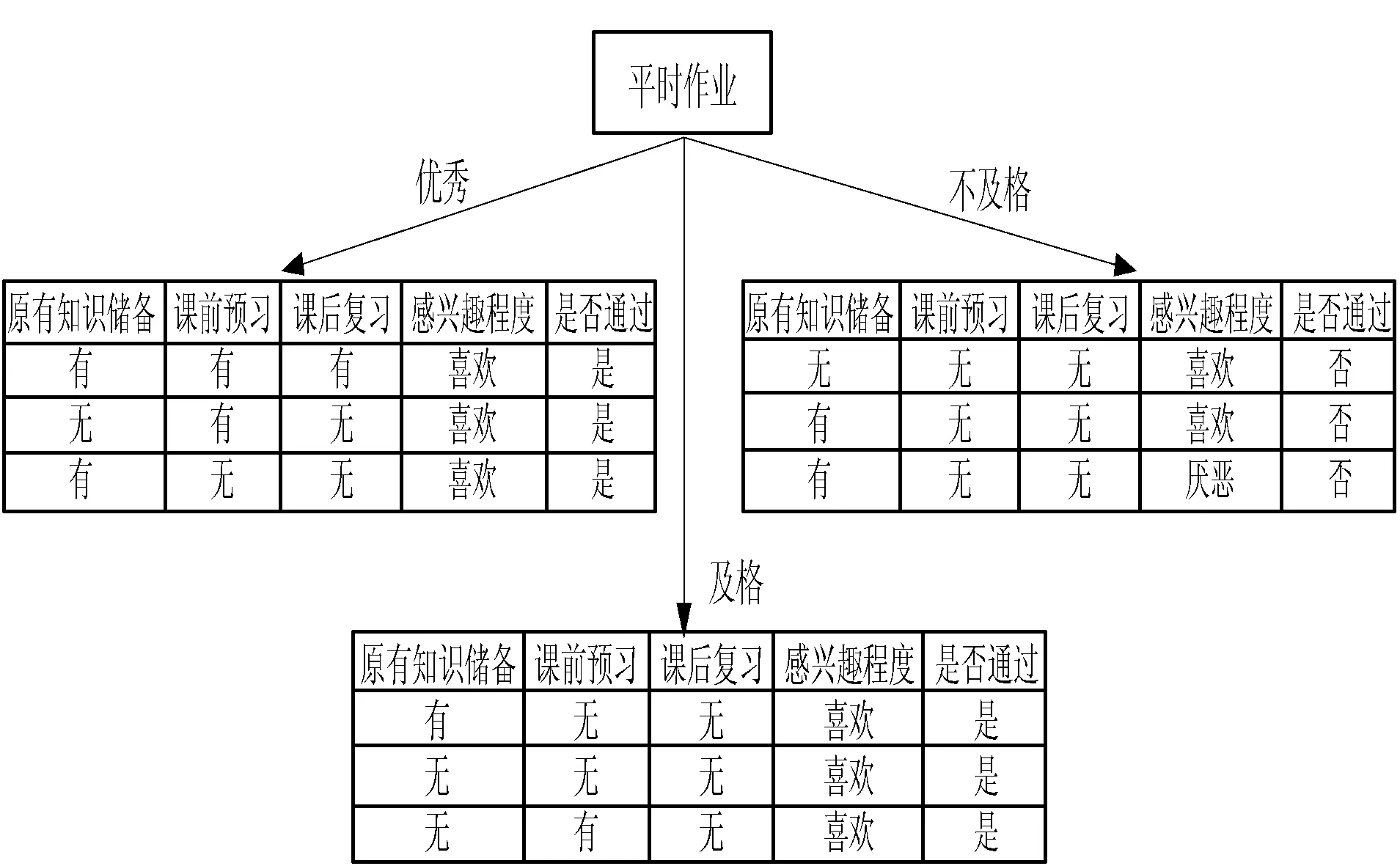
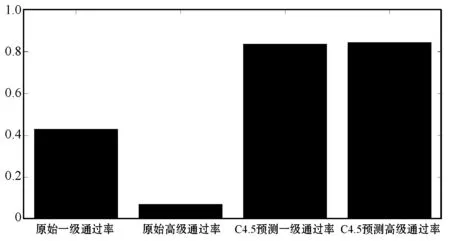
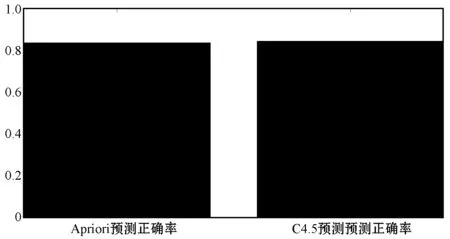
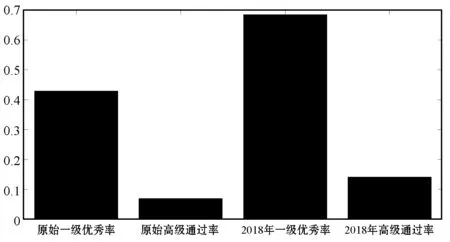
IF( (l1 [1]=l2 [1])&&( l1 [2]=l2 [2])&& ……&& (l1 [k-2]=l2 [k-2])&&(l1 [k-1]

THEN{

c = l1 连接 l2

//连接步：产生候选

//若k-1项集中已经存在子集c则进行剪枝

IF has_INfrequent_subset(c, Lk-1 ) THEN

delete c;

//剪枝步：删除非频繁候选

else add c to C}

RETURN Ck;

第二步：剪枝(prune)

Procedure has_INfrequent_sub(c:candidate k-itemset;Lk-1: frequent(k-1)-itemsets)

FOR each (k-1)-subset s of c

IF s 不属于 Lk-1 THEN

RETURN true;

RETURN false;

1.2 C4.5

Apriori算法每轮迭代都要扫描数据集，因此在数据集很大、数据种类很多的情况下，算法效率很低。本文引入C4.5算法，其具有如下优点：(1) 效率高。数据计算量小，减少因计算而花费的时间和精力，提高效率。(2) 便于客户理解。研究结果既反馈给教师，又反馈给学生，对其理解和解析所需的专业背景知识要求低。树形结构简单易懂，简单的IF语句即可实现。(3) 数据类型灵活。既能对离散数据，又能对连续数据进行处理。(4) 结构清晰。

从“学生对该课程的热爱程度”、“课前预习、课后复习”、“课堂上机实践完成程度”和“学前原有知识储备”等多个方面来分析构造决策树。将两种算法有机结合，更具有普遍性，使得数据分析结果更具有说服力。

C4.5算法伪代码如下[7]：

训练样本集D={(x1,y1),(x2,y2),…,(xn,yn)}

属性集A={a1,a2,…,an}

TreeGenerate(D,A):

//生成节点node

IF D中样本全属于同一类别C:

将node标记为C类叶节点

RETURN

END IF

IF 属性集A为空或者D的所有属性值均一样:

将node标记为最多类

RETURN

END IF

从A中选取最佳划分属性a*

FOR a IN a*:

为node生成一个分支，令Dv表示D中在a*属性值为a的样本子集

IF Dv为空:

contINue;

else:TreeGenerate(Dv,A{a*})递归继续

END IF

END FOR

2 算法实现

2.1 Apriori关键计算

关联规则的支持度(support)为：

support(A⟹B)=P(A∪B)

关联规则的置信度(confidence)为：

confidence(A⟹B)=

P(B|A)=support(A∪B)/supportA=

support_count(A∪B)/support_count(A)

项集的出现频度(support_count)：包含项集的事务数，即为项集的计数。

根据上述公式，找出所有的频繁项集以及由频繁项集产生强关联规则。

关联规则如表1所示。其中：A代表单选，B代表基本操作，C代表Word操作，D代表Excel操作，E代表PPT操作，F代表上网操作，G代表总成绩。

表1 关联规则表

结果分析：

① 单选和基本操作同时为优秀，总成绩有72%优秀可能。

② 单选和Word操作同时为优秀，总成绩有60%优秀可能。

③ PPT和上网同时为优秀，总成绩有58%优秀可能。

④ 基本操作和Excel同时为优秀，总成绩有91%优秀可能。

⑤ 单选和PPT同时为优秀，总成绩有82%优秀可能。

⑥ 基本操作和PPT同时为优秀，总成绩有79%优秀可能。

可以发现，考生在Word、Excel和PPT三种题型上的表现对考试总分的影响较大。

2.2 C4.5关键计算

信息增益公式：

式中：D表示训练集；k表示类的不同属性的取值数；pi是训练集D中任意元素在k个类的不同属性所占的比率。Info(D)也称为D的熵。

信息增益率公式为：

splitRatio(A,D)=[Split(A,D)-Info(A,D)]/

Split(A,D)

式中：Split(A,D)表示属性A对D的分裂信息量；splitRatio(A,D)表示属性A对D的分裂信息量的变化率。用信息增益率最大的作为决策树根，因“平时成绩”有最大信息增益率，故将其作为根节点，对每个属性建立分支并生产决策树，得到如图1所示决策树。

图1 部分数据的决策树

结果分析：

① IF(“原有知识储备”=“无”)&&(“课前预习”=“无”)&&(“课后复习”=“无”)&&(“感兴趣程度”=“喜欢”)then “是否通过”=“否”。

② IF(“原有知识储备”=“有”)&&(“课前预习”=“无”)&&(“课后复习”=“无”)&&(“感兴趣程度”=“喜欢”)then “是否通过”=“否”。

③ IF(“原有知识储备”=“有”)&&(“课前预习”=“无”)&&(“课后复习”=“无”)&&(“感兴趣程度”=“厌恶”)then “是否通过”=“否”。

④ IF(“原有知识储备”=“无”)&&(“课前预习”=“无”)&&(“课后复习”=“无”)&&(“感兴趣程度”=“厌恶”)then “是否通过”=“否”。

可以发现，“平时成绩”对考试是否通过影响比较大，“课后巩固”也很重要。

3 讨论及分析

本文以2016年考试数据为训练集，对2017年考试数据预测，结果如图2、图3所示。

图2 实际成绩与Apriori预测对照图

图3 实际成绩与C4.5决策树预测对照图

如图2所示，应用Apriori对1 200名考生的考试成绩进行预测，发现1 002名考生数据正确，198名考试数据错误，实际考试通过率为83.5%。

如图3所示，应用决策树对1 200名考生的考试成绩进行预测，发现1 013名考生数据正确，187名考试数据错误，实际考试通过率为84.4%。

Apriori算法与C4.5算法预测对比如图4所示。可以看出，C4.5算法准确度要比Apriori算法略高一些，因为在实际考试中，基于Apriori算法中各个题型得分由考生掌握知识点程度决定，得分相对稳定，但是考试过程中的状态，例如预习、复习时间长短、复习效率都易受到情绪波动影响，C4.5算法预测会有一些波动，但只影响其预测值。两个算法预测值基本相同，由此可见，两个算法总体上的可信度是可取的。

图4 Apriori算法与C4.5算法预测对比图

基于上述模型分析，挖掘出导致考试一级优秀率低和高级别通过率低原因：(1) 各类题型作答优秀直接影响考试优秀率；(2) 自身主观原因，如“课前预习”“课后复习”“感兴趣程度”等都是导致通过率、优秀率低的原因。将这些信息反馈给教师和学生。在教师层面，教师对学生因材施教，培养学生自主学习的良好习惯，保持良好的学习态度和方法。在学生层面，学生可以通过决策树分析自己在学习过程中的问题，并结合关联规则的相关结论，把握各题型的作答重点，有针对性地进行训练操作。

将本文方法应用于2018年全国计算机等级考试，优秀率、通过率对比如图5所示。可以看出，该方法使得一级优秀率平均提升25%，高级通过率平均提升50%。

图5 2018年全国计算机等级考试优秀率、通过率对比图

4 结 语

本文主要以2016年、2017年考生成绩库为研究基础，从以下两个方面分析：(1) 从题型入手，采用基于Apriori算法针对不同的题型，找出它们之间的关联规则，发现题型本身的关联及影响；(2) 基于C4.5决策树，以学生“原有知识储备”、“课前预习”“课后复习”“感兴趣程度”等为切入点，构建决策树模型，找到考生不合格的原因。通过两种算法的研究和分析，挖掘出隐含在考试数据库信息，并将研究结果反馈给授课教师及学生。实验结果表明，本文方法能够有效提高全国计算机等级考试通过率及优秀率。