基于主成分分析的船舶操纵性综合评价
闫成勇 章文俊 尹建川 王平林 薛宗耀


摘要:针对船舶操纵性评价过程中存在的评价指标权重确定主观性强和分配不统一等问题,提出一种基于主成分分析(principal component analysis, PCA)的船舶操纵性综合评价方法。该方法以国际海事组织(International Maritime Organization, IMO)船舶操纵性指标为基准,根据操纵性指标的主成分贡献率确定指标权重,客观地算出船舶操纵性综合评价值。通过对8艘船的操纵性试验数据进行分析计算,得到每艘船的船舶操纵性综合评价值。结果表明,该方法不仅在理论上科学、客观,而且在实际应用中简单、可靠,有助于提高船舶操纵性综合评价的客观性。
关键词: 船舶操纵性; 主成分分析(PCA); 综合评价
中图分类号: U661.33 文献标志码: A
Comprehensive evaluation of ship maneuverability
based on principal component analysis
YAN Chengyong, ZHANG Wenjun, YIN Jianchuan, WANG Pinglin, XUE Zongyao
(Navigation College, Dalian Maritime University, Dalian 116026, Liaoning, China)
Abstract: Aiming at the problems of the stronger subjectivity of evaluation index weight determination and the inconsistence of weight distribution in the evaluation of ship maneuverability, a comprehensive evaluation method of ship maneuverability based on the principal component analysis (PCA) is proposed. The IMO ship maneuverability indexes are taken as evaluation indexes, the weights of indexes are determined according to their principal component contribution ratios, and the comprehensive evaluation value of ship maneuverability is calculated objectively. By analyzing and calculating the maneuverability experimental data of eight ships, the comprehensive evaluation value of each ship is obtained. The results show that, the method is not only scientific and objective in the theory, but also simple and reliable in the practical application. It is helpful to improve the objectivity of comprehensive evaluation of ship maneuverability.
Key words: ship maneuverability; principal component analysis (PCA); comprehensive evaluation
0 引 言
船舶航行安全一直是人們关注的重点,船舶操纵性与船舶航行安全密切相关,因此船舶操纵性评价也备受关注。国际海事组织(International Maritime Organization, IMO)第MSC.137(76)号决议[1]明确给出了关于船舶操纵性指标(旋回能力、初始旋回能力、偏航纠正和航向稳定能力和停船能力)的规定。船舶操纵性评价是一个多指标系统评价问题,过去对船舶操纵性评价多基于单项指标,只能反映船舶某一方面的操纵性能,不够全面。目前有关操纵性评价的研究如下:文献[2]基于层次分析法重点考虑船舶保向性和初始旋回性,对大型船舶的操纵性能进行了综合排序;文献[3]使用了灰关联分析和逼近理想解法评价船舶操纵性;文献[4]基于熵权法和模糊集对船舶操纵性进行了综合评价;IMO《船舶操纵性标准》给出了各船舶操纵性指标的最低要求;美国船级社(American Bureau of Shipping, ABS)出版的《船舶操纵性准则》[5],在IMO《船舶操纵性标准》基础上将各类指标分为5个等级,1级对应IMO船舶操纵性指标要求;文献[6]将神经网络运用于船舶操纵性评价,主要研究了旋回试验和Z形试验;文献[7]提出计算流体力学(computational fluid dynamics, CFD)方法在浅水区船舶操纵性评估中的应用;文献[8]利用非线性瞬态操纵模型与数学规划技术的耦合评估船舶操纵性能;文献[9]结合ABS《船舶操纵性准则》,利用模糊网络分析法对船舶操纵性进行了评价。这些评价方法中存在评价指标权重分配不统一等人为不确定性和评价指标不全面等问题。主成分分析 (principle component analysis, PCA)法能很好地解决评价指标权重分配问题,已被广泛应用于交通拥堵研究[10]、沿海港口类型化研究[11]等工作中。本文在前人研究的基础上,将PCA法引入船舶操纵性综合评价中,客观地确定各评价指标权重,使评价结果更加客观、合理。
1 船舶操纵性综合评价指标
IMO第MSC.137(76)号决议《船舶操纵性标准》体现了船舶操纵性对航行安全的重要作用,为主管机关制定与执行船舶操纵性标准提供具体指导,有助于提高海上安全和加强对海洋环境的保护。船舶操纵性指标包括以下4种[12]:
旋回能力。它用来衡量船舶满舵时的机动回转能力。通过实船回转试验数据确定旋回能力:当船舶进入偏航率为零的稳定状态后,将舵操至右舷和左舷35°舵角或至试验速度下许用的最大舵角;旋回操纵时,进距(Ad)应不超过4.5L(L为船长),旋回初径(Td)应不超过5L,数据越小说明旋回性越好。
初始旋回能力。它用来衡量船舶在直航时改变航向的能力,反映船舶对中等舵角的反应能力。通过实船试验,当船舶进入偏航率为零的稳定状态后,船舶向左或向右操10°舵角,当船首向改变10°时,记录船舶在原航向上前进的距离L10。用L10衡量初始旋回能力,L10越小初始旋回能力就越好。
偏航纠正和航向稳定能力。它用来衡量船舶控制航向的能力。它指当船舶进入旋回状态且角速度达到一定值时向旋回相反方向操舵,船首向对舵的反应能力。一般采用通过船舶Z形试验获得的超越角θ来衡量,θ越小航向稳定性越好。
停船能力。停船能力是一个衡量船舶运动惯性的指标。通过全速倒车试验数据判定停船能力:船舶在全速进车航行中进行全速倒车操作,直到船舶速度为0时,记录船舶在原航向的纵向前进距离Ds。用Ds衡量停船能力,Ds越小船舶停船性能越好。
2 基于PCA的船舶操纵性综合评价模型 PCA法是1901年Pearson针对非随机变量引入的,1933年Hotelling将此方法推广到随机向量,1965年Massy提出主成分估计,它是回归系数的一种有偏估计,是为了克服最小二乘(least squares, LS)估计在设计阵病态(即存在多重共线性)时表现出的不稳定而提出的。PCA将相关性强的变量转化成彼此不相关的变量,用较少的变量去解释原来大部分变量,用于综合评价。[13]
2.1 PCA法的步骤
(1)原始数据的标准化处理。为去除指标量纲的影响,在计算前对数据进行标准化处理。假设指标变量有m个(x1,x2,…,xm),共有n个评价对象,第i个评价对象的第j个指标的取值为xij,将指标值xij转换成x ~ij,x ~ij=xij-x-ijsj (i=1,2,…,n; j=1,2,…,m) 其中:x-j=1nni=1xij,sj=1n-1ni=1(xij-x-j)2,即x-j和sj分别为第j个指标的样本平均值和样本标准差。对应地,指标化指标变量如下:x ~j=xj-x-jsj (j=1,2,…,m) (2)确定相关系数矩阵R。用相关系数对指标变量进行相似性度量,相关系数矩阵R=(rjk)m×m,其中rjk=ni=1(x ~ij×x ~ik)n-1 (j, k=1,2,…,m) 式中:rjj=1,rjk=rkj,rjk是第j个指标与第k个指标的相关系数。
(3)计算特征值和特征向量。计算相关系数矩阵R的特征值,λ1≥λ2≥…≥λm≥0,以及对应的特征向量μ1,μ2,…,μm,其中μj=(μ1j,μ2j,…,μnj)T,由特征向量组成m个新的指标变量y1=μ11x ~1+μ21x ~2+…+μn1x ~n
y2=μ12x ~1+μ22x ~2+…+μn2x ~n
…
ym=μ1mx ~1+μ2mx ~2+…+μnmx ~n式中:y1,y2,…,ym分别是第1, 2,…, m主成分。
2.2 船舶操縱性评价模型的建立
选择p(p≤m)个主成分,计算综合评价值。
(1)计算特征值λj(j=1,2,…,m)的信息贡献率和累积贡献率。主成分yj的信息贡献率bj=λjmk=1λk (j=1,2,…,m) 主成分y1,y2,…,yp的累积贡献率Δp=pk=1λkmk=1λk若Δp接近1,则选择前p个指标变量y1,y2,…,yp作为p个主成分,代替原来m个指标变量,从而对p个主成分进行综合分析。
(2)计算主成分载荷。主成分载荷反映主成分yj与原变量xj之间的相互关联程度,原变量xj(j=1,2,…,m)在主成分yi(i=1,2,…,p)上的载荷
L(yi,xj)=μijλi
(i=1,2,…,p; j=1,2,…,m)
(1)
(3)计算综合得分:Z=pj=1(bjyj)pj=1bj (j=1,2,…,p) 根据综合得分就可进行综合评价。
3 模型检验
3.1 基于PCA的评价流程及算例
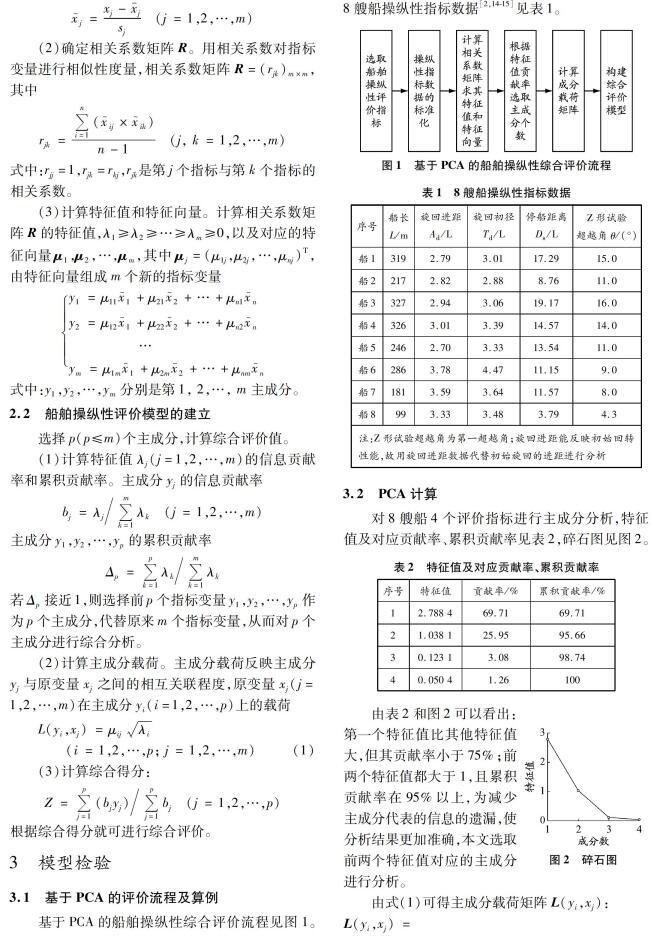
基于PCA的船舶操纵性综合评价流程见图1。8艘船操纵性指标数据[2,14-15]见表1。
3.2 PCA计算
对8艘船4个评价指标进行主成分分析,特征值及对应贡献率、累积贡献率见表2,碎石图见图2。
由表2和图2可以看出:第一个特征值比其他特征值大,但其贡献率小于75%;前两个特征值都大于1,且累积贡献率在95%以上,为减少主成分代表的信息的遗漏,使分析结果更加准确,本文选取前两个特征值对应的主成分进行分析。
由式(1)可得主成分载荷矩阵L(yi,xj):
L(yi,xj)=
-0.862 60.436 0 0.254 1 0.036 0
-0.784 50.572 5-0.238 2 0.011 8
0.779 10.608 7 0.042 8-0.143 8
0.906 60.387 1-0.001 1-0.168 1
通过载荷矩阵看出:第一主成分能解释4个原始指标,尤其是旋回能力指标和停船能力指标;第二主成分是对第一主成分的补充,特别体现在初始旋回能力指标和偏航纠正和航向稳定能力指标上。
为了更好地分析和理解,利用MATLAB对每一主成分和操纵性指标进行画图展示。在极坐标系中,图3代表一个四维空间,每个同心圆代表一个主成分(用对应的特征向量μj表示),半径最大的代表第一主成分,其他以此类推;与圆相交的4根轴分别代表4个船舶操纵性指标;每个小圆代表相应特征向量的分量,其半径大小由其在相应特征向量内所占比例确定,半径大小也表明主成分与相应分量的相关性。[16]
μ1=(-0.516 6,-0.469 8, 0.466 6, 0.542 9)T
μ2=(0.427 9, 0.561 9, 0.597 4, 0.379 9)T
μ3=(0.724 1,-0.678 9, 0.121 9,-0.003 2)T
μ4=(0.160 5, 0.052 6,-0.640 7, 0.748 9)T
鉴于前两个特征值的累积贡献率达到95%以上,结合主成分载荷矩阵,可以看出前两个主成分分析效果较好。两个特征值对应的主成分分别为
y1=-0.516 6x ~1-0.469 8x ~2+
0.466 6x ~3+0.542 9x ~4
(2)
y2=0.427 9x ~1+0.561 9x ~2+
0.597 4x ~3+0.379 9x ~4
(3)
把各船4个指标的标准化数据代入式(2)和(3),得到各船的两个主成分值,如矩阵Y所示。Y=1.809 90.174 9
0.521 2-1.374 3
1.887 10.719 3
0.768 40.406 3
0.710 9-0.409 2
-2.260 01.539 4
-1.332 40.357 8
-2.105 1-1.414 1 分别以两个主成分的贡献率为权重,构建船舶操纵性综合评价模型:Z=0.697 1y1+0.259 5y20.956 6
(4) 把各船的两个主成分值代入式(4),得到各船操纵性综合评价值及排序结果(见表3),综合评价值越小,船舶操纵性越好。
从表3可以看出,船8的操纵性最好,船3的操纵性最差。
为进行对比分析,选择常用的层次分析法进行对比试验。层次分析法是一种定性分析与定量分析相结合的决策方法,它将一个复杂的决策问题分解为多指标多层次问题,用决策者的经验判断各目标之间的相对重要程度,再利用数学方法确定每一层次的权重,得到最低层次相对于最高层次的综合权重,利用权重求出各方案的优劣排序。其思路是:首先,构建层次结构模型,将船舶操纵性指标因素进行分组,每组作为一个层次,按照最高层、中间层和最低层排列;其次,构建判断矩阵,根据决策者对各层因素的相对重要性给出定量数值;最后,进行层次单排序及其一致性检验[2]。λmax=ni=1(AW)i/(nWi)
CI=λmax-nn-1 式中:W是λmax对应的特征向量;n为判断矩阵A的阶数;CI是一致性指标。
对8艘船的操纵性优劣进行排序,结果见表4。
层次总排序的一致性检验结果为CI=0.056 8,随机一致性指标RI=1.41,检验系数CR=0.040<0.10。因此,层次总排序具有满意的一致性。
由表4可得,層次分析法所得排序结果为船8船2船5船1船7船3船6船4;PCA法从安全角度客观分析4项指标,所得排序结果为船8船6船7船2船5船4船1船3。由此可以看出:仅船8的排序没变,说明船舶尺寸相差很大时,小的船舶操纵性较好;从船2和船6在两种方法中的排序看,层次分析法重点考虑2项指标的评价结果为船2操纵性优于船6操纵性,而PCA法考虑4项指标的评价结果为船6操纵性优于船2操纵性。
4 结束语
船舶操纵性评价是一个多指标系统评价问题,本文运用主成分分析(PCA)法对船舶操纵性进行了综合评价。运用PCA法求解各评价指标的权重,将相关性强的变量转化成彼此不相关的变量,可以减少评价指标间的耦合关系,使得评价过程客观、有效。本方法对样本内的船舶操纵性进行了综合评价,但对于研究不同种类船舶操纵性综合评价规律,还需要选取大量样本做进一步分析。
参考文献:
[1] International Maritime Organization (IMO). Resolution MSC.137(76): standards for ship manoeuvrability[R/OL]. (2002-12-05)[2019-04-16].http://www.imo.org/en/KnowledgeCentre/IndexofIMOResolutions/Maritime-Safety-Committee-(MSC)/Documents/MSC.139(76).pdf.
[2] 洪碧光, 贾传荧. 大型船舶操纵性能综合评价[J]. 交通运输工程学报, 2002, 2(2): 55-58.
[3] 熊云峰, 陈章兰, 袁红莉. 船舶操纵性评价的灰关联分析和逼近理想解法[J]. 中国航海, 2013, 36(3): 86-89.
[4] 张涛, 毕毅. 基于熵权法和模糊集的船舶操纵性综合评价研究[J]. 中国舰船研究, 2013, 8(3): 45-49. DOI: 10.3969/j.issn.1673.3185.2013.03.009.
[5] American Bureau of Shipping (ABS). Guide for vessel maneuverability[S/OL]. [2019-04-16]. https://standards.globalspec.com/std/9896087/145%20CORR.
[6] ABRAMOWSKI T. Application of artificial neural networks to assessment of ship manoeuvrability qualities[J]. Polish Maritime Research, 2008, 15(2): 15-21.
[7] GRNICZ T, KULCZYK J. Application of CFD methods for the assessment of ship manoeuvrability in shallow water[J]. International Journal on Marine Navigation and Safety of Sea Transportation, 2012, 6(1): 57-62.
[8] TRAN K T, OUAHSINE A. Assessment of ship manoeuvrability by using a coupling between a nonlinear transient manoeuvring model and mathematical programming techniques[J]. Journal of Hydrodynamics, Ser. B, 2013, 25(5): 788-804.
[9] WANG Xin, LIU Zhengjiang, CAI Yao. A rating based fuzzy analytic network process (F-ANP) model for evaluation of maneuverability[J]. Ocean Engineering, 2015, 106: 39-46.
[10] 汤旻安, 王攀琦. 兰州市交通拥堵研究[J]. 西北大学学报, 2019, 49(1): 71-77. DOI: 10.16152/j.cnki.xdxbzr.2019-01-009.
[11] 邹云美, 陈军. 21世纪海上丝绸之路我国沿海港口类型化研究[J]. 上海海事大学学报, 2018, 39(3): 64-68. DOI: 10.13340/j.jsmu.2018.03.011.
[12] 洪碧光. 船舶操纵[M]. 大連: 大连海事大学出版社, 2014.
[13] 曹悦恒. 典型国家汽车产业国际竞争力比较研究[D]. 长春: 吉林大学, 2018.
[14] 张建. 船舶操纵性预报及评价[D]. 大连: 大连理工大学, 2008.
[15] 姚杰, 卓永强, 吴兆麟, 等.船舶操纵性综合评价方法的研究[J]. 大连水产学院学报, 2002, 11(1): 42-47.
[16] PERERA L P, MO B. Marine engine operating regions under principal component analysis to evaluate ship performance and navigation behavior[J].IFAC-PapersOnline, 2016, 49(23): 512-517. DOI: 10.1016/j.ifacol.2016.10.487.
(编辑 赵勉)
收稿日期: 2019- 04- 16 修回日期: 2019- 06- 11
基金项目: 国家自然科学基金(51879024);辽宁省自然科学基金(20180520034)
作者简介: 闫成勇(1988—),男,山东菏泽人,硕士研究生,研究方向为交通运输工程,(E-mail)chengyyan@163.com;
章文俊(1977—),男,江苏南通人,教授,博士,研究方向为交通信息工程及控制,(E-mail)wenjunzhang@dlmu.edu.cn

