例谈如何实现数学学习的“深一度”

尹文军

(南京市浦口区行知小学，江苏南京，210000)

深度学习是源于人工智能网络的一个概念，后被教育工作者引入教育教学，一般指在真实复杂的情境中，学生运用所学的知识和技能，对信息进行深度加工，深刻理解和掌握复杂概念的内在含义，并主动建构知识体系，进而以知识迁移推进实际问题解决的学习过程、状态和结果。[1-2]在教学中，为实现学生数学学习的“深一度”，教师需要超越表层的符号教学，[3]对学习材料、学习路径、学习状态做深入细致的思考和探究。

一、研究学习材料的数学本质，实现本质的“深一度”

什么是数学本质？不同角度的分析可能会有不一样的理解。不少学者认为，数学的本质就是探索和研究数学所依赖的那些基本思想，也就是“将具体的数学知识都忘掉以后剩下的东西”，主要包括数学抽象的思想、数学推理的思想和数学建模的思想。最近，也有学者基于数学史的沿革，提出数学本质就藏在数学演变的线索中，那些一直保留的并且不断建构和延展的数学内容，理应就是数学的本质。此话说起来简单，但寻找起来却不是一件容易的事。

要想对“什么是数学的本质”给出一个清晰的、公认的表达，并不是一件容易的事情。问题是一线教师应该怎样凸显相关内容的数学本质，进而有效落实培养学生数学核心素养的改革目标。笔者认为，天下大事必作于细，天下难事必作于易，教师应该从熟悉的教材和课堂入手开展实践和思考。

“认识面积”是小学数学“图形与几何”领域的重要内容。面积的本质是什么？在古代，为了确定农业收成、计算税收，必须丈量土地，由此产生了面积的概念。中国古代形象地用“幂”或“积”来表示面积。其中，“幂”指遮盖物品的方形布，“积”指积累。因此，面积的本质是“面的积累”。小面积大面，是物体表面的本质属性，非比较出来的大小，而是积累起来的“多少”。更重要的是，“幂”是测量面积的标准，即单位。所以，人类对面积的认识源于测量。

基于对面积本质的认识，教师在设计教学时组织学生进行以下测量活动：(1)用铅笔盒的面测量书本面，说说书本的面里大约有几个铅笔盒的面；(2)用书本的面测量课桌的面，说说一张课桌面里大约有几个书本面；(3)观察并说说黑板的面大约有几个课桌的面；(4)用规定大小的纸片测量一张A4纸的大小。通过多个测量任务，学生运用了不同的标准进行测量，在此过程中感受到面积源于对物体表面的测量，测量面积要有一定的标准，面积的大小是指大面积里含有多少个小面积等本质含义。测量活动促进了学生对数学知识本质的深度认识。

二、适时追问核心问题，实现过程的“深一度”

估算是小学数学教学中的一个重点和难点。在第一学段，《义务教育数学课程标准(2011年版)》将“能结合具体情境，选择适当的单位”作为估算的核心。在人教版三年级“用估算解决实际问题”中有这样一道例题：“每张门票8元，29位同学参观，带250元够不够？92位同学参观，带700元够不够？带800元呢？”在解决此题的过程中，学生会用“30”和“90”分别作为“29位同学”和“92位同学”估算的单位，其估算的结果是可靠的。但是，在解决“800元够不够”的问题时，大多数学生仍然以“90人”为单位进行估算，很少有学生想到用“100人”作估算单位。这种情况下，教师可适时追问两个问题：(1)以“90人”为单位进行估算，其估算结果可靠吗？(2)由“带800元”和“每张门票8元”这两个条件，你还能想到什么？通过追问，教师启发学生可以用“100人”做单位进行估算，学生比较之后发现，其估算结果比以“90人”为单位进行估算更可靠。

三、追求数学知识结构化认识，实现认识的“深一度”

平移是物体运动的一种形式。在苏教版四年级下册“图形的平移”中，教师一般通过数格子的方式让学生体会运动的方向、距离以及图形平移前后的大小、形状及位置关系。在这样的教学中，学生对平移的认识往往是零碎的。为了帮助学生建构结构化的知识体系，教师可以尝试以下学习任务：(1)画，画出金鱼图平移的路线；(2)数，金鱼图向( )平移( )格。该任务具有一定的开放性，学生可以采用不同的方式进行探索、解答，呈现出多种不同的画法和数法，如图1—图3。

图1 生1

图2 生2

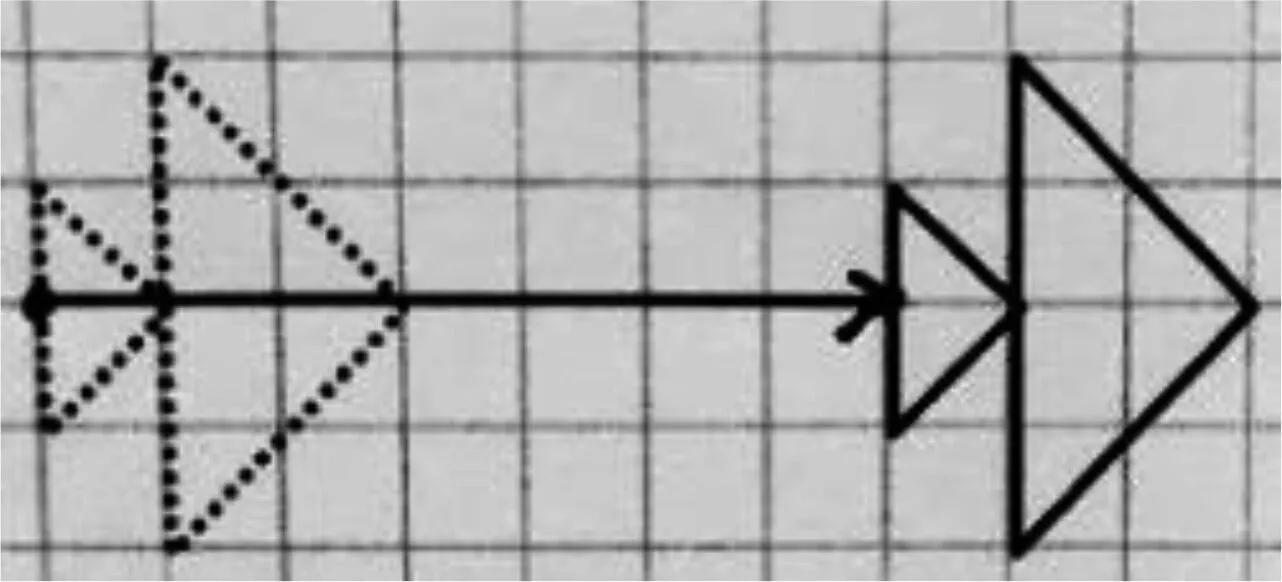
图3 生3

在学生交流平移想法之后，教师可以把学生的几幅平移路线放在同一张图上，帮助学生通过观察、比较、分析，提炼出平移运动的元素和特征，如图4所示。

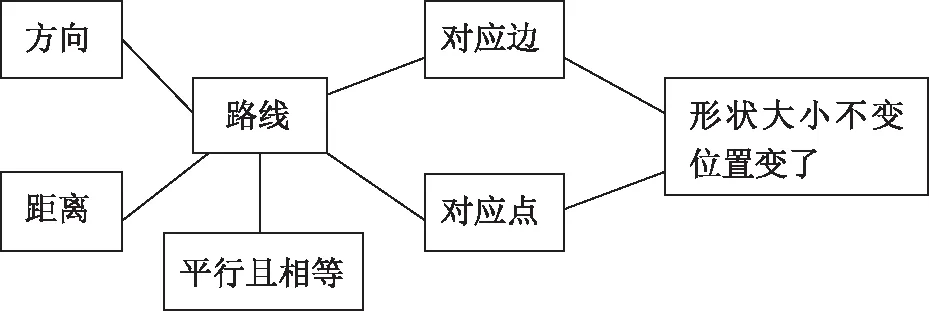
图4 平移运动的元素和特征

从图4可知，以平移的路线为核心，学生动态地认识了平移的本质：一个图形和它经过平移所得的图形中，两组对应点的连线平行且相等。

四、寻求关联、沟通的数学方法，实现方法的“深一度”

数学方法是数学思维的具体体现。由于思维方式和思维能力的差异，在解决具体数学问题时，学生采用的方法也不尽相同。以人教版四年级“鸡兔同笼”问题为例。“笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各有几只？”为了解决这个问题，学生采用了多种方法，其中，比较典型的有画图法、列表法、直接计算法等。

生1：我是画图的，我先画8个头，每个先画两只脚，再一个一个添上两只，边画边数，数到26只，发现鸡有3只，兔有5只。

生2：我是列表的，从鸡有8只，兔有0只开始，一个一个推算出鸡有3只，兔有5只。

生3：我是列式计算的，如果都是鸡，就有8×2=16只，……

图5 解题思路

当学生汇报完各自的想法后，教师对这几种想法进行关联和沟通，绘制出如图5的解题思路。通过关联，学生意识到，虽然表达形式不同，但它们的共同点都是先假设这8只全是同一种动物(鸡或兔)，再根据题中条件进行调整。如此，学生对方法的认识得到升华，思维得以进阶。

五、进行有效的容错、化错，实现思维“深一度”

基于小学生的认知特点，在带着问题和任务自主探索的过程中，学生会出现多种既有共性又有个性的结果，也会经常出现错误的结果。对于错误的结果，教师更多的应应是包容和合理利用。苏教版五年级上册“小数乘小数”的计算一课中，学生计算3.8×3.2时出现了下面两种典型错误：

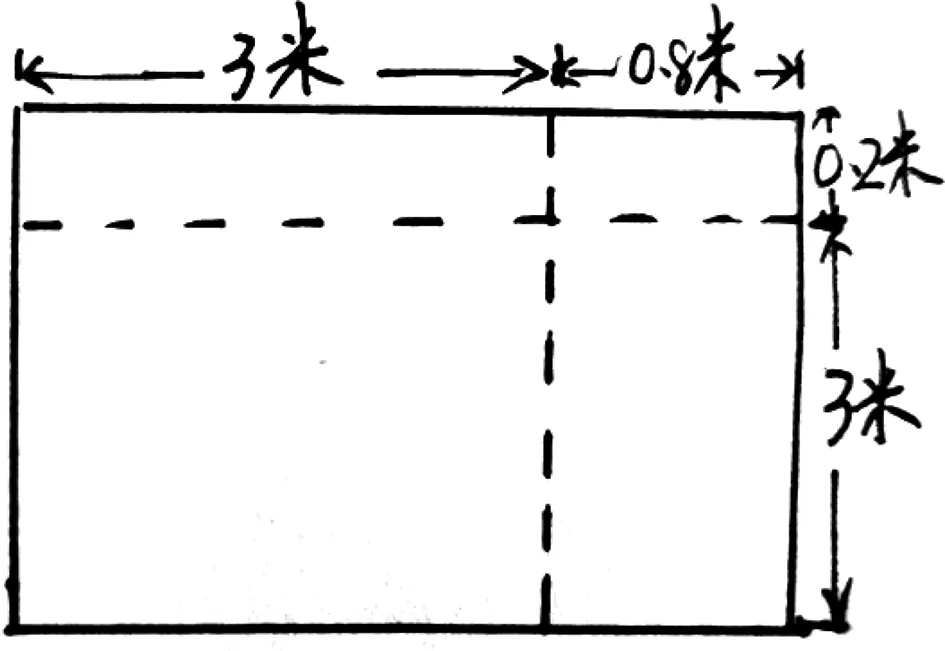
图6 学会绘制的解题图形

错误1：

错误2：

3.8×3.2=9.16(平方米)

此时，教师不必急于判断对错，而是放手让学生尝试用不同的方法画一画、算一算房间的面积。在此过程中，部分学生画出了如图6的图形。“像上面的算法，哪几块面积没有算出来呢？”通过画、质疑、争辩、解释，教师让学生明晰错误，进而真正理解小数乘法的算理。