考虑快慢车模式的地铁地下线纵断面优化研究

孙元广，汪 茜，彭 磊，齐嫣然，柏 赟*

(1.广州地铁设计研究院股份有限公司，广州510699；2.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京100044)

0 引 言

地铁线路纵断面设计主要是指坡段的设计，直接影响线路建设成本和列车运营成本[1].目前，对地铁纵断面方案的优化研究主要分为区间与全线的纵断面优化.前者在固定地铁某区间两端车站水平位置与高程的条件下，对区间的坡段设计进行优化[2-7]；后者是在线路起终点固定后，考虑中间车站高程的变化对全线坡段设计进行优化[8-9].

区间纵断面的优化研究较为成熟.Hoang[2]等结合列车操纵提出6种典型的纵断面设计方案，并设计算法对坡度参数进行寻优.Lafortune[3]等开发了一种交互式地铁线路设计系统，辅助纵断面方案设计以降低列车牵引能耗.Duarte[4]等设计了一种梯度恢复算法，以最小化列车牵引能耗为目标生成地铁站间的最优纵断面线型.余路[6]以降低建设和列车运营成本为目标，利用遗传算法优化地铁区间纵断面方案.白骁[7]构建以列车双方向牵引能耗最小为目标的区间纵断面设计优化模型，采用遗传算法求解.

相较于区间纵断面优化，全线纵断面优化需要考虑中间车站高程变化.Lai[8]等构建了以建设成本、用户成本和运营成本最小为目标的模型，用切平面法优化地铁平纵断面方案和车站高程.Li[9]等采用距离变换算法优化轨道交通平纵断面方案和车站高程.

上述研究均未考虑列车停站方案对地铁纵断面设计的影响.由于快、慢车运行轨迹不同，其节能坡设置也有所区别.因此，有必要对快慢车组合运营线路构建纵断面优化模型，求解使建设成本与列车运营成本最低的纵断面方案.

1 问题描述

地铁地下线一般采用盾构法施工，轨道埋深对于盾构机挖掘成本和处理废土成本的影响极小[10].但地下线每隔一段距离需要设置风井，其建设成本取决于轨道埋深[11]，故风井建设成本为本文优化目标之一.线路纵断面方案对列车运行能耗有较大影响[12]，对于快慢车线路而言，线路上运营多种停站方案的列车，同时考虑所有列车的总能耗并乘以电费单价将其转换为金钱成本，作为本文另一优化目标.

进行纵断面设计时，线路起终点位置(起点车站H1和终点车站HM)和平面信息均为已知，车站数量(M)、风井数量和面积通常也已确定.本文通过调整中间站高程(站中心轨道高程)和各区间变坡点的数量与位置，使建设与运营成本之和最小.纵断面方案如图1所示，中间站高程用表示，m表示车站序号；各区间变坡点的水平位置与高程以坐标形式给出，即其中，j表示区间的序号，k表示变坡点的序号，K表示该区间的变坡点的总数量.

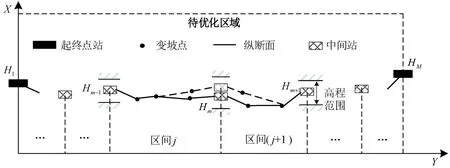
图1 线路纵断面示意图Fig.1 Schematic diagram of track vertical alignment

纵断面设计需考虑的约束主要有两类：第一类是《地铁设计规范》(GB50157-2013)[13]中明确要求的最大纵坡、最小坡长、最小夹直线长度等；第二类为中间站及区间某些地段的控制高程约束，如避让地质不良或管道经过区域，最小埋深约束.列车运行需考虑限速和停站约束等.

综上所述，针对快慢车模式地铁地下线提出纵断面优化模型，在已知线路起终点三维位置和平面方案的条件下，考虑设计规范约束和施工条件，通过改变区间各变坡点的位置和中间站高程，得到以风井建设成本和所有列车能耗成本总和最小的纵断面方案.

2 模型构建

本文考虑最为常见情景，做出如下假设：

(1)线路平面方案在纵断面设计之前已确定，中间站与风井的数量和水平位置，以及风井面积作为已知参数.

(2)列车采用“牵引—巡航—制动”的操纵策略运行，巡航速度等于允许速度减去设定的速度裕量；列车若在运行途中遇到低限速区段，将采用“牵引—巡航—(制动—巡航—牵引—巡航)—制动”的操纵策略，其中，括号内的工况序列出现次数决定于低限速区段的数量.

(3)因再生制动能的利用受时刻表等多方面因素影响，能耗计算不考虑再生制动.

2.1 优化目标

模型目标CO[(X,Y),H]是风井建设成本CF[(X,Y),H]和列车运行能耗成本CE[(X,Y),H]之和最小.风井建设成本属于一次性投入，而列车运行能耗则随时间增加而增大.本文用资本回收系数Δ将风井总建设成本转化为单位年的建设成本[9]，再与年能耗成本相加，得到目标函数，即

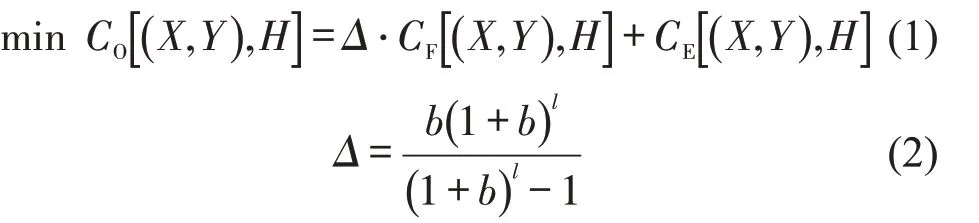
式中：b为年利率(%)；l为地铁生命周期(年).

风井建设成本与其数量、建设面积与埋深有关，前两者为已知参量，风井建设成本主要取决于其埋深，即地面高程与风井高程之差.风井高程等于同里程的轨道高程，地面高程可通过勘察得到.风井成本计算公式为

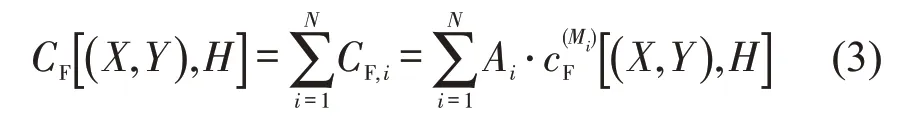
式中：i为风井的序号；为第i个风井的建设单价(万元/m2)，取决于其埋深Mi；Ai为风井i的面积(m2)；N为风井数量.

能耗成本等于所有列车双方向运行能耗之和乘以单价，即

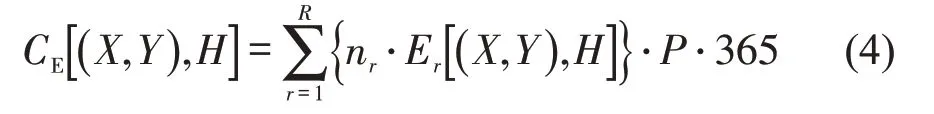
式中：R为列车停站方案数量；nr为1 d 内停站方案为r的运行列次；为停站方案为r的列车双方向运行能耗(kw·h)；P为地铁电费单价(元/kw·h).

列车运行过程中可能受牵引力F、阻力W和制动力B作用，三者均取决于列车速度.计算得到t时刻的列车合力Ct后，根据牛顿第二定律可计算列车加速度at、速度vt、位置St和能耗Et[12]，计算公式为

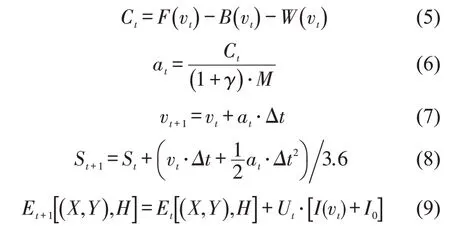
式中：γ表示旋转质量系数；Δt为时间步长(min)；vt和vt+1分别为第t和t+1时刻的列车速度(km/h)；St为列车在t时刻的位置(m)；Ut表示t时刻的瞬时网压；I(vt)表示速度为vt时列车的牵引电流；I0表示辅助设备电流.

2.2 约束条件

(1)《地铁设计规范》约束.

①车站坡的坡度和坡长.

车站区域坡道的坡度值应服从设计规范要求从集合NS中选取，车站区域坡道坡长不应小于站台长度LS[13]，即

式中：NS表示坡度集合，为{-3‰,-2‰,0‰,2‰,3‰}.

②非车站区域坡道的坡度和坡长.

任意坡道的坡长不宜小于远期列车长度LT，坡度的绝对值不小于且不大于，即

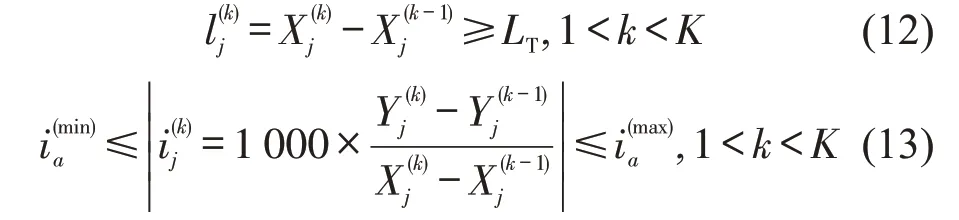
式中：和分别表示《地铁设计规范》(GB50157-2013)规定的非车站区域坡道的坡度值绝对值的最小值与最大值.

③最小夹直线长度.

当相邻坡道坡度差超过2‰时，需设置竖曲线来减缓列车运行时的振动幅度.为避免振动叠加，两竖曲线间的夹直线长度不小于夹直线长度等于相邻变坡点之间横坐标之差再减去两端竖曲线的切线长Tq(Tq取决于相邻坡道的坡度差和竖曲线半径Rc，计算方法可查阅文献[14])，即

(2)控制高程约束.

①车站高程.

由于施工条件与工程造价限制，车站高程值Hm应在一定范围内，即

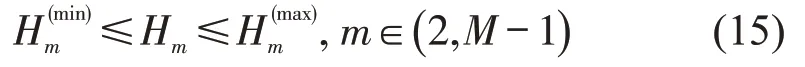
②控制高程.

地下线路施工时通常需避开一些高程区域，如管线经过的区域和地质条件达不到施工要求的区域.因此，在同一里程z下，纵断面经过的高程点与控制高程区域内的任意满足Xh=z控制点h高程值Yh须大于一定的间隔ε，即

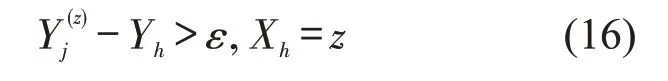
③风井埋深.

考虑施工要求，风井的埋深须大于最小埋深δ，即

(3)列车运行限速约束.

①区间限速.

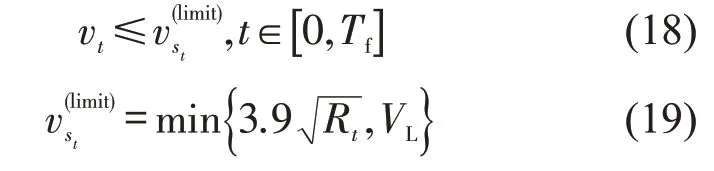
式中：Tf表示列车总的运行时分；Rt表示t时刻列车所处位置处的曲线半径(m).

②车站区域限速.

停站方案为r的列车，其停站和越行站集合分别表示为和.停站时，列车在站中心的速度为0；在越行车站，列车在车站区域的限速为

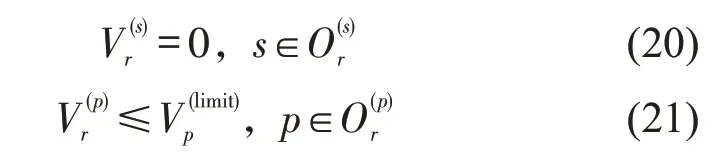
式中：s和p表示车站的序号；表示停站方案为r的列车在车站s的速度；表示停站方案为r的列车在车站p的速度.

3 求解算法

本文模型约束条件多且解空间较大，设计一种双层启发式算法进行求解，上层采用模拟退火算法求解车站高程方案，下层运用遗传算法对区间变坡点的位置进行优化，具体流程如下.

Step 1设置模拟退火算法参数，如初始温度T0，冷却系数ρ，结束温度TN.

Step 2针对中间车站高程，考虑约束条件随机生成一组初始方案，即H0=

Step 3求解给定中间站高程下各区间最优变坡点方案，并计算综合成本C，过程如下：

①设定遗传算法种群大小PM，进化代数G，交叉概率Pc，变异概率Pm.

②通过对各区间变坡点横纵坐标进行间接编码，随机产生个体均满足约束的初始种群.

③计算种群各个体的适应度f，即目标函数值的倒数.

④利用轮盘赌方式选择群体中的两个个体.

⑤对个体进行交叉(两点交叉)与变异(单点变异)操作，生成新个体.

⑥对新个体进行适应度评价.如果优于父代个体，则进入下一代种群；否则，以Boltzmann 准则[15]接受子代.

⑦达到最大迭代次数后，输出当代群体的最优解.

Step 4随机生成一组满足约束的新解H0′，并计算其对应的变坡点方案和综合成本.

Step 5计算相邻两代解的综合成本差值ΔC=C(H0-H0′).若ΔC＞0，则子代被接受的概率为若ΔC＜0，则接受新解.

Step 6更新温度值，Tk+1=ρTk.

Step 7若当前温度Tk达到结束温度TN，输出最优方案；否则，k=k+1，返回Step 4.

4 案例分析

选取广州地铁14号线嘉禾望岗站—新和站区间，长度29.89 km，设有嘉禾望岗、东平、夏良、太和、竹料、钟落潭、黎家塘、新和共8个车站.列车为四动两拖B型车，动车与拖车质量分别为52.5 t和44.5 t，长度120 m.9～15 m、15～21 m、21 m以上的风井单位平方米建设成本分别为2万元、3万元和4万元，其他参数如表1所示.

表1 模型基础参数Table1 Basic parameter of proposed model

为验证模型有效性，本文对比分析实际方案与分别考虑快慢车和站站停得到的优化方案.快慢车模式下：快车仅在嘉禾望岗站和新和站停车，日开行82 对；慢车采用站站停模式，日开行83 对.在站站停模式下，每日开行165 对列车.由于缺少竹料站至新和站的平面方案，为保证可比性，本案例仅优化嘉禾望岗至竹料的纵断面方案.换言之，3种方案在竹料站至新和站采用相同的纵断面.

3种纵断面方案如图2所示.原始方案和两种优化方案的线路长度分别为16 940.000 39，16 940.000 47，16 940.000 51 m.土建成本按7.5万元/延米计算[10]，3种方案施工成本差异可忽略.站站停模式下，纵断面优化方案采用“高站位、低区间”的节能坡设计，因仅考虑站站停列车，车站两端的加减速坡更加陡峭，为列车出站牵引提供更大动力.考虑快慢车模式的纵断面方案由于考虑了快车能耗，东平和夏良站高程较站站停方案均有小幅下降，使整体纵断面线型更加平缓，兼顾快车节能运行规律.

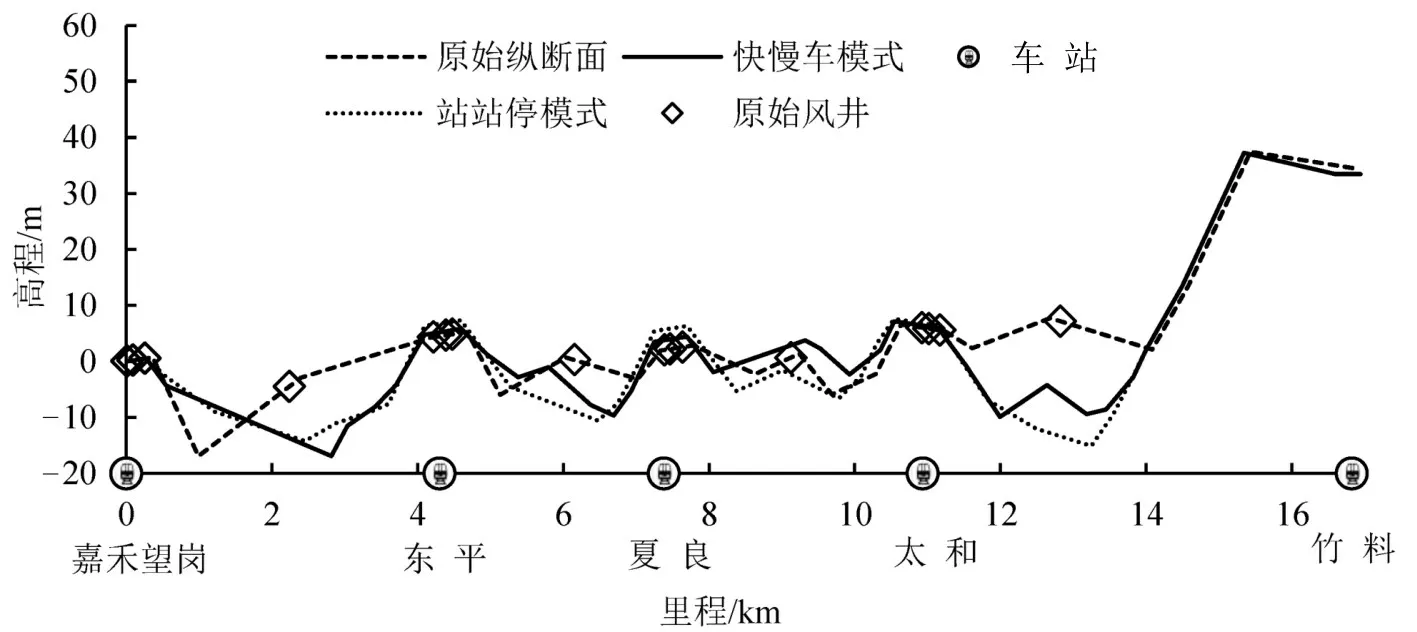
图2 不同方案纵断面对比Fig.2 Comparison on different vertical alignments of subway track

不同纵断面方案的全天双方向列车能耗如表2所示.与原始方案相比，快慢车方案同时考虑快车和慢车的能耗，故快车能耗优化率为2.72%，高于站站停模式的节能率1.52%；而慢车能耗的优化率为2.49%，低于站站停方案的节能率2.53%.快慢车方案的总能耗优化率为2.59%，优于站站停模式的2.10%，说明考虑快慢车停站模式进行纵断面优化的必要性.

不同方案的风井埋深如表3所示.与实际方案相比，快慢车方案中大部分风井埋深均有所减少，故总建设成本降低了36万元.但快慢车方案中的4、8和16 风井埋深均有所上升，且变化幅度与其他风井相比较大.这是由于“高站位、低区间”的纵断面更利于列车节能运行，且能耗成本节约量比埋深增加的风井成本量更大，因此这三处风井的埋深有所增加.此外，由于站站停方案比快慢车方案更注重降低慢车的能耗，使区间纵断面的高程进一步降低，总的风井建设成本较实际方案上升8万元.

表2 不同纵断面方案下的快慢车运行能耗对比Table2 Comparison on energy consumption of train movement with different vertical alignments

表3 不同纵断面方案下的风井埋深Table3 Comparison on ventilation shaft depth with different vertical alignments

不同纵断面方案下的风井与能耗综合成本如表4所示.本文模型的综合成本最小，与原始方案相比总成本降低2.65%，高于站站停方案总成本节省率1.51%.

表4 不同纵断面优化方案下成本对比Table4 Cost comparison with different vertical alignments

5 结 论

本文考虑建设与运营成本，构建考虑快慢车模式的地铁地下线纵断面优化模型，设计求解算法和相应的案例验证其效果，主要结论为：相较于经验丰富工程师设计的纵断面方案，本文模型得到的纵断面方案不仅能减少风井建设成本，同时节约了所有列车的总能耗，可显著降低线路建设与运营的综合成本；与仅考虑站站停模式的纵断面优化方案相比，考虑快慢车模式得到的纵断面方案在节能与减少建设成本方面均表现更好，说明考虑停站模式和建设成本进行纵断面优化的必要性.本文仅研究了地下线的纵断面优化，没有考虑敷设方式变化对线路填挖方成本和路权成本的影响，后续将进一步研究多种敷设方式下的地铁线路纵断面优化问题.