不同湍流模型对风力机叶片翼型气动性能参数计算结果的影响研究

吴友健，杨 艺,2*

(1. 广东海洋大学机械与动力工程学院，湛江 524088； 2. 南方海洋科学与工程广东省实验室，湛江 524088)

0 引言

风力机叶片翼型的气动性能在很大程度上影响着风力机的发电效率[1]。翼型在不同攻角下的气动性能有较大差异，尤其是当翼型处于失速状态时，风力机会产生较大的振动，导致其安全性能降低。因此，准确地预测翼型的气动性能是十分有必要的[2-3]。

由于不同湍流模型对翼型气动性能参数的计算结果会有较大不同，因此选择一种合适的模型来进行数值计算尤为关键[4]，为此，许多学者都进行了相关的研究。丁勤卫等[5]采用S-A、T-SST这2种湍流模型对翼型的气动性能进行了数值计算，结果表明，当翼型出现失速时，T-SST模型可以更好地预测其气动性能参数。彭续云等[6]采用3种湍流模型对NACA63-421翼型进行了气动性能数值计算，结果发现，k-KL-ω模型对阻力系数的预测效果最好；在大攻角范围内，SSTk-ω模型计算得到的升力系数值与实验值最为吻合。

目前对于湍流模型影响翼型气动性能参数计算精度的研究已较为成熟，而将S-A、SSTk-ω和RNGk-ε这3种湍流模型进行综合比较分析的文献较少，甚至大多数文献都未关注到离散格式对翼型绕流数值计算精度的影响。因此，本文选取S-A、SSTk-ω和RNGk-ε这3种湍流模型对风力机叶片NACA0018翼型进行气动性能参数计算，得到一定攻角范围内的气动性能参数情况，然后将其与文献[7]给出的风洞实验值进行对比，并讨论了一阶迎风、二阶迎风、QUICK这3种离散格式对计算精度的影响。

1 翼型的气动性能参数

当来流流过翼型表面时，由于上、下翼面的来流速度不同，导致上翼面的速度大、压力小，下翼面的速度小、压力大。上、下翼面的压差即为翼型所受到的升力，升力沿圆周切线方向的分力推动风轮转动。升力系数Cl、阻力系数Cd、升阻比Cl/Cd均是表示翼型气动性能优劣的参数，其中，升阻比越高，说明翼型的综合气动性能越好。

升力系数Cl的表达式为：

式中，Fl为翼型所受升力；ρ为空气密度；u为来流风速；c为翼型弦长。

阻力系数Cd的表达式为：

式中，Fd为翼型所受阻力。

2 数值模型

2.1 流场数值模型

由于风力机运行时的速度较低，因此，将空气视为不可压缩流体。对于二维定常流动，风力机周围的空气流场的连续性方程为[8]：

式中，x、y分别表示x轴和y轴；ux、uy分别表示x轴和y轴方向上的速度分量。

风力机周围空气流场的Navier-Stokes(N-S)方程为[8]：

式中，v为运动粘度；p为边界层流体压力。

本文采用的3种湍流模型中，S-A模型是一个能够解决湍流粘度的单方程模型，被广泛应用于涉及壁面流动的数值求解中[9]，其输运方程为：

式中，v为湍流运输变量；Gv为湍流粘性产生项；Yv为湍流粘性的破坏项；σv和Cb2为常数项；Sv为自定义源项；ui为流体速度；xj、xi分别为x轴方向上的分量；μ为动力粘度。

SSTk-ω模型是MENTER在k-ω模型的基础上加入k-ε方程得到的。该模型解释了湍流剪切应力的传递，从而可以提高对逆压梯度流的计算精度[10]。该模型的输运方程为[7]：

式中，k为湍动能；t为时间；pk为生成项；ω为比耗散率；μi为湍流粘度；β为封闭系数；σk为常数项。

式中，Gl为混合函数；p∞为无穷远处空气压强；σ∞、σ∞2均为常数项。

RNGk-ε模型是从N-S方程推导出来的湍流模型，形式上与Standardk-ε模型相近，但由于该模型对应变流的计算精度更高，从而扩大了其适用范围[11]，该模型的输运方程如式(9)、式(10)所示：

式中，αk为k方程的普朗特数；μeff为湍流动力粘度；Gb为浮力产生的湍流动能；Gk为速度梯度产生的湍流动能；ε为湍流耗散率；YM为可压缩流体中基于体积膨胀脉动量的耗散率；Sk为其他源项。

式中，αε为ε方程的普朗特数；Sε为其他源项；C1ε、C2ε、C3ε均为常数；Rε为附加项。

2.2 数值求解

采用结构化网格对计算域进行网格划分，网格总数目为36114。由于翼型近壁面区的流动较为复杂，故对近壁面区域网格进行加密处理，图1为翼型近壁面网格分布图。计算域的速度入口设置为10 m/s、压力出口设置为0 Pa、壁面边界设置为绝热无滑移壁面；模拟工况的雷诺数Re为0.82×106；分别建立S-A、SSTk-ω和RNGk-ε模型，压力速度耦合采用SIMPLE算法。由于边界层中无量纲壁面距离y+＞50，故近壁面模拟选择标准壁面函数。当残差的最大值小于10-5时，认为计算收敛。

图1 翼型近壁面网格分布Fig. 1 Near-wall grid distribution of airfoil

3 结果分析与讨论

3.1 湍流模型对计算精度的影响

采用 S-A、SSTk-ω、RNGk-ε3 种湍流模型及二阶迎风离散格式对NACA0018翼型进行数值计算，并将得到的气动性能参数与文献[7]给出的风洞实验值进行比较。该风洞实验的条件为：Re=0.82×106，攻角范围为 2°～18°。

图2和图3分别为不同湍流模型计算得到的升力、阻力系数随攻角变化的曲线图。由图2、图3可知，虽然3种湍流模型计算得到的升力和阻力系数曲线整体走势与实验值曲线相同，但根据文献[7]给出的风洞实验数据，翼型在攻角为14°时进入失速状态，而RNGk-ε模型模拟得到的是翼型在攻角为16°时进入失速状态，因此其对于失速后的模拟不准确，这是因为该湍流模型对于边界层分离现象预测得太迟[12]。

由图2可知，当攻角小于14°时，RNGk-ε模型计算得到的升力系数值与实验值最为接近；当攻角大于等于14°时，S-A模型得到的升力系数值与实验值最为吻合。由图3可知，当攻角小于14°时，RNGk-ε模型计算得到的阻力系数值与实验值较为接近；当攻角大于等于14°时，SSTk-ε模型计算得到的阻力系数值与实验值最为接近，准确度令人满意。

图2 升力系数随攻角变化的情况Fig. 2 Lift coefficient varies with angle of attack

图3 阻力系数随攻角变化的情况Fig. 3 Drag coefficient varies with angle of attack

图4为S-A模型计算得到的翼型在攻角为6°和14°时的流场速度分布图。

由图4可知，当攻角为6°时，翼型后部几乎未出现气流分离现象；当攻角为14°时，翼型后部出现严重的边界层分离，气流不再依附翼型表面流动，这会导致翼型的升力系数下降、阻力系数上升，使翼型进入失速状态。

图4 攻角为6°和14°时的流场速度分布图Fig. 4 Velocity distribution diagram of flow field with angle of attack 6° and 14°

由S-A和SSTk-ω模型模拟得到，当攻角为14°时，翼型进入失速状态，而由RNGk-ε模型模拟得到的失速攻角为16°。当攻角为14°时，S-A和SSTk-ω模型模拟得到的升力系数分别为0.99、0.90，与文献[7]给出的风洞实验值1.05相比，S-A模型模拟的精度更佳；而且该攻角时，S-A模型模拟的阻力系数值与风洞实验值也最为接近。因此在模拟失速情况下翼型的气动性能参数时，S-A模型优于另外2种模型。

3.2 离散格式对计算精度的影响

图5为风速为10 m/s、Re为0.82×106时，采用S-A模型及不同离散格式得到的攻角范围为2°～18°时翼型的升力系数随攻角变化的曲线图。

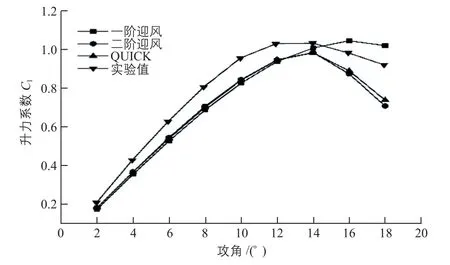
图5 S-A模型下，不同离散格式得到的升力系数随攻角变化的情况Fig. 5 Lift coefficient varies with angle of attack for different discrete schemes in S-A model

由图5可知，当攻角小于14°时，3种离散格式得到的升力系数值与实验值均有一定的差异，但曲线整体走势与实验值曲线基本相同；而且二阶迎风与QUICK离散格式计算得到的失速攻角均为14°，这与实验值一致，但一阶迎风预测的失速攻角为16°。因此，采用二阶迎风和QUICK离散格式进行数值计算更能准确模拟翼型的失速攻角。

图6为风速为10 m/s、Re为0.82×106时，采用S-A模型及不同离散格式得到的攻角范围为2°～18°时翼型的阻力系数随攻角变化的曲线图。

图6 S-A模型下，不同离散格式得到的阻力系数随攻角变化的情况Fig. 6 Drag coefficient varies with angle of attack for different discrete schemes in S-A model

由图6可知，在2°～14°攻角范围内，一阶迎风离散格式得到的计算结果与实验值差异较大，二阶迎风与QUICK离散格式得到的计算结果与实验值较为接近。这是因为一阶迎风离散格式虽然计算速度快，但计算精度低，因此不适用于计算翼型的阻力系数；同时，一阶迎风离散格式对涉及边界层流动的计算会出现假扩散现象，会极大影响计算阻力系数的精度[12]。由此可知，在对翼型进行阻力系数计算时，采用二阶迎风和QUICK离散格式更合适。

4 结论

本文以NACA0018翼型为研究对象，采用S-A、SSTk-ω和RNGk-ε这3种湍流模型对翼型的气动性能参数进行计算，并将计算结果与风洞实验值进行对比，最后分别讨论了一阶迎风、二阶迎风和QUICK离散格式对计算结果的影响，得到如下结论：

1)在未失速(攻角小于14°)时，RNGk-ε模型得到的升力系数值与实验值最接近；当攻角大于等于14°且翼型处于失速状态时，S-A模型计算得到的升力系数值与实验值最为接近，而SSTk-ω模型计算得到的阻力系数值与实验值最为接近。

2)在计算翼型的升力、阻力系数时，二阶迎风与QUICK离散格式都能满足计算精度的要求。而一阶迎风格式对涉及边界层流动的计算会出现假扩散现象，影响计算精度，故在计算翼型绕流问题时不适用。