风扰动对机载单站无源定位精度影响分析*

刘文跃,彭世蕤,何 缓,王广学

(空军预警学院, 武汉 430019)

0 引言

提取相位差变化率定位法以其快速高精度的定位特点在机载单站无源定位中得到了广泛应用[1-4]。该定位方法的关键在于获取高精度的相位差变化率参数[5]。然而在实际应用中,受常值风、突风和大气紊流等风扰动影响[6-9],载机在飞行过程中会发生飞行姿态扰动,从而使固定在无人机机身上的干涉仪基线矢量指向发生变化,对相位差变化率的高精度获取产生影响,从而影响定位精度。

在实际应用中,风扰动是不可避免的,因此研究风扰动对机载单站无源定位的影响具有较强的现实意义。基于此,文中建立了风扰动下的无人机运动模型,并分别讨论分析了在常值风、突风、大气紊流3种典型风扰动下,采用经典卡尔曼滤波法提取相位差变化率后的定位精度[10]。对无人机载单站无源定位技术的实际运用具有一定的指导意义。

1 风扰动下的无源定位原理

1.1 相位差变化率定位法的定位精度模型

如图1所示,以地面某固定点为坐标原点建立固定坐标系ogxgygzg,ogxg轴指向正东方向,ogyg轴指向正北方向。XOY为机体坐标系,OX沿机身轴指向机头方向,OY指向右侧机翼,OA构成干涉仪基线。R表示无人机和目标间的径向距离，β表示目标方位角,β′表示干涉仪波达角。对于地面固定目标,当目标与载机距离较远时,可以忽略飞行高度,等效至二维平面。无人机姿态可用欧拉角(偏航角、俯仰角和滚转角)描述。由于在二维平面内不需考虑俯仰角,并且干涉仪位于无人机机身轴上时,无人机发生滚转时不会对相位差及其变化率的测量产生影响,因此无人机姿态只考虑偏航角φ。

图1 风扰动时一维干涉仪定位示意图

从图中可以看出β′=β+φ。根据空间关系和相位差变化率的定位原理可推出[11]:

(1)

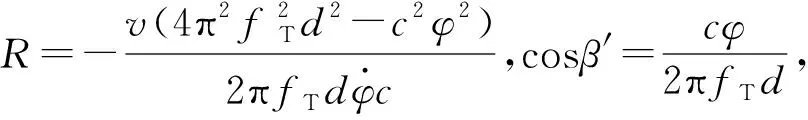
从式(1)可由看出,风扰动带来的姿态变化φ对定位结果直接产生了影响,然而在实际应用中,通常假设无人机做匀速直线运动无姿态变化,即令式(1)中φ=0,此时定位模型变为:

(2)

这显然会引入定位误差:

(3)

式中:δx、δy分别表示x、y方向的定位误差；xT、yT表示无人机真实位置坐标;x′T、y′T表示无人机忽略风扰动带来的姿态变化得到的位置坐标。

定义定位精度δ:

(4)

为了量化分析风扰动对定位精度带来的具体影响,还需要量化风扰动对无人机飞行姿态的影响。

1.2 风扰动下的无人机运动学模型和航迹模型

无人机的六自由度运动学方程为[12]:

(5)

式中:θ、φ、ψ为欧拉角；p、q、r为对应欧拉角角速度;γ、χ为航迹角。以上无人机运动参数的详细定义见文献[12]。va、vk、vw分别表示无风扰动时无人机的飞行速度矢量,有风时无人机的飞行速度矢量和风速矢量,三者有以下矢量关系:

vk=va+vw

通过以上关系就可以将风速作为参量引入无人机运动学模型中。再通过式(5)可以得到风扰动下无人机的实时姿态角,量化了风场对无人机飞行姿态的具体影响。

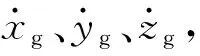
ΔP=vk·Δt

(6)

式中:ΔP表示航迹点采样间隔内的航迹矢量;Δt表示采样间隔。则通过式(6)可以给出无人机的飞行航迹信息。

2 典型风场扰动模型

1)常值风

常值风表现为风的大小和方向为确定值[13],即υw(t)=C,C为某确定常数。

2)大气紊流

大气紊流是指叠加在平均风上的连续随机脉动,平均风是风速的基准值[13]。大气紊流模型一般采用Dryden模型或Von Karman模型,其中Dryden模型的频谱形式简单,是有理式,可以作因式分解,便于紊流场的数值仿真,因此文中选择Dryden模型进行大气紊流的仿真。

仿真的基本原理是将白噪声通过成形滤波器得到符合一定功率谱的有色噪声,其中的关键是确定传递函数G(s)。3个速度分量的传递函数为[14]:

(7)

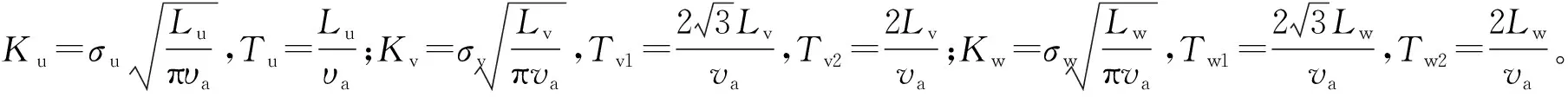
图2 Dryden模型横向紊流片段(Lu=200,σu=1.14 m/s)

3)突风

突风又称阵风,表现为确定性的风速变化,在工程应用中,通常采用1-cos型突风结构,其数学模型为[15]:

(8)

式中:x表示无人机的飞行距离,单位为m;vm代表突风强度,表示突风风速的最大值,单位为m/s;dm代表无人机在突风区飞过的距离。

将不同风扰动模型代入无源定位模型中,就可以量化分析风扰动对机载单站无源定位带来的具体影响。

3 仿真分析

由于只考虑二维平面,因此风扰动情况只考虑无人机横向和纵向两个扰动分量,忽略垂直方向。

3.1 常值风对机载单站无源定位影响的仿真分析

无人机基本仿真参数设置如下:无人机平行大地平面做匀速直线运动,无姿态扰动时飞行速度为150 m/s,无人机初始位置为(0,0),另外在无人机运动学模型中引入传感器自身带来的测量误差,假设在横、纵向速度分量误差满足均值为0、方差为0.5 m/s的高斯分布,并定义风向角η为风速矢量与无人机机头方向的夹角。

风向角η固定为15°,取常值风速大小分别为v=5 m/s,15 m/s,25 m/s时(依据风力等级划分参考表,分别代表微风、疾风、狂风),仿真结果如图3。

图3 风速改变时常值风影响下的偏航角和定位精度

从仿真结果可以看出,在姿态角方面,姿态角抖动程度相当,可以认为常值风的风速大小对无人机姿态角的影响较小。在定位误差方面,可以看出定位误差均在开始阶段有较大幅度波动,而后稳定在一定水平,这是因为在定位过程中采用卡尔曼滤波法提取相位差变化率,由卡尔曼滤波先波动后稳定的特点造成了这样的仿真结果。还可以看出,随着常值风速的变大,定位误差也随之增大,为了更加直观地表达误差,取经过100 s(从图中3可以看出此时定位误差趋于稳定)后的定位精度的均值作为平均定位精度进行分析,单位为km,表达式如下:

(9)

式中:δi表示第i时刻的定位误差,n1取t=100 s时刻对应的采样点数,n2=n1+2 000,即共选取2 000个采样点共计100 s的误差计算定位精度。

则误差数值如表1所示。

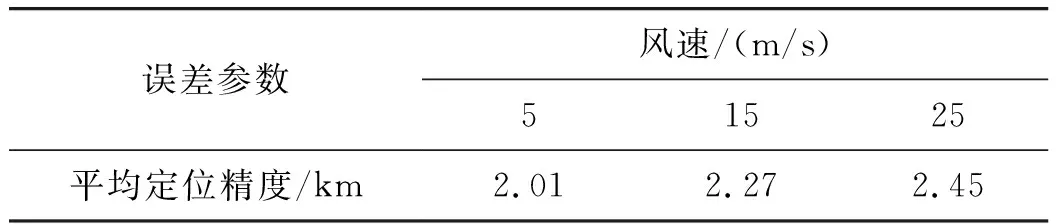
表1 常值风风速影响下误差水平对比

风速大小固定为15 m/s,取常值风风向角分别为η=15°,45°,75°时,仿真结果如图4。

图4 风向改变时常值风影响下的偏航角和定位精度

从上述仿真结果可以看出,常值风的风向角变化对无人机偏航角的影响同样较小,而随着风向角的变大,定位误差也随之加大。这是因为风速可以矢量分解为沿无人机机头方向与沿无人机机翼方向的两个速度分量vwx和vwy,vwx和vwy即为风速带来的速度误差,随着风向角的变大,vwx变小,vwy变大,而且无人机自身在沿机头方向本来就有较大的飞行速度,因此vwx带来的相对误差较小,在仿真条件下速度的相对误差不超过17%,而在机翼方向,无人机的飞行速度在风的影响下风速大小由基本为零变为vwy,即速度误差呈几何倍数增长,机翼方向风速的相对误差很大,因此风向角的变大会使定位误差加大。具体误差如表2示。

表2 常值风风向影响下误差水平对比

综上,风扰动为常值风时,风速的大小和方向均会对无源定位结果产生影响,并且造成影响的主要原因是风速影响了无人机的飞行速度。

3.2 大气紊流对机载单站无源定位影响的仿真分析

在进行仿真分析时,为了更加贴合实际,令无人机横向、纵向和垂直向上均受大气紊流影响,然后取无人机航迹在大地平面的投影以及偏航角代入定位模型进行计算。

根据文献[13],令紊流尺度Lu=2Lv=2Lw=200 m,并假设风具有各向同性,即各个方向的紊流强度相等,令σu=σv=σw=σ,当紊流强度大小分别为σ=1.14 m/s,1.84 m/s,2.54 m/s时,根据仿真得到的对应最大紊流风速均不超过6 m/s,根据文献[13]对紊流强度的等级划分,以上设置的紊流强度均属于“微弱”等级,仿真结果如图5。

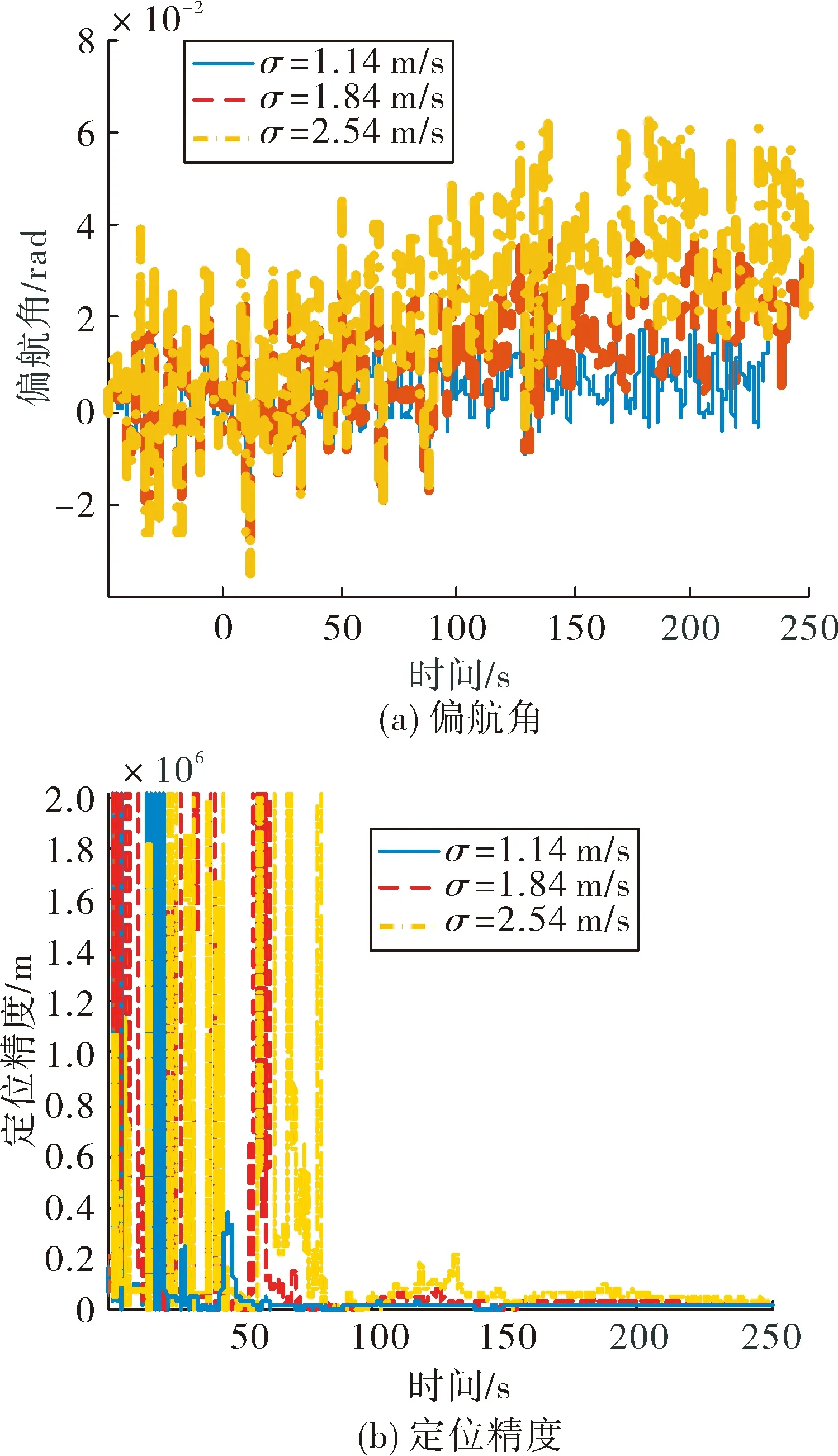
图5 大气紊流影响下的偏航角和定位精度

从仿真结果可以看出,紊流强度变大时,无人机偏航角抖动加剧。从定位误差看,在3种紊流强度下,利用经过卡尔曼滤波提取得到的相位差变化率计算出的定位误差在一定时间后均能收敛到一定误差值,按照式(9)计算平均定位精度如表3所示,但是明显可以看出,紊流强度越大,收敛速度越慢,并且未收敛前的误差越大。

表3 大气紊流影响下误差水平对比

从表中可以看出,用卡尔曼滤波提取相位差变化率的方法在大气紊流强度微弱时仍难以达到理想效果,这是因为卡尔曼滤波在待滤波序列呈线性变化时效果最佳,在无人机做匀速直线运动时相位差线性程度较高,然而风扰动造成的姿态变化导致了相位差的线性程度下降。这也说明了姿态角的抖动会对定位结果产生较大影响。

综上,风扰动为大气紊流时会对无源定位结果产生影响,并且造成影响的主要原因是大气紊流造成了无人机姿态角的抖动。

3.3 突风对机载单站无源定位影响的仿真分析

突风的仿真条件设置如下:突风尺度为dm=200 m,突风开始时刻为100 s,突风风向角为15°,突风强度分别为vm=5 m/s,15 m/s,25 m/s时,仿真结果如图6(只显示风速变化对应时间段内的仿真结果)。

图6 风速改变时突风影响下的偏航角和定位精度

从仿真结果可以看出,突风会对无人机飞行姿态和定位结果造成较大影响,当突风出现时,无人机姿态会产生较大幅度的扰动,并且在突风的影响下,定位误差随突风强度变大而变大,这也说明了采用卡尔曼滤波法提取相位差变化率的方法在无人机受到突风扰动时难以得到较好的定位结果,显然突风导致的姿态变化同样导致了相位差的线性程度下降。同样取100 s(突风开始时刻)后的误差计算误差水平如表4。

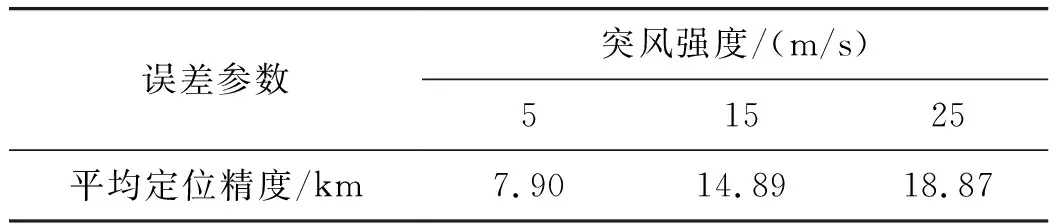
表4 风速改变时突风影响下误差水平对比

当突风强度为vm=15 m/s,突风风向角分别为η=15°，45°,75°时,仿真结果如图7。

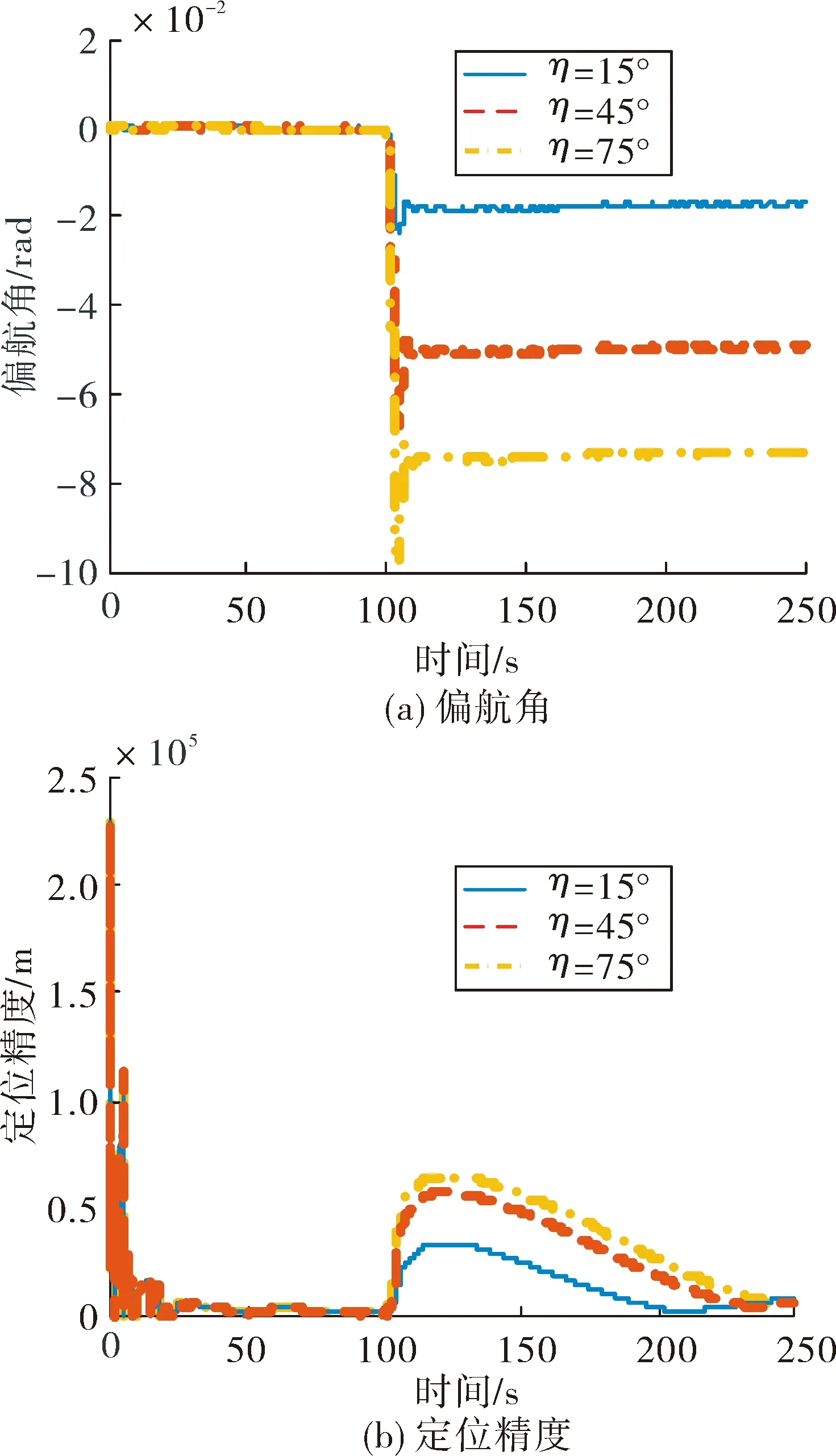
图7 风向改变时突风影响下的偏航角和定位精度

从仿真结果看出,风向角变大,同样对无人机偏航角受到的扰动变大,并且无源定位误差越大,具体误差情况如表5。

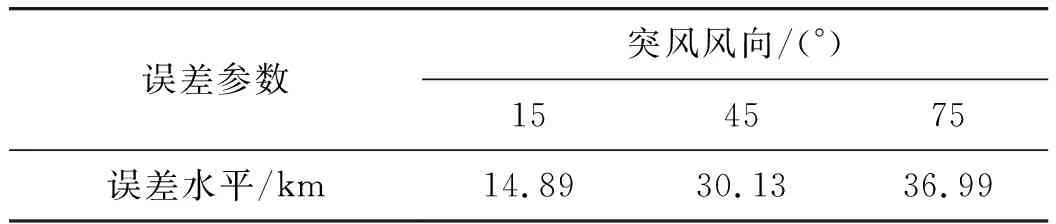
表5 风向改变时突风影响下误差水平对比

综上,突风会使无人机姿态在短时间内发生较大幅度的扰动,并且在突风的影响下,经过卡尔曼滤波提取相位差变化率后的无源定位结果仍存在较大误差。

综合以上3种情况的仿真分析可以得出如下结论:1)当风扰动为常值风时,需要准确估计出无人机在风扰动下的飞行速度才能更加有效地定位;2)当风扰动为突风时,无人机飞行姿态短时间发生较大改变,此时定位误差显著增加,并且由于相位差在风扰动下的非线性程度提高,采用卡尔曼滤波提取相位差变化率的方法难以有效提高定位精度,并且在突风与常值风强度相当时,突风带来的定位误差更大;3)当风扰动为大气紊流时,无人机的飞行姿态角会受到扰动,定位误差显著,采用卡尔曼滤波提取相位差变化率的方法仍难以有效提高精度,并且在紊流强度微弱时的定位误差要大于狂风强度下的常值风与突风带来的定位误差,可以认为大气紊流对定位结果的影响最为显著。综上所述,风扰动对机载单站无源定位的影响不容忽视,需要提出一些新的技术与方法来对这一影响进行补偿。

4 结束语

文中从常值风、大气紊流、突风3种典型风场扰动出发,量化分析了风扰动对测相位差变化率的机载单站无源定位技术的影响,对该定位方法的实际应用具有参考价值。同时得出了风扰动会导致相位差的线性化程度降低,采用经典卡尔曼滤波提取相位差变化率难以有效提高定位精度的结论,因此还需要研究风扰动下的相位差变化率的提取方法来提高风扰动时的定位精度。文中虽然只考虑了二维平面的扰动,但是，其分析方法同样适用于三维定位模型。