BIM技术在新桥大桥拱圈转体施工中的应用

周 权，石峻峰,2

(1 湖北工业大学土木建筑与环境学院，湖北 武汉 430068； 2 中煤三建机电安装工程有限公司，安徽 宿州 234000)

1 工程概况

新桥大桥位于淮南市寿县，路线呈东西走向，是新桥国际产业园西向的出城口道路，设计车速为80 km/h。新桥大桥全长726 m，桥跨布置为：3.0 m(桥台)+10×30 m(预制箱梁)+150 m(斜跨拱)+9×30 m(预制箱梁)+3.0 m(桥台)，其中主桥跨越规划江淮运河河道。主桥道路中心线水平面投影为直线，纵断面的变坡点位于通航净空中心处，两侧分别为2.4%和2.476%的纵坡。

主桥为斜跨钢箱拱桥，主梁跨径为150 m；钢箱拱跨径170 m，矢跨比为0.3819，拱肋轴线与桥梁纵向水平面夹角为25°，拱肋高达68 m。主梁法线方向与规划江淮运河中心线夹角为18.69°。全桥共设12对吊索，使拱肋与桥面连接形成稳定体系[1]。

2 门式桅杆设计说明

根据新桥大桥周围地理环境、现场实际情况、施工成本及施工技术水平，新桥大桥拱肋的施工方案采取工厂分节段拼装，然后运至现场完成拱肋整体拼装。拱肋的现场施工顺序为：拱肋左右端水平拼装、门式桅杆竖立、滑轮组穿绳、通过牵引稳车完成左右两端拱肋转体到预定位置、中段拱肋现场组装并竖向提升至理论位置、下放两端拱肋到理论位置并完成拱肋合拢施工。

门式桅杆底部通过铰链与地面连接，桅杆整体的固定工作由桅杆顶部的揽风绳连接地面来完成。

2.1 验算主要内容

按照现场施工过程及前期受力计算书中提出的危险状态，选择边拱起吊和中拱起吊两个状态为最不利工况，对横梁、支座传力箱体、桁架及桅杆整体的位移及强度进行分析。

2.2 门式桅杆布置说明

门式桅杆布置具体如下:

1)桅杆底部0～10 m范围内的钢桁架结构采用变截面设计，所选材质均为Q345。主支撑间距由700 mm×1000 mm变为2200 mm×2700 mm。变截面部分四角主支撑采用300 mm×300 mm×20 mm方管。底部高度0～960 mm范围内方管外围焊接20 mm厚钢板进行加强。960～10000 mm节段变截面部分横向布置间距为：1@1 m，4@2 m；规格为100 mm×100 mm×6 mm方管。变截面部分斜撑规格为100 mm×100 mm×6 mm方管;

2)中间部分等截面桁架由15节标准节段拼装组成，所选材质均为Q345。单节标准节段高度为4 m，主支撑间距为2200 mm×2700 mm。四角主支撑采用300 mm×300 mm×12 mm方管。交叉撑中部横撑采用140 mm×140 mm×6 mm方管。交叉撑及其它横撑采用100 mm×100 mm×6 mm方管;

3)横梁及下部传力箱模型采用Q345和Q420q的板单元构成。门式桅杆如图1所示。

图1 门式桅杆模型

图2 拱圈及支架BIM模型

3 结构计算

采用Tekla作为新桥大桥BIM信息化模型[2]建模软件，依据设计图纸，建立主桥部分BIM模型，模型精度达到LOD300。该等级的模型单元等同于传统施工图和深化施工图层次[3]。此模型已经能很好地用于成本估算以及施工协调包括碰撞检查，施工进度计划以及可视化。BIM模型如图2所示。

3.1 计算模型及边界条件

利用Tekla建立的门式桅杆BIM模型，导出dxf线模，再导入Midas中进行前处理，得到门式桅杆的计算模型，大大减少了建立计算模型所需的时间和不必要的重复工作。计算模型如图3、图4所示。

图3 桅杆整体计算模型

图4 横梁45度侧视图

计算模型的边界条件设置如下：1)桅杆底部在横梁长边方向为铰支；2)横梁底部在横梁短边方向为铰支。

3.2 荷载计算

利用Tekla建立的拱圈模型，得到起吊时边拱和中拱的重量，来确定拱圈提升时门式桅杆所受到的荷载。

3.2.1 边拱起吊状态所受荷载及荷载方向如表1所示。

表1 边拱起吊荷载

3.2.2 中拱起吊状态待边拱起吊到位后，开始提升中拱，此时横梁受力最大，且受弯剪扭复杂应力组合，处于最不利状态。所受荷载及荷载方向如表2所示。

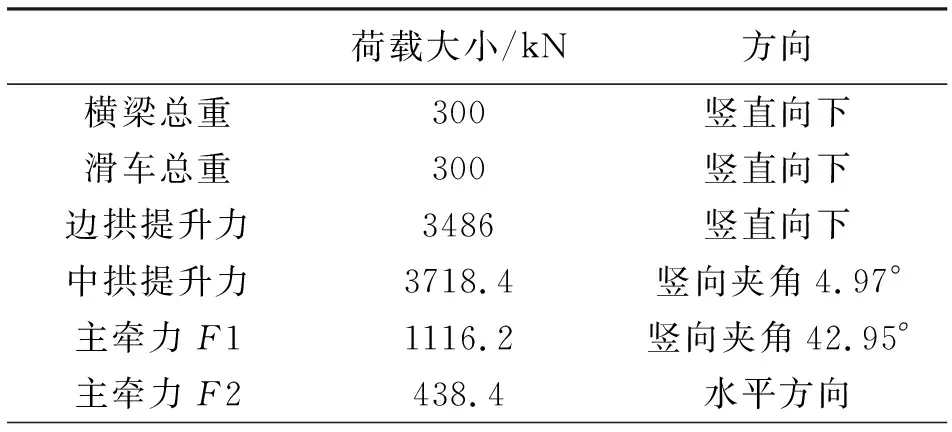
表2 中拱起吊荷载

3.2.3 其他细节说明

1)横梁部分：由于横梁受力复杂，桅杆的重要性极高，故考虑重力荷载外所有荷载乘以2.0，以便达到2.0的安全系数储备。

2)支座下传力箱体：支座下传力箱体位于横梁两端正下方，承受来自于铰链从横梁传递下来的竖向力和水平力。同时，将竖向力和水平力传递到下部桁架。和横梁一起计算，自动考虑横梁传递下来的水平力和竖向力，不再列出。

3)桁架：桁架位于支座下传力箱体正下方，承受来自于支座下传力箱体传递下来的竖向力、水平力及弯矩。与横梁、支座下传力箱体一起计算，自动考虑支座下传力箱体传递下来的所有荷载，此处不再列出。

4)桅杆整体：考虑桅杆整体变形及应力分布情况。整体计算，使用横梁所受外部荷载，此处不再列出。

3.3 结构计算

考虑到该门式桅杆的高度较大，且底部采用铰接释放了Y方向的弯矩，所以桅杆顶部容易产生水平位移。为此，需提前进行桅杆变形及稳定性的计算。通过计算变形得出桅杆在各工况下可能出现的位移，为后期实际施工中利用钢索控制位移提供理论依据和帮助。

1)模型整体变形情况(图5、图6)

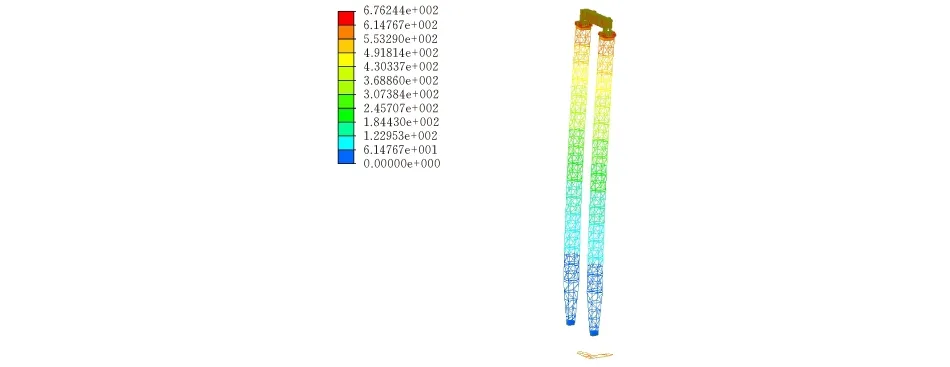
图5 中拱起吊时整体变形情况

图6 边拱起吊时整体变形情况

2)变形结果统计

选取横梁四条边线上的节点为特征点，求得各特征点的位移，以此来统计横梁各部分的位移，横梁边线编号如图7所示。分别计算边拱起吊和中拱起吊两种工况下的位移。

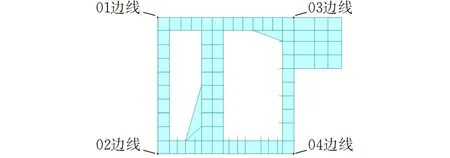
图7 横梁边线编号

选取横梁边线上的控制点，算得其在两种工况下的位移。

位移主要为水平位移，横梁各边线上控制点的X方向位移如图8所示，中拱起吊时X方向最大位移为674.86 mm，边拱起吊时X方向最大位移为-296.04 mm。

图8 横梁控制点X方向位移

特征点Y方向位移如图9所示，中拱起吊时Y方向最大位移为1.02 mm，边拱起吊时Y方向最大位移为1.31 mm。

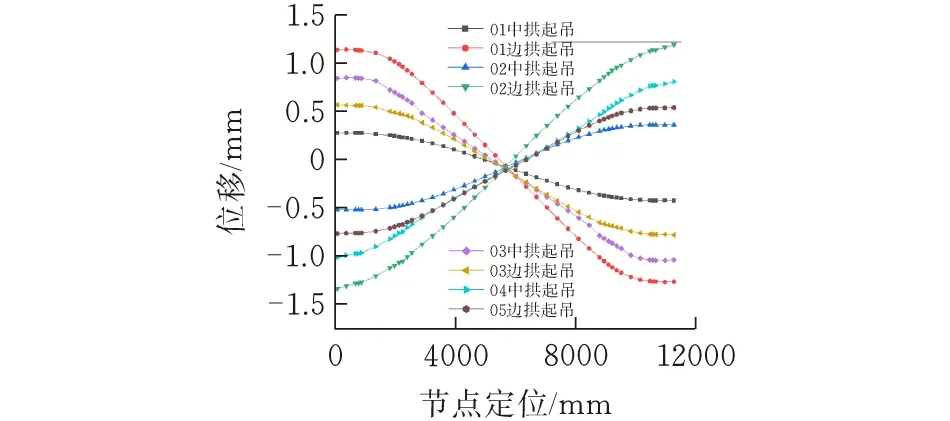
图9 横梁控制点Y方向位移

特征点Z方向位移如图10所示，中拱起吊时Z方向最大位移为-37.74 mm，边拱起吊时Z方向最大位移为-37.09 mm。

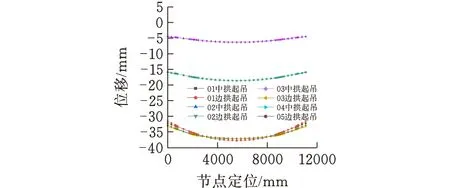
图10 横梁控制点Z方向位移

由于桁架采用底部铰链释放了Y方向的弯矩，在边拱起吊时，横梁扭矩最大，在桁架顶部产生了较大水平位移。在边拱起吊时，最大总位移位于横梁处，为318 mm；在中拱起吊时，最大总位移位于横梁处，为672 mm。

在实际施工过程中，扭矩会传递到桁架上，由桁架承担，缆风可以控制水平位移，控制横梁的水平位置，不会出现计算中出现的水平位移。但计算中较大水平位移提醒我们，由于桁架采用底部铰链释放了Y方向的弯矩，一点很小的不平衡水平力会引起较大的变形，所以要严格控制水平力平衡。

3)应力结果统计

表3 横梁应力分布 MPa

表 4 支座下传力箱体应力分布 MPa

在所有工况下，横梁其余各处的最大等效应力均小于250 MPa，没有屈服区，所以边拱和中拱吊装过程中，横梁的强度符合稳定性的要求[4]。

4 桅杆稳定性分析

4.1 长细比

根据《起重机设计规范》GB/T3811-2008附录J.1，桅杆底部铰支，顶部自由，由于变截面长度较小，且位于底部，做了局部加强，不考虑变截面系数[5]。根据《起重机设计规范》GB/T3811-2008表J-1，长度系数值取2.00。

根据《起重机设计规范》GB/T3811-2008第6.6.1.1条，主要受压承载结构件[λ]=120～150；桅杆桁架为受压的主要承载结构件,长细比λhx=λhy=67<120,长细比满足要求。

4.2 稳定系数

桁架的截面类型对x、y轴均为b类。Q345表示屈服点为345 MPa，抗拉强度约490～620 MPa，σb=490 MPa,σs=345 MPa。根据《起重机设计规范》GB/T3811-2008第6.6.1.1条得假想细长比λF=81.2。

根据《起重机设计规范》GB/T3811-2008附录表K-2,查得b类截面轴心受压构件的稳定系数φ=0.678。

4.3 抗弯模量

4.4 许用应力

4.5 整体稳定性分析

根据《起重机设计规范》GB/T3811-2008 第6.6.3条得压弯构件的整体稳定性。由横梁传递到单边桁架顶部轴心的轴向压力(取中拱加2倍荷载时的轴力，边拱时为14000 kN)和弯矩(取边拱加2倍荷载时的弯矩)分别为：F=8500 kN；My=2550 kN·m；桁架的截面类型对x、y轴均为b类：Mx=0，为单向压弯构件。

5 结束语

1)运用Midas civil对新桥大桥的临时桅杆支架进行了力学验算，通过使用Tekla建立的三维模型，大大减少了有限元软件的建模时间，也避免了重复建模的浪费，对之后的BIM软件在实际工程中的充分利用提供了一定的思路和帮助。

2)通过Midas的结构计算，在考虑了横梁及滑车重力、边拱提升力、中拱提升力、缆风拉力等荷载的情况下，确保支架整体的稳定性及安全性满足规范的要求，保证了整个门式桅杆体系的安全。

3)全桥拱圈的起吊工程于2019年6月全部完成，现场通过缆风对桅杆的水平位移起到了很好的控制，实际工程中变形及位移也均满足工程要求。因此，该案例的分析结果也能为其他临时支护结构的设计提供参考依据。