基于EFDT-HS随机森林算法的货物装载研究
李 伟,杨超宇,孟祥瑞
(安徽理工大学 经济与管理学院,安徽 淮南,232001)
货物装载是物流运输中至关重要的一部分,高效的装载不仅可以降低运输成本还能缩短装箱时间.从物流运输业兴起到现在,已有很多国内外学者利用各种方法研究三维装箱问题.
Gonçalves[1]提出的有偏随机密钥遗传算法,通过利用箱内的空闲空间提高了箱子的利用率;Yang等[2]和Hifi等[3]利用整数线性规划的启发式策略求解三维装箱问题;Jonas等[4]在决策支持系统中应用两级元启发式方法缩短交货时间和减少货物损坏风险;张德富等[5]提出求解三维装箱的混合模拟退火算法,提高了集装箱的利用率;杨广全等[6]基于遗传算法原理,设计启发式遗传算法,实现集装箱装车配载的智能化;那日萨等[7]提出了一种基于“块”和“空间”的启发式搜索算法,在时间效率和体积利用率均有所提高;刘胜等[8]提出了启发式二叉树搜索算法,装箱率有显著提高;朱莹等[9]提出一种结合启发式算法和遗传算法的混合遗传算法;田维等[10]利用整数规划方法对装箱问题进行快速准确求解;张雅舰等[11]提出了一种改进的遗传算法,使得到最优解的概率更大;李俊等[12]基于两阶段分层求解思想设计SWO-HES两阶段算法,并验证了该算法的有效性;廖星等[13]采用自适应权重法改进了粒子群优化算法,大幅加快了计算速度;范霁月等[14]采用一种基于自适应细菌觅食算法提高了集装箱利用率;郑斐峰等[15-18]通过遗传算法与贪婪策略对比得到遗传算法在求解集装箱装载时结果更优;李孙寸等[16]用多元优化算法实现三维装箱问题得到了理想的结果;尚正阳等[17]利用三维的剩余空间最优化算法实现装箱问题的快速求解.
现实生活中,人们的需求各有不同,这就涉及到多规格货物的混合装载问题.为了保证货物的高效运输,本文提出了一种启发式随机森林算法,旨在保证集装箱利用率的同时,缩短集装箱的装载时间.
1 问题描述
多规格货物装载是指将尺寸不一的货物装载到同一集装箱中的过程.为使本文研究目标更直观,我们将目标描述如下:
给定一个集装箱容器C和一系列待装货物的集合B,假设集装箱和待装货物均为长方体.集装箱的长为L,宽为W,高为H,体积V=LWH;每个待装货物bi的长为li,宽为wi,高为hi,体积vi=liwihi.我们的目标是利用集合B生成K个训练集Bi,每个训练集Bi的目标是在Bi中寻找一个子集F,使得集装箱C的空间利用率最大.通过对训练集的求解,可以得到K个集装箱的空间利用率,对K个利用率进行求和平均来得到容器C在集合B情况下的利用率.即
maxfitness=VF/V=∑liwihi/V
{B1,B2,…,Bi}∈B
2 EFDT-HS随机森林算法
本文算法是在随机森林中CART树构造部分融合了极快决策树(Extremely Fast Decision Tree,简称EFDT)和启发式搜索算法(Heuristically Search,简称HS)形成了基于EFDT-HS的随机森林算法,此算法首先利用Bagging方法生成T个训练集,对每个训练集要求在特征集中随机选取K个特征组成新的特征集,将新特征集中的最优特征作为分割特征,利用分割特征计算并择优选取样本信息熵,然后构建生成货物装箱决策树模型,最后基于启发式搜索方法对货物装载后的剩余空间进行合并再利用.
2.1 随机森林算法
随机森林是集成学习下的产物,是将许多棵决策树整合成森林,用来预测最终结果.简单来说,随机森林= Bagging算法 + CART决策树.
2.1.1 Bagging算法
Bagging算法是模型融合的方法,可以将弱分类器融合之后形成一个强分类器,且融合之后的效果会比最好的弱分类器更好.算法过程如下:
Step1.从原始数据集中抽取训练集.每轮从原始数据集中有放回的随机抽取n个训练样本.共进行T轮抽取,得到T个训练集.
Step2.每次使用一个训练集得到一个模型,T个训练集得到T个模型.
2.1.2 融合EFDT的CART决策树
本文在CART树构建时引用极快决策树的择优思想,在集装箱装载时,把每个数据集的装载看做一棵树的形成,把每个要放入的箱子看做一个叶节点,在满足条件约束的情况下,选择对应分割特征信息熵最大的箱子装入.
1)最优特征选择方法
线性回归损失函数是以最小化离差平方和的形式给出的,回归树使用的度量标准也是一样的,通过最小化残差平方和作为判断标准,公式如下:
Yi为样本目标变量的真实值,R1,R2为被划分的两个子集,C1,C2为R1,R2子集的样本均值,j为当前的样本特征,s为划分点.
2)极快决策树节点选择
极快决策树是HATT(Hoeffding AnyTime Tree)的系统实现[19].HATT使用Hoeffding不等式来确定在最佳属性上进行拆分的优点是否超过没有拆分的优点,或者当前拆分属性的优点.在实践中,如果一个节点上不存在分裂属性,那么当最优候选属性的性能超过次优候选属性时,HATT将在最优候选属性带来的信息增益为非零且具有所需的置信度时进行拆分,而不是只在最优候选属性的性能优于次优候选属性时进行拆分.且当当前最优属性和当前拆分属性之间的信息增益差异非零时,HATT将进行分割,并假设这比没有分割要好.
总而言之,EFDT是通过计算样本数据中每个样本的信息值,在满足Hoeffding不等式的前提下选择相对上一节点信息增益不为零且在样本中信息增益最大的节点为叶节点,即择优选取.
2.2 启发式算法
本文在利用多种货物相互组合使空间利用达到最优思想的同时,考虑到放入的货物的宽度和高度会小于上一装载的货物,于是在货物装箱过程中考虑了“空间合并”和“装载空间再利用”的启发式算法.
2.2.1 空间合并
上文提到要将每一层的装载看作一棵树的形成,在每一层的装载中都可能会有剩余的长度,为了充分利用每一层的剩余长度,本文采用了上下剩余空间合并的方法.
如图1所示,上下空间合并分为三种情况:
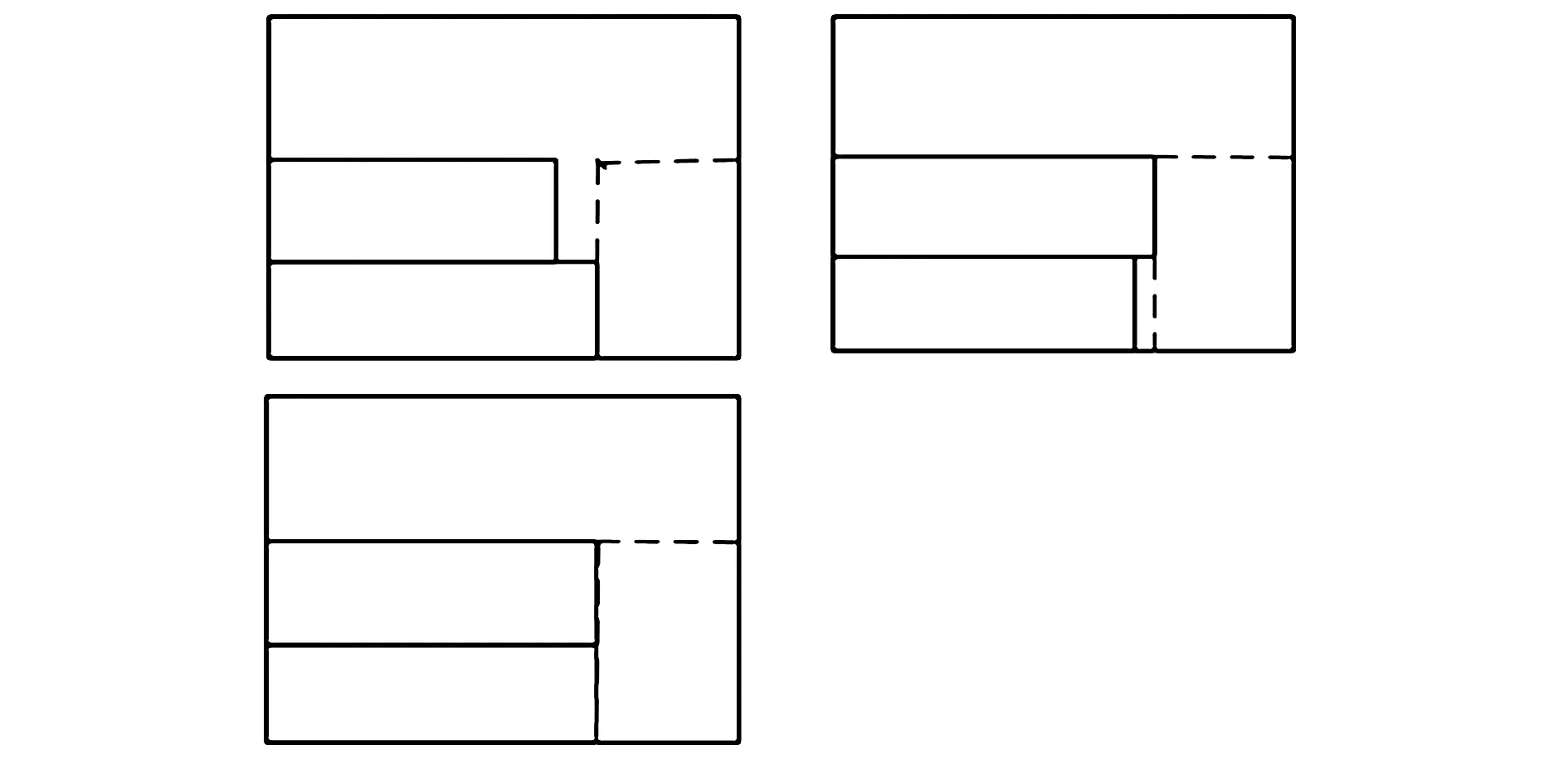
图1 上下空间合并
1)当前装载层的剩余长度大于上一装载层的剩余长度,即图1第一个图.在这种情况下,我们以较短的上一装载层的剩余长度为剩余空间的最大长度,以这一装载列最底层根节点的宽度为最大宽度,以要合并的两层装载空间根节点的高度之和为最大高度.
2)当前装载层的剩余高度小于等于上一装载层的剩余长度,即图1第二个、第三个图.在这种情况下,我们以较短的当前装载的剩余长度为剩余空间的最大长度,以这一装载列最底层根节点的宽度为最大宽度,以要合并的两层装载空间根节点的高度之和为最大高度.
2.2.2 装载空间再利用
由于是多规格货物装载,很有可能出现上一个装载货物要比下一个装载货物宽或者高,于是本文提出了装载空间再利用的想法,目的是尽可能的把空闲空间利用起来.
如图2所示,装载空间再利用分为两种情况:
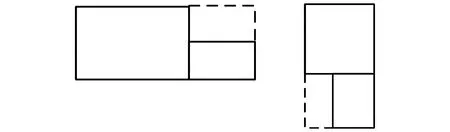
图2 上部剩余空间利用、平行剩余空间利用
1)当前装入的货物高度小于上一装载货物的高度,即图2左图所示,在这种情况下,我们以当前放入货物的长度为最大长度,以当前装载层根节点的宽度为最大宽度,以当前装载层根节点与当前放入货物的高度差作为待利用空间的最大高度.
2)当前装入的货物宽度小于上一装载货物的宽度,即图2右图所示,在这种情况下,以当前装载层根节点与当前装入的货物的宽度差作为最大宽度,以当前装入货物的长度作为最大长度,以当前装载层根节点的高度作为最大高度.
2.3 EFDT-HS随机森林算法在多规格货物装载中的应用
将集装箱看做三维坐标系,假设x轴为集装箱的长,y轴为集装箱的宽,z轴为集装箱的高,从集装箱最里面靠左开始装载,先沿x-z面进行装载,x-z面装载完成后再沿y轴增加一列继续沿x-z面进行装载.每个装载函数的决策树节点选取时都选择划分特征对应信息增益最大的货物.以底层装载函数为例.
2.3.1 底层装载函数
底层装载,即此时装载层的长度占用为0,高度占用也为0的情况,反映到坐标系中即为X=0,Z=0的情况.底层装载函数步骤如下:
Step 1.初始装箱,选取待装货物中最优特征值最大的货物作为装入的第一个货物,作为根节点.读取此货物的长宽高,计算当前装载层的剩余长度、最大宽度、最大高度、剩余宽度.
Step 2.在剩余待装货物中取出符合剩余长度、最大宽度、最大高度的箱子,计算这些箱子的最优特征值,并按照箱子编号和对应最优特征值降序排列.取最优特征值最大的箱子装入.在装入每层非第一个箱子后,都判断装入箱子的上部空余空间和平行剩余空间是否还能放入箱子.(箱子可旋转)
Step 3.更新此装载层的剩余长度,重复步骤Step2,直到没有满足的箱子.
Step 4.返回装箱结果、待装货物、此装载层的最大宽度、剩余空间的长度、集装箱剩余高度、集装箱的剩余宽度.
2.3.2 算法的综合应用
Step 1.读取待装货物数据,将其转化为要求的格式.
Step 2.利用Bagging方法在原始数据中有放回的随机抽取组数据集,每组个数与原始数据个数相同.
Step 3.读取特征集D,将其转化为要求的格式.
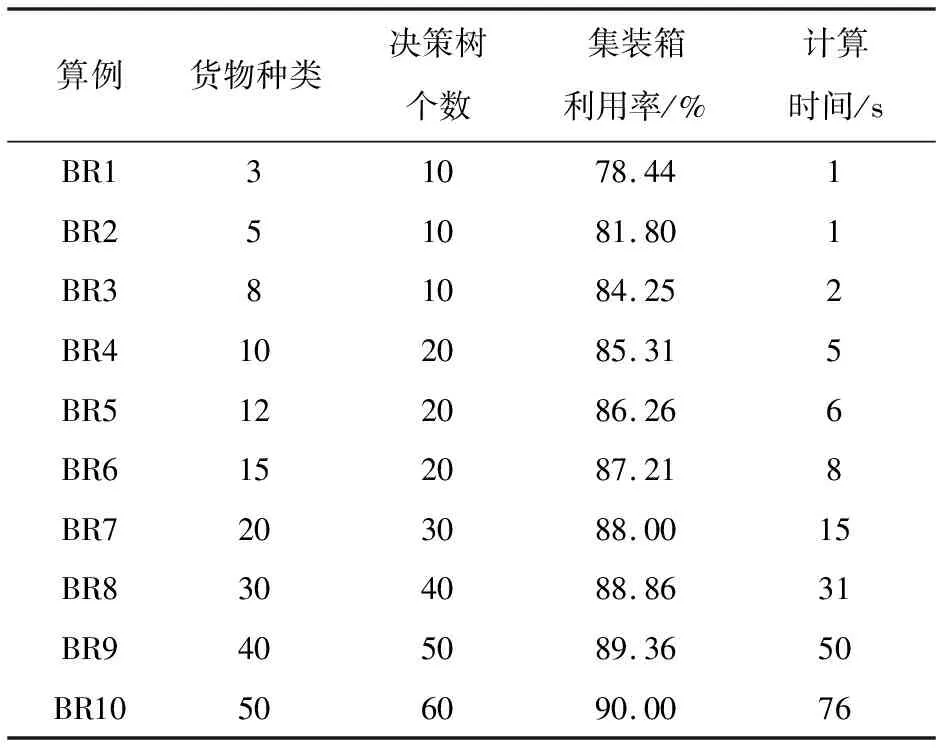
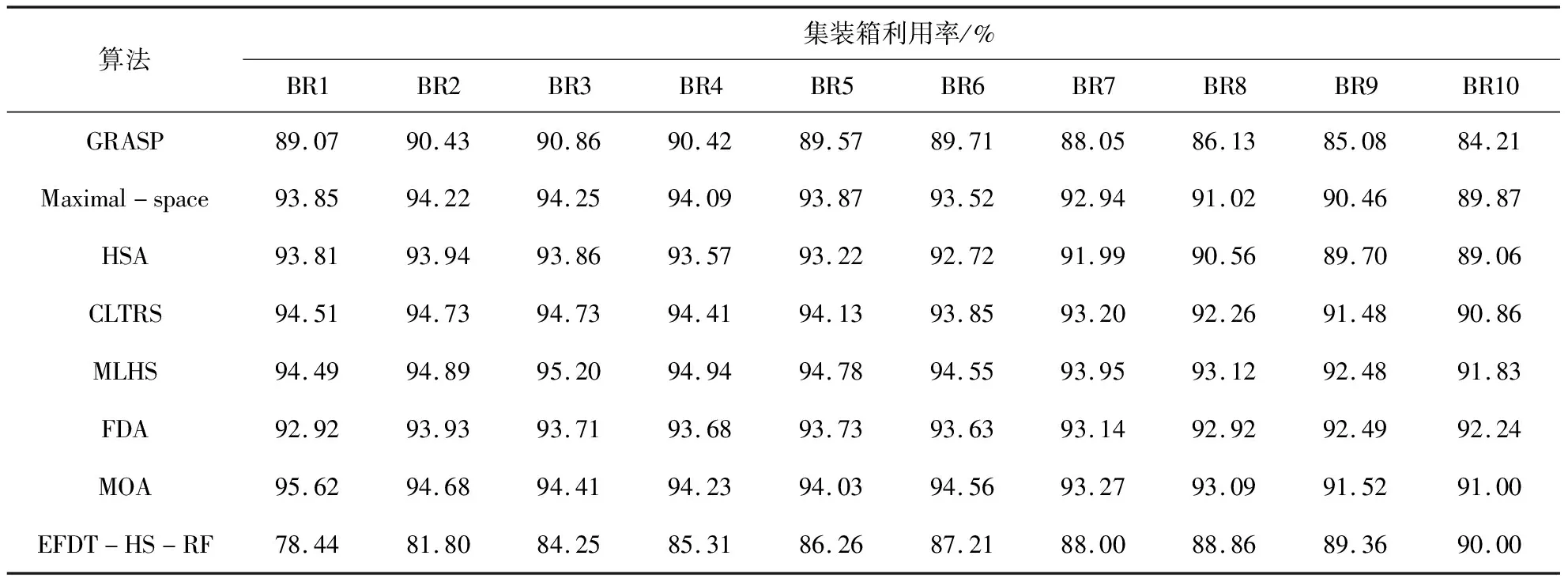
Step 4.读取Step 2生成的数据集Ti,i=1,2,…,T,并在步骤Step 3读取的特征集中随机不重复的选取K个特征,K Step 5.对于数据集Ti根据最优特征选择相应的装载方法,形成一棵决策树Mi. Step 6.重复Step 4、Step 5T次,得到T棵决策树.聚合这T棵决策树,得到预测结果: 本文基于Python程序实现了该算法,为验证本文提出方法的有效性,采取OR-Library[20]中BR1~BR10十个算例数据进行测试,十个算例中每个算例包含100个子算例且每个子算例箱子种类数分别为3、5、8、10、12、15、20、30、40、50,异构性从弱到强,实例计算中所用集装箱为国际标准集装箱,尺寸为587 cm×233 cm×220 cm.通过Python程序分别对十组算例进行计算,算例结果如表1所示. 由表1可知,随着货物异构性不断增强,集装箱的空间利用率不断增加,同时,随着决策树个数的增加,算法的计算时间也在缓慢增长. 表1 BR1~BR10计算结果 对于BR1~BR10这1 000个算例,许多国内外学者对其进行过测试,本文对文献[21]提出的贪心随机自适应搜索算法(GRASP)、文献[22]提出的贪心随机自适应搜索算法(Maximal-space)、文献[5]提出的禁忌搜索算法(HSA)、文献[23]提出的贪心随机自适应搜索算法(CLTRS)、文献[24]提出的提出的多层启发式搜索算法(MLHS)、文献[25]提出的FDA算法、文献[16]提出的多元优化算法(MOA)等比较经典的算法得到的装箱结果进行比较分析,集装箱利用率比较结果如表2所示. 表2 各种算法的集装箱利用率比较 各算法集装箱利用率对比图如图3所示. 图3 各算法集装箱利用率比较 从图3和表2可知,各算法随着货物种类的增加,集装箱的利用率呈下降趋势,而本文算法的集装箱利用率成上升趋势,且一直保持较高状态,由此可见,本文算法在求解多规格货物装载中具有一定优势. 时间对比图如图4所示. 各种算法的计算时间对比如表3所示. 由图4和表3可知,随着待装货物种类的增加,各算法的计算时间大幅度增加,而本文算法的计算时间呈缓慢增长趋势,在各算法的计算时间中一直保持最低状态.由此可见,该算法可以有效缩短计算时间,进而减少货物的装载时间,减少时间成本. 图4 各算法计算时间对比 表3 各算法的计算时间结果比较 随着装箱问题的深入研究,集装箱的利用率不断升高,算法的计算时间也不断延长,如何在保证较高集装箱利用率同时,缩短计算时间受到大家越来越多的关注.本文通过改进随机森林算法中CART树的构造方法,将极快决策树思想融合进CART树中.在决策树的构造过程中保证每个节点划分特征对应的信息增益值最大,在每个货物装载后利用启发式搜索算法对剩余空间进行再利用,有效解决了空间浪费的问题.利用随机森林算法集合多棵不同装载方法下的决策树,更能保证集装箱利用率的准确性.通过对算例BR1~BR10的计算比较,虽然本文算法在弱异构货物中的集装箱利用率不占优势,但在强异构货物装载过程中,相较于MOA算法,BR10的集装箱利用率为91%只比本文算法高出1%,而本文算法却将其平均求解时间由1 380.62 s降低到76 s. 从实际情况来看,人们的需求不断增多,需要运输的货物种类也在不增加,本文提出的启发式随机森林算法主要针对多规格强异构货物的装载,符合现实生活的发展趋势.3 实例计算与结果分析
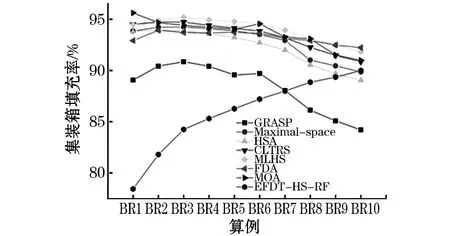
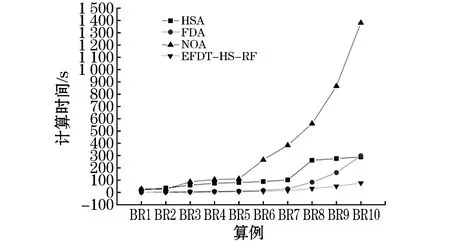
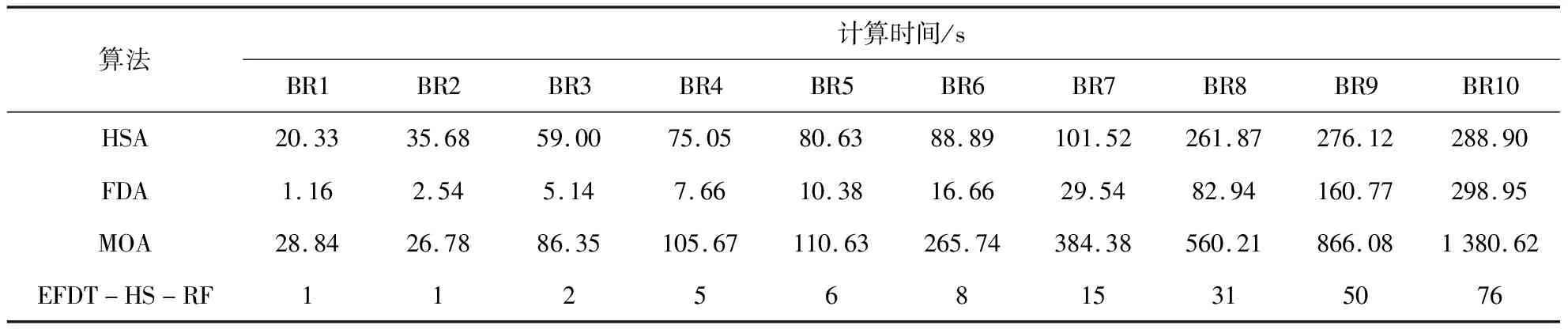
4 结 语

