改进的ARIMA模型预测精度分析
闵 盈 盈
(哈尔滨商业大学 计算机与信息工程学院,哈尔滨 150025)
时间序列ARIMA预测模型如下式所示:
yt=φ1yt-1+φ2yt-2+…+φpyt-p+et-
(θ1et-1+θ2et-2+…+θqet-q)
(1)
ARIMA模型在预测中都只是对某个时间点进行的研究,然而有时对未来的影响不仅是一个点的效应,更是一段时间积累而导致最后结果变化.所以我们不访考虑一段时间上对ARIMA模型进行改良.基于数值分析中的Nowton-Cotes求积公式又称等距节点公式,对一时间段上的数据作近似计算,提高计算精确度,具体方法是:
利用等距节点公式
(2)

(i=0,1,…,n)

式(1)变为:
(3)

1 模型拟合程度分析
模型拟合程度分析,主要应用回归分析最小二乘法,建立一元回归方程:y=a0+a1x,其中y为预测值,x为实际值,建立实际值xi和预测值yi之间的实数对(x1,y1),(x2,y2),…,(xn,yn),其中n为预测期数,通过时间序列预测值和实际值拟合系数a0和a1,则模型的拟合程度就通过回归方程的精确度表现出来,具体做法如下[3].
1.1 分阶段拟合程度分析
把三个模型命名为a,b,c,依次表示改进前ARIMA模型、改进后ARIMA模型和指数平滑模型,为了更加精确的分析拟合程度[4],把每个模型的预测值和实际值分为三个阶段,命名为s1,s2,s3,三个模型的预测值记为ya,yb,yc,具体数据如表1所示.

表1 三个模型预测值与实际值对照表第一阶段s1
如表2所示,JB统计量显示三个模型三个阶段都接近正态分布,偏度统计量在第二阶段的b模型和c模型出现负值,也就是出现了向左的长拖尾,其余情况都是向右的长拖尾,峰度统计量全部小于3,模型曲线比较平坦,说明拟合情况都不错.如表2所示第三阶段b模型,相关系数最高达到0.997 254,同时F统计量最大,达到4 357.658,拒绝原假设,模型拟合最好,拟合度最高.其次拟合情况最好的是第三阶段指数平滑模型,但拟合情况最不好的也是指数平滑模型的第一阶段,说明指数平滑模型比较适合25 a以上的预测,而改进前时间序列ARIMA模型三阶段都表现平平,改进后时间序列ARIMA模型在三个阶段均表现良好,说明适合各个阶段的预测[5-6].

表2 三个模型三个阶段回归分析表
1.2 整体拟合程度分析
以上分析了三个阶段模型的拟合程度,下面看一下三个模型的拟合情况,见图1.同样应用一元回归最小二乘法分析作图.

图1 a、b、c模型预测值与实际值序列图
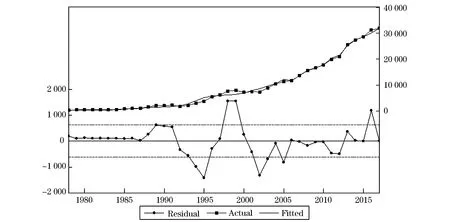
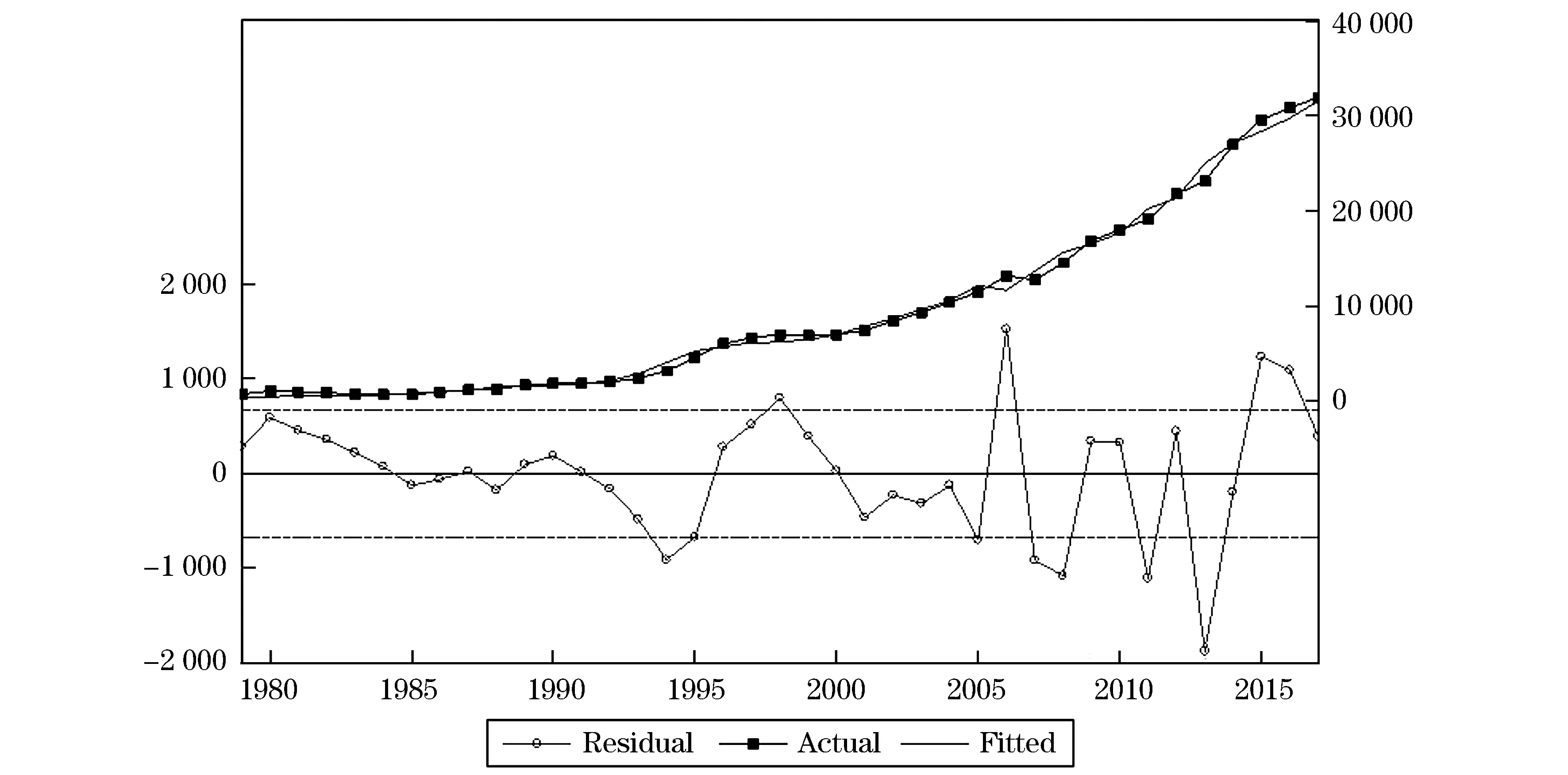
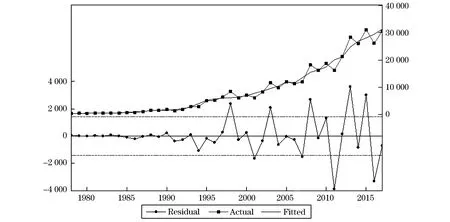
如图1所示,JB统计量显示三个模型都接近正态分布,其中b模型最为接近,c模型其次,a模型最弱,偏度统计量均为正值,都是向右的长拖尾,峰度统计量全部小于3,但非常接近于3,三个模型曲线都比较平坦,其中b模型最为平坦,c模型其次,a模型最弱,拟合情况都不错.一元回归分析图所示,拟合最好的是b模型,其次为c模型,最弱的是a模型,同时查看三个模型预测值与实际值序列图,SR为实际值,QIAN为改进前时间序列ARIMA模型预测值,HOU为改进后时间序列ARIMA模型预测值,ZHI为指数平滑法预测值,三个模型与原始序列SR最为接近几乎重合的是b模型,其次是c模型,最不好的a模型.如表3所示三个模型中b模型的相关系数最高达到0.995 931,同时F统计量最大,达到9 301.061,残差平和最小为14 645 284,依次排序为相关系数a>c>b,F统计量a>c>b,残差平方和a 表3 三个模型回归分析表 通常用预测误差来衡量预测精度,预测误差有五种衡量指标,下面就定量分析三种模型的预测误差. 三个模型具体的确度衡量指标如表4所示. 表4 三个模型预测精度分析表 图3 b模型预测值、实际值与残差序列图 图4 c模型预测值、实际值与残差序列图 如表4、图2~4所示三个模型精度度量数据,数据表明绝对误差的平均值b 图2 a模型预测值、实际值与残差序列图 本文主要基于指数平滑法中的双指数平滑应用城镇居民平均收入年度数据进行预测研究,从模型拟合程度、精度度量指标对比分析改进前后时间序列ARIMA模型和指数平滑预测模型,结果显示改进后时间序列ARIMA模型预测最为精确,其次为指数平滑法的预测模型,最后为改进前时间序列ARIMA模型预测.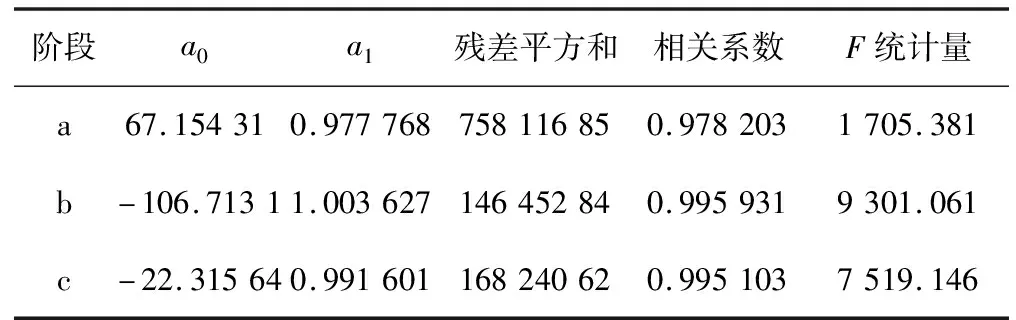
2 模型精确性指标分析

3 结 语

