OFDM序列调制的信息分组映射方法研究

阎肖鹏，冯旭东，付 军

(中国人民解放军91550部队，辽宁 大连 116023)

0 引言

序列调制[1](Index Modulation，IM)，又称为序号调制，是近年来被广泛研究的一种新型调制技术，其可看作是广义空间调制(General Spatial Modulation，GSM)中基于天线组合的信息承载方法向全信息传输要素的一种推广[2-4]。在IM技术中，通信系统中任意种类的数量为2个以上的传输要素均可用于加载信息，如天线、子载波、中继节点、调制种类、时隙/采样间隔、预编码矩阵和扩频码等。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)是目前应用最广泛的多载波技术，其在频谱利用率、抗多径和易于实现等方面具有明显优势，其缺点是多路时域叠加信号的峰均功率比(Peak-to-Average Power Ratio，PAPR)较高。OFDM序列调制(OFDM with Index Modulation，OFDM-IM)是IM与OFDM的结合，其通过选择若干个子载波的组合并调制来加载信息，在相同的功率效率情况下，有望获得比传统OFDM更高的带宽效率，并可有效降低系统的PAPR[5-7]。

OFDM-IM方法从提出至今不过十年时间，还有很多理论问题和关键技术需要解决。在目前的OFDM-IM调制模型中，其原始信息分2次进行调制，第1次是选择子载波组合，第2次是对所选择的子载波进行正交振幅(Quadrature Amplitude Modulation，QAM)调制或多进制数字相位(Multiple Phase Shift Keying，MPSK)调制[8-14]。在这种方式下，2次调制是分别进行的，没有从系统可靠性入手对信息映射方式进行总体设计，导致调制信号间的最小欧式距离没有优化，影响了该调制方法的性能。本文对OFDM-IM的信息分组映射方法进行了研究，将APSK调制引入OFDM-IM中，针对其多圈星座图构建问题，结合APSK-OFDM-IM调制信号形式，提出了多圈穷举搜索的星座图构建方法，并以提升系统误码率性能为目标，提出了基于APSK-OFDM-IM的信息分组映射方法。

1 OFDM-IM调制模型

假设OFDM系统的子载波数目为n，在OFDM-IM方法中，一般将所有子载波均分为若干组，每个组再分别进行序列调制。假设将子载波分为g组，在每组内进行序列调制，选出的子载波再进行传统数字调制。每组子载波数为n/g，每组中选出k个子载波，这k个子载波进行l进制的数字调制，则一次调制可承载的信息量p为：

p=g(⎣lbC(n/g，k)」+lbl)。

每个小组的信息量为p/g，令p1=⎣lbC(n/g，k)」，p2=lbl，则p/g=p1+p2。在OFDM-IM的2组信息映射中，第1组映射加载p1比特的信息，第2组加载p2比特的信息，在完成信息映射分组后，采用传统OFDM的FFT方法，即可完成载波调制，后续流程与传统OFDM方法一致。OFDM-IM调制的基本流程如图1所示。

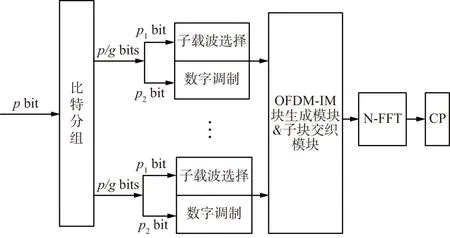
图1 OFDM-IM调制的基本流程Fig.1 The schematic diagram of OFDM-IM

假设子载波数n=8，子载波数索引集合为{1，2，3，4，5，6，7，8}，分组数g=2，则每组4个载波，每次参加序列调制的子载波数k=2，则p1=⎣lbC(n/g，k)」=2。对于每个子载波，再采用4-PSK或QAM调制。在第1组中，信息比特与子载波索引组合的对应关系如表1所示。

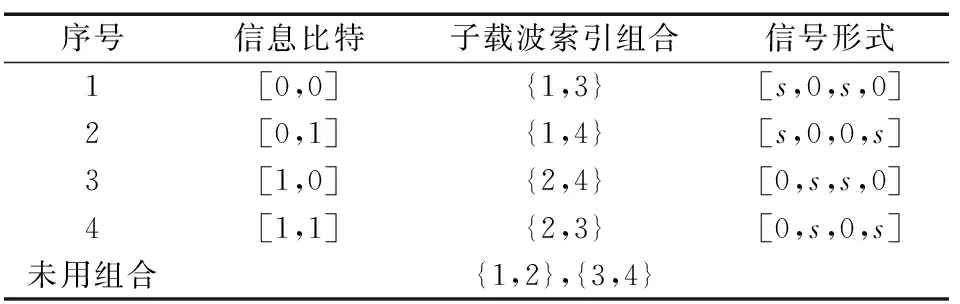
表1 信息比特与子载波组合对应关系表Tab.1 The relationship between the information bit and sub-carrier combination

需要说明的是，为了提高系统的误码率性能，当lbC(n/g，k)不是整数，即可选的脉冲组合有冗余时，一般选择载波中心频率相差较远的脉冲组合。如表1中，{1，2}和{3，4}这2组脉冲组合是未用的。

2 基于APSK调制的信息分组映射方法

在OFDM-IM调制方法中，数字调制部分一般对各个子载波单独进行QAM或MPSK调制，再生成子载波调制信号并交织。对于OFDM-IM调制方法，由于每次调制无法利用所有子载波，为了达到与OFDM相同的频谱效率，就需要对每个子载波进行更高进制的PSK或QAM调制。在各子载波数字调制这一环节中，现有的OFDM-IM方法采用传统MPSK或M-QAM调制方法，MPSK主要是将调制星座图中的单元圆进行等间隔取点，以获得代表各相位的调制信号，而M-QAM方法一般采用等幅度矩形星座图的方式，获得各调制信号形式。上述2种方法对传统OFDM信号可达到最优的误码率性能，由于OFDM-IM信号各子载波并不是等间隔分布，仍采用单一幅度等间隔划点或等间隔幅度的方式进行调制信息向子载波的加载，将导致系统误码率性能降低，同时，在高传输速率要求下，仍采用传统数字调制方式的OFDM-IM信号将具有较大的PAPR。

为解决上述问题，这里将APSK调制引入OFDM-IM中，提出了APSK多圈分组信息映射方法。对于APSK调制，首先要确定其星座图分布，星座图分布确定后，其信息映射方式也就确定了[15]。这里针对OFDM-IM调制信号的形式，对APSK调制星座图重新进行了设计。由于OFDM-IM调制的理论误码率性能由调制信号的最小欧式距离决定，这里以最小欧式距离最大化为目标，对其星座图进行了设计。

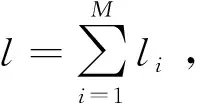
① 根据子载波数目k和调制阶数l，确定APSK的调制圈数M=「lbl/2k⎤；

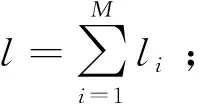
④ 确定各相邻圈的旋转角度，对于第i圈和第i+1圈，第i+1圈的旋转角度Δθi，i+1=π/LCM(li，li+1)，i=1，2，…，M-1；

⑤ 计算每次遍历所得调制信号的最小欧式距离，记录其最大值所对应的各圈调制阶数和半径的组合，即为最优星座图组合。

基于APSK调制分组映射的OFDM-IM调制方法原理如图2所示。

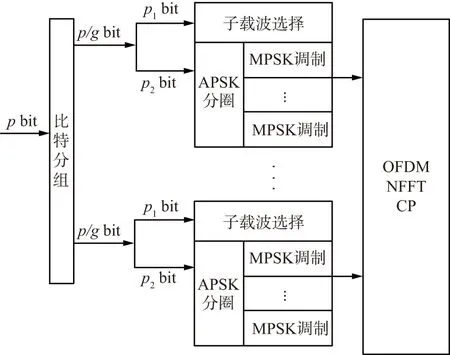
图2 基于APSK分组映射的OFDM-IM方法原理Fig.2 The schematic diagram of OFDM-IM based on APSK grouping mapping

该方法中，比特分组后，一部分进行子载波序列调制，另一部分进行APSK分组映射。APSK分组映射中，首先需要按照上述搜索步骤确定APSK最优星座图设计；在确定APSK最优星座图组合后，APSK分圈策略也相应确定，对于APSK的每一圈内，星座点采用等间隔方式划分，即相当于MPSK调制。根据APSK的星座图分布，再在每一圈上分别进行MPSK调制，从而完成该组子载波的数字调制。在完成该组序列调制比特映射后，后续步骤与OFDM-IM相同。

3 算法仿真与分析

为了验证算法的可行性和准确性，在Matlab仿真环境中，对该方法的性能进行了仿真分析，并与相同频谱效率的QAM-IM-OFDM调制方法进行了比较。

假设子载波数n=8，子载波数索引集合为{1，2，3，4，5，6，7，8}，分组数g=2，则每组4个载波，在参加序列调制的子载波数k=2，数字调制进制数l=16，以及k=3，l=32两种情况下，分别对APSK星座图进行了设计，并给出了相应的信息分组映射方案。2种情况下构建的APSK分圈如表2所示。

表2 最优多圈APSK星座图参数Tab.2 The optimal parameters of APSK multi-ring constellation

在调制子载波数k=2，数字调制进制数l=16，APSK分组映射方法采用表2中第1行的星座图，此时第1，2圈之间的旋转角度Δθ1，2=π/8。对APSK分组映射方法、传统QAM和MPSK三种方法下的OFDM-IM误码率性能进行了仿真，结果如图3所示。

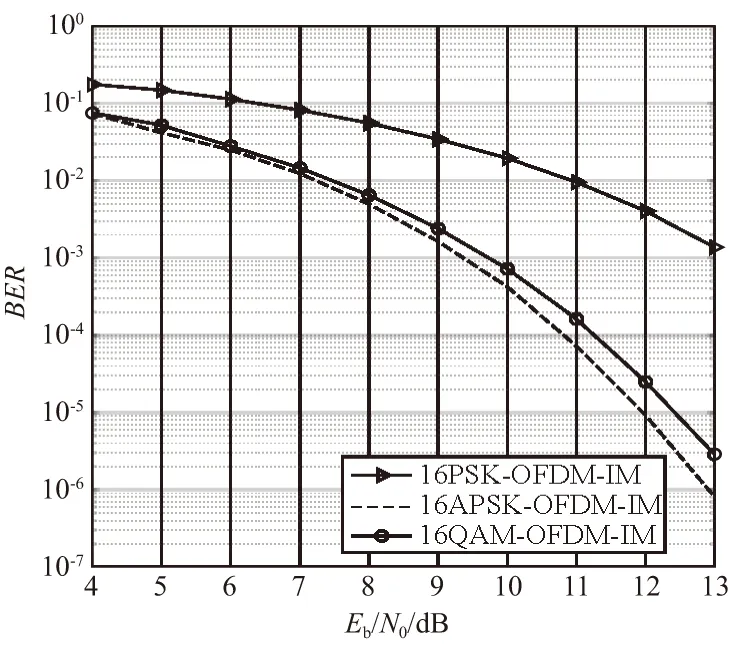
图3 16进制时3种典型OFDM-IM调制的 误码率性能仿真结果Fig.3 The BER simulation results of three OFDM-IM hexadecimal modulations

由图3可知，在16进制情况下，与16PSK-OFDM-IM调制方法相比，APSK分组映射方法的误码率性能有较大优势，在Eb/N0=12 dB情况下，其误码率性能有2个数量级的优势。在BER=10-5情况下，APSK分组映射方法相对于16QAM-OFDM-IM调制方法有较小优势，约为0.5 dB，且优势随信噪比的升高而增加。

在调制子载波数k=3，数字调制进制数l=32时，对APSK分组映射方法和传统QAM和MPSK调制方法下的OFDM-IM的误码率性能进行了仿真，结果如图4所示。APSK分组映射方法采用表2中第2行的星座图，此时第1，2圈之间的旋转角度为Δθ1，2=π/247。

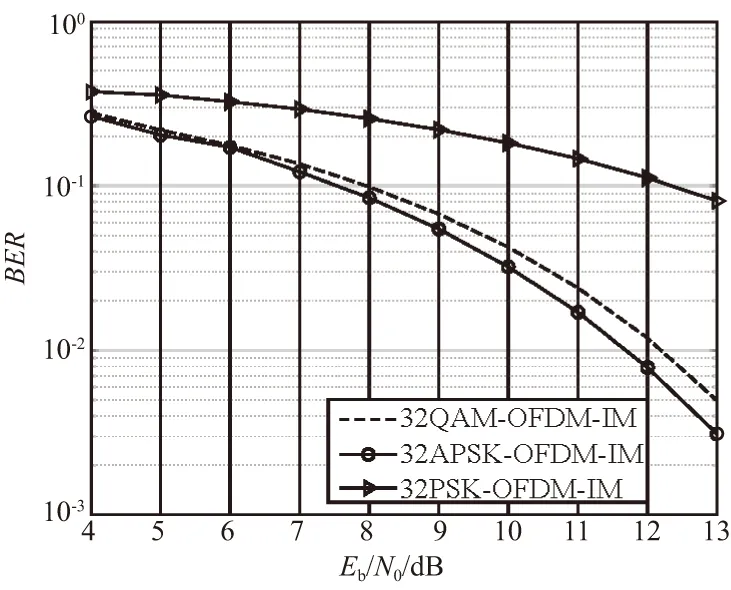
图4 32进制时3种典型OFDM-IM调制的 误码率性能仿真结果Fig.4 The BER simulation results of three OFDM-IM 32-ary modulations

由图4可知，在32进制情况下，与32PSK-OFDM-IM调制方法相比，APSK分组映射方法的误码率性能有较大优势，在Eb/N0=12 dB情况下，其误码率性能约有一个数量级的优势。与16进制情况下的仿真结果类似，APSK分组映射方法相对于QAM-OFDM-IM调制方法有较小的优势，且优势随信噪比的升高而增加。综合以上2次仿真结果可以看出，与OFDM-IM所采用的传统多进制调制方法相比，APSK分组映射方法增加了OFDM-IM调制信号的最小欧式距离，提升了系统的误码率性能。

4 结束语

载波序列调制方法在提高系统调制容量上具有明显的优势。目前，针对载波序列调制所用的二级信息映射模式展开研究，为进一步提升系统误码率性能，提出了基于APSK调制的信息分组映射方法，建立了相应的APSK多圈星座图优化模型，给出APSK-OFDM-IM的原理框图。仿真结果表明，与OFDM序列调制二级信息映射方法相比，该方法可提高调制信号的最小欧式距离，有效提升系统的误码率性能，具有较好的应用前景。