基于残差神经网络的通信混合信号识别
董 聪,张传武,高 勇
(1.四川大学 电子信息学院,四川 成都 610065;2.电子信息工程(西南民族大学)国家民委重点实验室,四川 成都 610225)
0 引言
通信信号的调制识别在军事和民用领域具有重要意义[1-2]。传统的单信号调制识别算法主要分为2大类[3]:基于决策理论的最大似然假设检验方法[4]和基于特征提取的模式识别方法[5-6]。混合信号单通道需要识别的信号有2类:对称混合信号和非对称混合信号。本文研究前者,对称混合信号识别主要有2类方法。Lu[7]、EI-Mahdy[8]等人,先将接收信号分离开,然后使用传统的单信号识别方法对分离后的信号进行调制识别,该方法默认接收信号是混合信号。这是第一种方法,这种方法本质上仍是单信号识别,识别结果更依赖于分离效果。高玉龙以循环谱为出发点,利用BPSK、QPSK和OQPSK信号在某些循环频率上的差异来提取信号特征[9],但是仍然要求先进行预处理将信号进行分离;另一类方法是直接从接收混合信号出发进行识别[10],是一种真正意义上的混合信号识别方法。该论文研究了共用同一信道中未知信号的调制识别问题,但是该方法必须已知一个信号调制类型且假定已知信号采用矩形成型,当信号采用升余弦成型时识别性能会恶化。
本文应用残差神经网络(Residual Neural Network)模型对通信混合信号进行调制识别。在保证识别率的前提下,此算法不需要对输入数据进行预处理,不需要人工定义识别特征,并且对信号的码元速率、频偏和相偏具有一定的适应性。
1 调制信号模型
通常发射通信信号序列可以表示为:
(1)
式中,An,ωc,φn,θ分别表示第n个符号的幅度、频率、相位以及初始相位;g(t)表示脉冲成型函数;T表示符号周期。
接收信号的表示形式为:
(2)
式中,hn(t),ω0分别表示信道响应和接收机的频率。
本文所用信号数据集有频移键控(FSK)和相移键控(PSK)。
FSK通过载波频率变化来传递数字信息,M进制频移键控数学表达式为:
ωn∈{ω1,ω2,...,ωM},
(3)
式中,g(t)同上;ωn表示第n个符号的频率;θ为初相。
PSK通过载波相位变化来传递数字信息,振幅及频率保持不变。
M进制PSK信号可以表示为:
k=1,2,...,M,
(4)
M一般为2k,其余变量同上。
2 基于残差神经网络的识别算法
2.1 残差神经网络
深度学习的不断发展,神经网络模型的深度也随之不断加深。但是实验结果表明,单纯地增加神经网络深度会带来梯度消失或爆炸的问题,为解决这个问题,残差神经网络(Residual Neural Network)被提出[11],它可以有效解决因为梯度爆炸而导致深层卷积神经网络出现的退化问题,并且能够保持良好的泛化能力。
残差模块 (Residual Block) 构建了ResNet ,该模块通过增加“快捷连接”(Shortcut Connections)实现。假定某段神经网络的输入为x,实际的输出为H(x),如果使用深层非线性网络来拟合非线性映射关系F(x)=H(x)-x,那么F(x)+x就可以表示为实际的输出H(x),而F(x)+x能通过带有“恒等变换 (Identity Transformation)”的神经网络实现。残差块结构如图1所示。

图1 残差块结构Fig.1 Residual block structure
浅层的残差模块由2层组成,即
F(x)=W2σ(W1x),
(5)
H(x)=F(x,{W1,W2})+x,
(6)
式中,σ表示非线性函数ReLU;W1,W2表示权重。残差模块增加的恒等映射(Identify Mapping)不会额外增加参数和计算量,但是却能大大提高神经网络模型的训练速度。这是因为,相比于使用深层的非线性网络去拟合隐藏的非线性映射H(x),残差模块目的在于使残差F(x)尽可能小,这样整个ResNet只需要学习输入、输出差别即残差部分,简化了神经网络的学习难度。
本文中ResNet网络参数设置如表1所示。
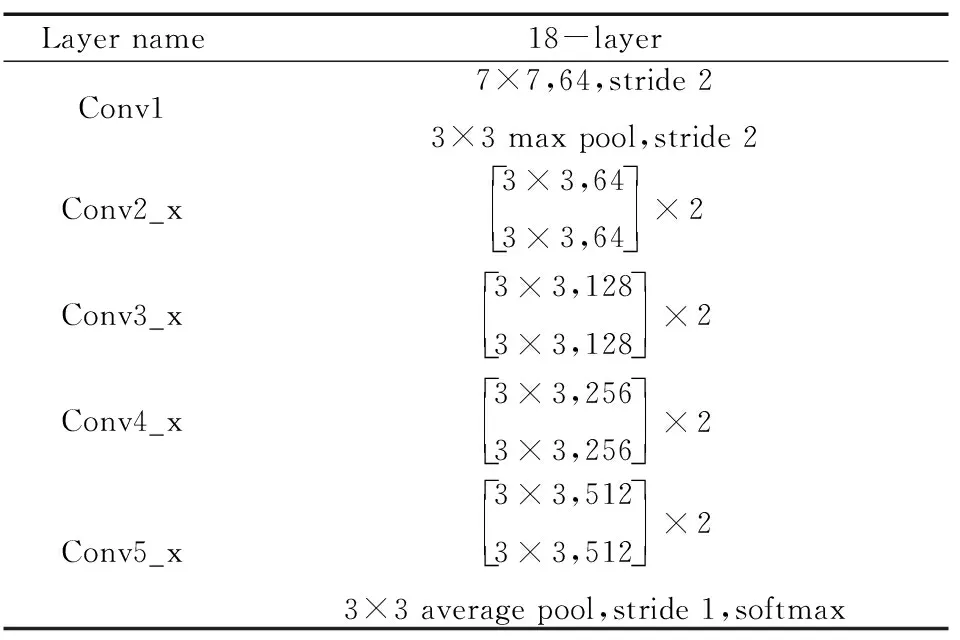
表1 ResNet网络参数设置Tab.1 ResNet network parameter settings
2.2 随机梯度下降优化算法
神经网络中所有的输出以及代价函数均由输入和参数求得,在得到相应输出及代价函数的情况下,还需要通过优化算法来减小代价函数,得到优化后的参数和权值。一般的优化算法为梯度下降法(Gradient Descent),算法的表达式为:
(7)
式中,J(βn)为损失函数;η为学习率。
梯度下降会同时计算所有数据的梯度值,但在实际中,要处理的数据量通常非常巨大,而硬件资源的有限使得难以实现大数据的梯度计算,而且耗时较长。在不降低网络学习效果的前提下,本文采用了随机梯度下降算法(Stochastic Gradient Descent)来提高网络模型的训练速度。该算法的梯度计算以及参数更新是利用每次从数据集中随机选取一个样本而不是全部训练数据的损失函数,也就是该算法优化的是每一次迭代中某一条训练数据而不是全部数据的损失函数,这样一来每一次迭代网络参数更新的速度就会大大提高。
2.3 算法流程
基于ResNet网络模型的调制识别算法流程分为训练和测试两个过程,大概流程图如图2所示。
训练过程为:
① 训练数据是仿真生成的调制信号,它首先格式转化为Ndarray类型,再输入到ResNet网络模型中;
② ResNet网络模型通过信号特征对训练数据进行分类识别,然后输出算法对各信号调制方式的识别结果;
③ 将各信号调制方式的识别结果与输入ResNet网络的训练数据的标签,也就是信号实际的调制方式进行对比,利用代价函数计算出识别结果的误差。根据最终误差的大小以及利用梯度下降的反向传播来更新和改进ResNet的网络参数。
上述训练过程反复迭代,由于信号识别结果的误差会不断减小,算法对信号的识别准确率就随之不断提高,网络模型参数也将会逐渐接近于最优值,最终误差趋向于一个稳定值不再减小,此时表明网络已经收敛,训练停止。
测试过程:在ResNet网络模型训练完成之后,算法就可以直接对待识别信号的调制方式进行识别,待识别信号经过格式转化后,直接输入到ResNet中,ResNet网络模型将会使用训练好的网络参数提取特征和分类识别,最终输出识别结果。算法原理框图如图2所示。

图2 算法原理框图Fig.2 Algorithm principle block diagram
2.4 实验结果及其分析
为了验证本文所提出的基于残差神经网络的通信混合信号的识别率。本文利用MXnet深度学习平台,采用18层残差神经网络(ResNet)和卷积神经网络(CNN),分别在计算机上进行了验证。计算机CPU型号为Inter(R) Core(TM) i7-8700 CPU @3.2 GHz 3.19 GHz 16 GB内存。GPU型号为NVIDIA GeForce RTX 2080。
本文待识别的信号调制方式有:2FSK+4FSK,BPSK+2FSK,BPSK+4FSK,BPSK+BPSK,BPSK+QPSK,QPSK+2FSK,QPSK+4FSK,QPSK+QPSK,其中混合信号中两分量信号的幅度均为1,信噪比范围为-10~10 dB,以2 dB为间隔。采样倍数选取4倍采样,脉冲成型滤波器滚降系数设为0.35,码元速率fb、载波频率、初始相位分别在50~200 Kb/s、 ±0.05fb、0~π/8范围内随机选择。每种信号调制方式产生5 000个样本,这些样本中,4 000个为训练数据,1 000个为测试数据。基于ResNet网络损失函数下降曲线图如图3所示。
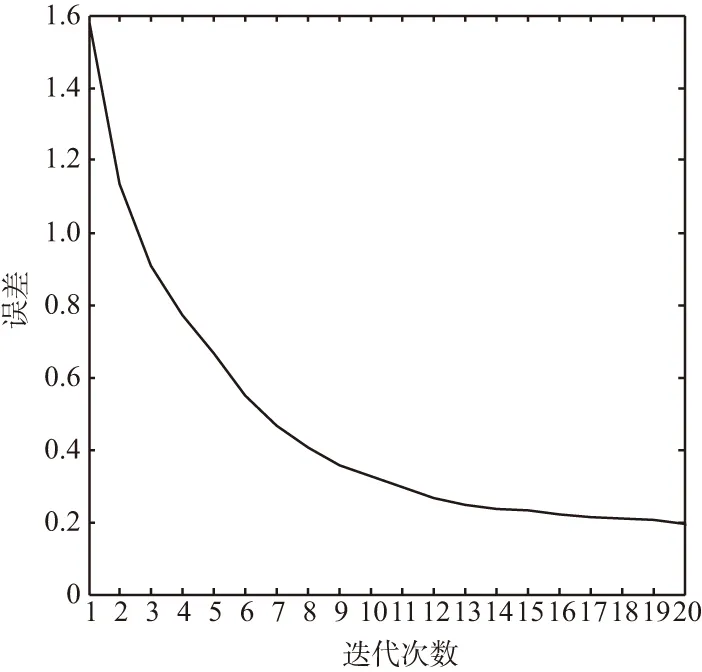
图3 基于ResNet网络损失函数下降曲线Fig.3 Loss function drop graph based on ResNet network
从图3可以看出,损失函数在接近第18次迭代时基本上不再减小,可以认为此时神经网络模型的学习过程已经收敛。
在ResNet和CNN网络下的各混合信号识别性能曲线如图4和图5所示。

图4 基于ResNet识别率性能曲线Fig.4 Recognition rate performance graph based on ResNet
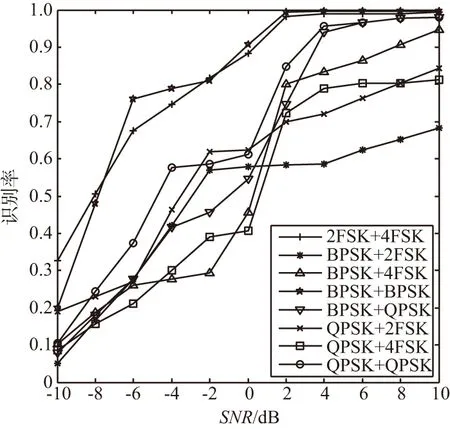
图5 基于CNN识别率性能曲线Fig.5 Recognition rate performance graph based on CNN
从图4和图5可以看出,无论是基于残差网络还是CNN网络,随着信噪比的增加,信号的识别率也随之增加。在信噪比为4 dB以上时,基于残差网络下识别率高达90%以上。而基于卷积神经网络下,即使信噪比为10 dB,BPSK+2FSK,QPSK+2FSK,QPSK+4FSK三种混合信号也未能较好地识别。
基于CNN和ResNet平均识别率对比曲线图如图6所示。从图中可以看出,在同一信噪比下,基于ResNet的识别算法比基于CNN的识别算法识别率高。这是因为,传统的卷积层在进行信息传递时,会带来信息丢失、损耗的问题。ResNet 通过增加“恒等映射 ”(Identity Mapping)有效解决了这个问题,它将深层的非线性网络去拟合隐藏的非线性映射问题转化为学习输入、输出差别即残差的问题,提高神经网络的学习效率,也保护了信息的完整性。
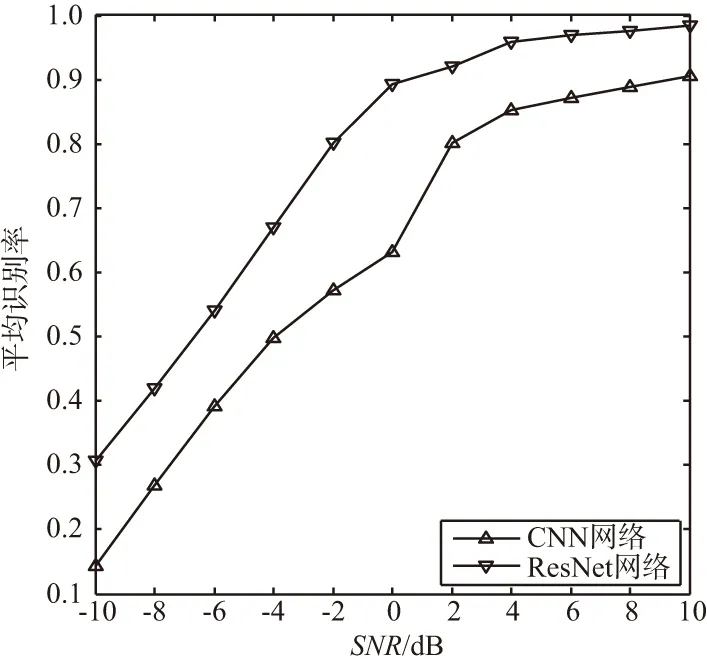
图6 基于CNN和ResNet平均识别率对比图Fig.6 Average recognition rate comparison based on CNN and ResNet
3 结束语
混合信号单通道识别是混合信号单通道处理需要解决的第一个问题。本文应用残差神经网络模型来解决通信混合信号调制识别的问题[12]。在信噪比4 dB以上能对2FSK+4FSK,BPSK+2FSK,BPSK+4FSK,BPSK+BPSK,BPSK+QPSK,QPSK+2FSK,QPSK+4FSK,QPSK+QPSK八种混合信号有较好的识别效果。不需要先验知识,避免了复杂的预处理过程,并且在一定范围内对信号码元速率、相偏和频偏不敏感,具有较强的适应能力。

