雷达-红外分布式融合多目标跟踪算法

张万顺，张安清，齐海明

(1.海军大连舰艇学院 学院五大队， 辽宁 大连 116018；2.海军大连舰艇学院 信息系统系， 辽宁 大连 116018；3.海军91202部队，辽宁 葫芦岛125004)

0 引言

现代化战争条件下，信息能的释放将直接影响军队的作战能力，信息的采集和处理能力至关重要。雷达由于能够提供完整的目标位置信息和多普勒信息，成为战场上信息采集的重要传感器，但随着电子对抗、反辐射导弹、超低空突防和隐身战机等技术的发展，其探测能力和生存空间受到限制，单一类型的传感器探测系统已无法适应现代战场的复杂环境。相比之下，红外传感器作为被动传感器，无需向外辐射能量，天生具有“四抗(电子对抗、反辐射导弹、超低空突防、隐身战机)”的优势，具有高精度角度量测等优点，但存在无法获得目标距离信息，受大气影响大等不足。将二者结合可以优势互补，大大提高探测系统的鲁棒性以及对目标的跟踪能力。

现有的雷达红外数据融合算法多为集中式融合结构[1-4]，文献[4]采用激光雷达测距为红外传感器补充距离信息完成目标跟踪，红外传感器无法在无线电静默时单独完成跟踪任务，同时集中式融合结构通信代价高，容易出现单点错误，网络延展性差。现有的分布式融合结构的多目标跟踪算法，多采用传统的目标跟踪算法(如卡尔曼滤波及其扩展算法)，需要进行复杂的点迹关联和数据对准[5-6]，文献[7-8]讨论了同质传感器分布式融合的PHD滤波算法。

采用分布式融合结构对雷达红外异质传感器数据进行融合，使探测器具有独立处理信息的能力，传送独立处理后的数据给融合中心，降低探测系统的通信量，增强系统的可靠性。对于雷达传感器，在直角坐标系和修正球坐标系(Modified Spherical Coordinates，MSC)结合的混合坐标系中引入GM-PHD滤波，实现多目标跟踪的同时避免了传统多目标跟踪算法复杂的点迹关联过程[9]，在直角坐标系中进行状态预测，在MSC中进行状态更新，使得量测方程和观测方程均为线性方程，且解决了量测噪声因坐标系转换而产生的相互耦合。对于红外传感器，在MSC中成功引入GM-PHD滤波，使红外传感器可以独立实现对多目标角度信息进行跟踪。雷达和红外的更新过程都是在修正球坐标系中完成的，便于将红外传感器的状态估计值作为量测值与雷达量测进行融合。

1 雷达混合坐标系GM-PHD滤波

在直角坐标和修正球坐标结合的混合坐标系中使用GM-PHD滤波，实现在目标数目可变情况下的多目标跟踪，并对目标数目进行估计。

1.1 GM-PHD滤波

PHD滤波用基于随机有限集的Bayes滤波解决多目标跟踪问题[10-11]，其物理意义是状态空间中目标数的后验强度，其在状态空间的积分为目标个数，目标状态则为对应峰值。其预测和更新方程如下：

ps，k(ξ)fk|k-1(x|ξ)]Dk-1(ξ)dξ，

(1)

Dk=[1-pD，k(x)]Dk|k-1(x)+

(2)

式中，Dk|k-1(x)为多目标先验密度pk|k-1(x|zk-1)的PHD；x为k时刻单个目标状态；ξ为k-1时刻单目标状态；γk(·)为新生目标PHD；βk|k-1(·|·)为衍生目标RFS的PHD；ps，k为目标存活概率；gk(·|·)为单个目标似然函数；pD，k(·)为目标的检测概率；κk(z)为杂波PHD函数。

GM-PHD滤波算法的运动模型和观测模型都是线性的，量测噪声和过程噪声均服从高斯分布。此时观测空间内所有目标状态以高斯波的形式在状态空间叠加，形成全局PHD，表示为：

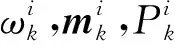
GM-PHD滤波算法的预测和更新方程如下：

Dk|k-1(x)=DS，k|k-1(x)+DD，k|k-1(x)+γk(x)，

(3)

等式右侧三项分别为存活目标、衍生目标和新生目标的预测PHD。

(4)

等式前项表示漏检目标的 PHD，后项表示检测到目标的更新 PHD。

1.2 混合坐标系雷达跟踪

在直角坐标系中进行状态预测，将预测状态转换成MSC，在MSC中进行状态更新，避免了因坐标系转换引起的非线性问题和量测噪声相互耦合问题。直角坐标系中离散线性状态预测方程：

(5)

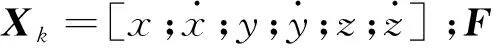
MSC中状态观测方程：

(6)

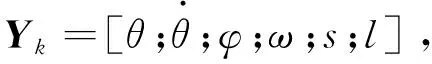
在MSC中，可充分利用雷达精准的距离量测和多普勒信息。直角坐标系和MSC的转换过程如下：

Y=LD-M(X)，X=LM-D(Y)，

(7)

(8)

协方差阵的转换关系为：

(9)

(10)

PHD的均值和协方差的递推可使用Kalman滤波原理。

2 修正球坐标系红外跟踪与数据融合

红外探测系统可以通过载机机动实现目标距离观测[12]，只是条件较为苛刻。在MSC中，前5个状态分量均可实时观测或计算[13]，当距离信息不可观测时，前5个状态分量与不可观测的第6个分量自动解耦，使得Kalman滤波接近无偏。在MSC中使用GM-PHD滤波实现单站红外传感器多目标纯角度跟踪，将红外估计值与雷达量测在融合中心进行时间配准并关联融合，用于对雷达状态预测的更新。

2.1 修正球坐标系红外角度跟踪

MSC中线性状态方程为：

(11)

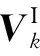
观测方程为：

(12)

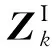
2.2 雷达红外数据融合

分布式雷达红外融合跟踪结构如图1所示。

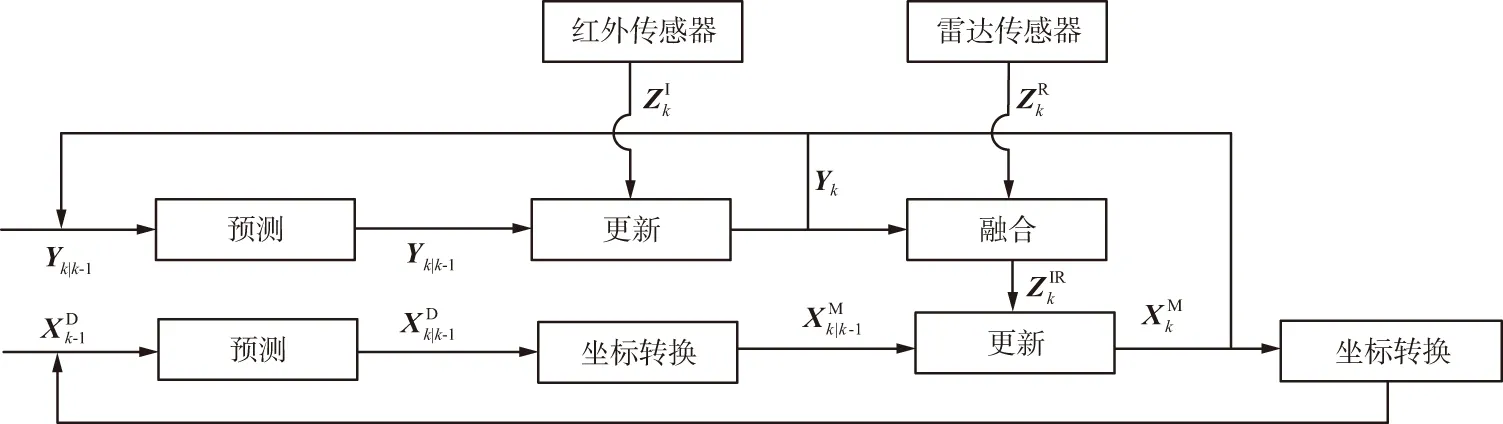
图1 雷达红外分布式融合跟踪结构Fig.1 Tracking structure of radar-infrared distributed fusion

雷达和红外传感器可单独实现滤波估计，红外传感器的状态估计值可以用观测矩阵提取出与雷达量测相对应的状态分量，与雷达量测进行时间对准。关联融合后，用融合量测值更新在MSC中的状态预测值，如果因雷达传感器漏检等原因使得关联失败，则可以直接用未经过融合的量测或红外估计值更新雷达状态预测，可大大降低探测系统漏检的可能性，更新得到的系统估计值返回给雷达和红外传感器进行下一时刻的滤波估计。

定义一个统计量：

(13)

(14)

(15)

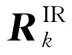
3 分布式融合仿真

3.1 仿真参数设定

因红外传感器单站不易获得目标距离信息，目前只适合非机动或弱机动目标的角度跟踪，可适用于跟踪远距离机动概率低的目标，所以此次仿真选择对匀速目标进行跟踪。假定检测区域中先后存在3个目标，目标信息如表1所示。

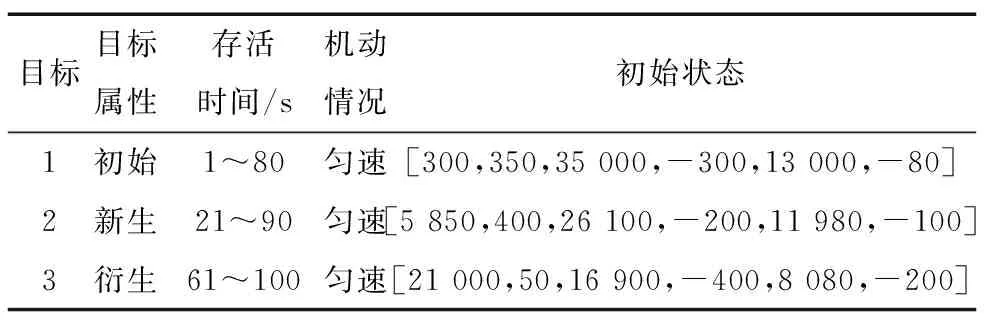
表1 目标信息Tab.1 Target information

监控时间100 s，采样间隔时间T=1s，假定雷达和红外传感器同地配置使用，仿真时雷达量测噪声协方差矩阵为：

红外传感器量测噪声方差阵为：

雷达过程噪声协方差阵为：

噪声控制阵为：

红外过程噪声协方差阵为：

噪声控制阵为：

雷达初始状态协方差为：

PR=diag[100，1，100，1，100，1]。

红外初始状态协方差为：

0.000 000 3 0.000 005 0.000 000 001)。

检测概率和存活概率设为0.98，杂波数符合均值为10的泊松分布，状态合并门限设为5，量测融合门限cor=3，最大高斯数100，用最优子模式分配(OSPA)距离进行性能评估[15]，c=10，p=2。

3.2 仿真结果分析

图2是使用表格1目标信息在三维空间建立的目标航迹以及杂波量测。

雷达红外融合的目标位置估计如图3所示。

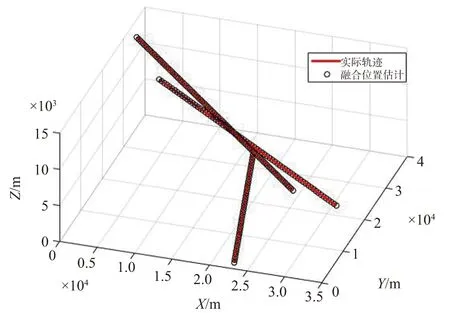
图3 雷达红外融合多目标位置估计Fig.3 Multi-target position estimation of radar-infrared fusion

由图3可以看出，该融合跟踪方法能够在杂波环境中且目标数目可变的情况下实现多目标跟踪。

用目标的角度数据画出的目标角度轨迹和角度估计如图4所示。红外传感器可利用系统反馈信息或独立完成目标角度跟踪，图中显示该方法可很好的对多个目标角度信息进行跟踪。

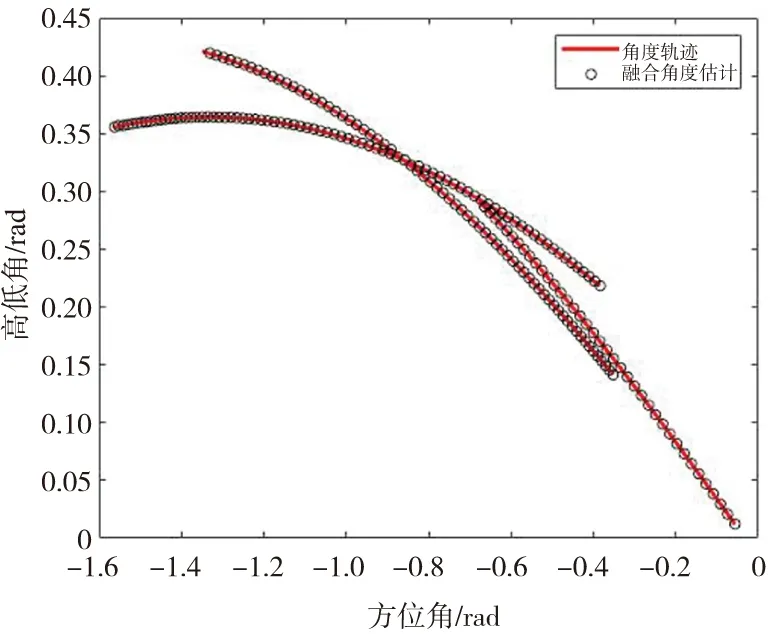
图4 雷达红外融合多目标角度估计Fig.4 Multi-target angle estimation of radar-infrared fusion

目标个数估计和OSPA距离统计如图5所示。

图5 目标个数估计和OSPA距离统计Fig.5 Target number estimation and OSPA distance statistics

目标个数估计部分显示，雷达独立跟踪会偶尔出现漏检或虚警，融合跟踪则大大降低了目标的漏检概率并大幅提高量测精度，可以对目标数目进行准确的估计，OSPA距离统计部分显示，当目标个数增加时，雷达传感器的跟踪精度受影响较大，而融合算法却能始终保持优良且稳定的跟踪精度。

4 结束语

现代战场电磁环境复杂，为了获得稳定可靠的多目标跟踪效果，异质传感器的数据融合受到广泛关注。现有的融合方式多采用集中式结构或传统滤波算法，本文提出雷达红外分布式融合多目标跟踪算法，采用GM-PHD滤波在混合坐标系和MSC中使雷达和红外传感器各自独立完成多目标跟踪，解决了因坐标系转换造成的非线性问题及量测噪声耦合问题，同时使得雷达红外量测在同一坐标系中以便于融合。仿真试验表明，雷达红外均可独立的完成多目标跟踪任务，二者配合使用取得了更加稳定更高精度的跟踪效果，大大提高了跟踪系统的可靠性和鲁棒性。