输油悬跨管道流致振动数值模拟研究

宋 微 王素玲 姜民政 隋 旭

（东北石油大学机械科学与工程学院）

长输管道受水流冲击后会由于基土的流失而浮出地面，导致管体在水流冲击下极易发生涡激共振，使管道产生疲劳破坏。 涡激共振是引发水下悬跨管道疲劳失效的最主要原因之一，有时即使管道应力、 应变处于校核的安全范围内，但由于涡激振动的原因仍会产生破坏，因此有必要研究其响应特性，避免共振现象的发生。

要对悬跨管道的振动特性进行分析，首先要对管道自振频率进行精确的计算。 20世纪90年代初Pantazopoulos就对管道产生涡激振动的理论及其发展进行了较为全面的介绍，他对以往学者们研究的涡激振动模型和相关试验情况进行了介绍和总结，并利用经验与试验相结合的方法给出了升力系数、旋涡脱落频率的频带带宽等参数的确定方法。 俞树荣等分析了海洋立管在流场作用下的受力特性，得到了自然频率和阵型的模态［1］。付冉等计算了内流对管道的动力响应，结果表明横向振动幅值明显增大［2］。目前，国内外学者大多集中在对单向流中管道振动情况的模拟，而利用数值模拟方法对悬跨管道涡激振动特性进行研究的则较少［3，4］。

笔者基于平面波动方程和声学振动理论，建立水下悬跨管道数值计算模型，考虑内外流体域与管道的流固耦合作用， 对比悬跨管道在干、湿模态下的振动情况，分析影响悬跨管道自振频率的相关参数及其变化规律。

1 数学模型的建立与计算

由于水和空气的密度不同，所以结构在水中和空气中的自振频率也不同且相差很大。 悬跨管道在不考虑流体作用时的固有频率通常认为是结构在真空中的频率，称为干模态［5，6］。 而在实际的环境中，管道处于水流中，水的密度较大，对结构频率具有一定的影响，而以往的研究中只考虑了管道在空气中的固有频率，而没有考虑管外水流和管内输送液体的作用，但这对涡激振动的影响是无法忽视的。

1.1 流体控制方程

涡激振动是典型的流固耦合问题，笔者将管外水流和管内流动液体考虑成声学流体，在此基础上计算管道的固有频率。 对于声学流体-结构相互作用的耦合问题，结构控制方程必须同时考虑流体动量N-S方程和连续性方程。

从质量守恒定律出发，连续性方程在全局笛卡尔坐标系下表示为［5］：

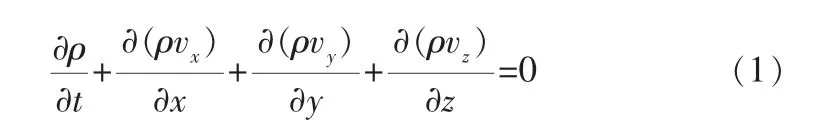
式中 t——时间，s；

v——速度矢量，m/s；

ρ——密度，kg/m3。

不可压缩粘性流体的N-S方程组表示为：

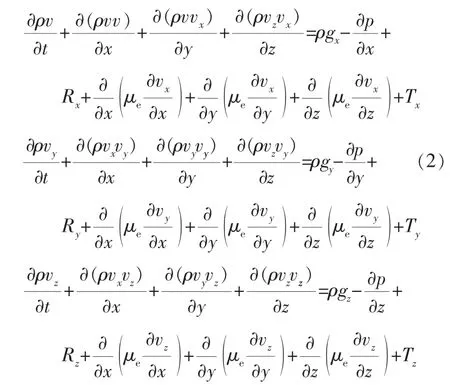
式中 g——重力加速度，m/s2；

p——声压，Pa；

R——分布电阻，Ω；

T——粘性损失项；

μe——有效粘度，Pa·s。

对连续性方程和N-S方程组进行简化可以得到波动方程：

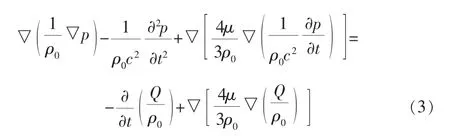
式中 c——流体介质中的声速；

Q——质量源；

ρ0——平均流体密度；

μ——动态粘度，Pa·s。

对波动方程在体积域内进行积分：

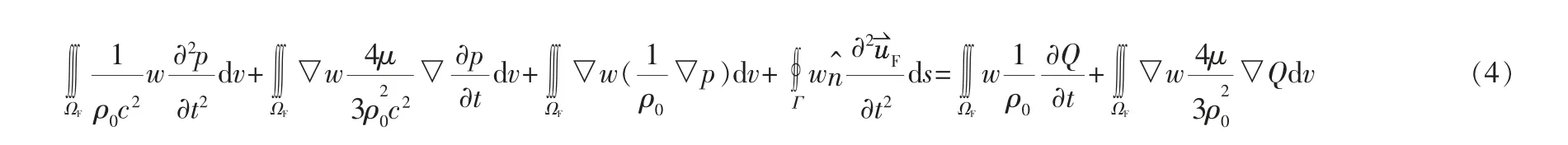
式中n——边界法向单位矢量；

ds——声域边界表面微分；

w——测试函数［7］；

ΩF——声学域；

Γ——声域边界。

流体离散化后，单元内压力和位移分量空间变化的有限元近似形状函数为：

式中 {N}——压力单元形状函数；

{N′}——位移单元形状函数；

{pe}——节点压力矢量；

u——位移分量空间变化的有限元近似形状函数。

变量的二阶导数和压力的虚拟变化可表示为：

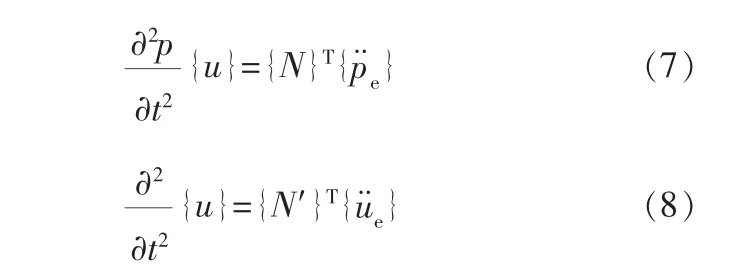
式中 ue——节点位移矢量，m。

将式（5）～（8）代入式（4）中，得到：

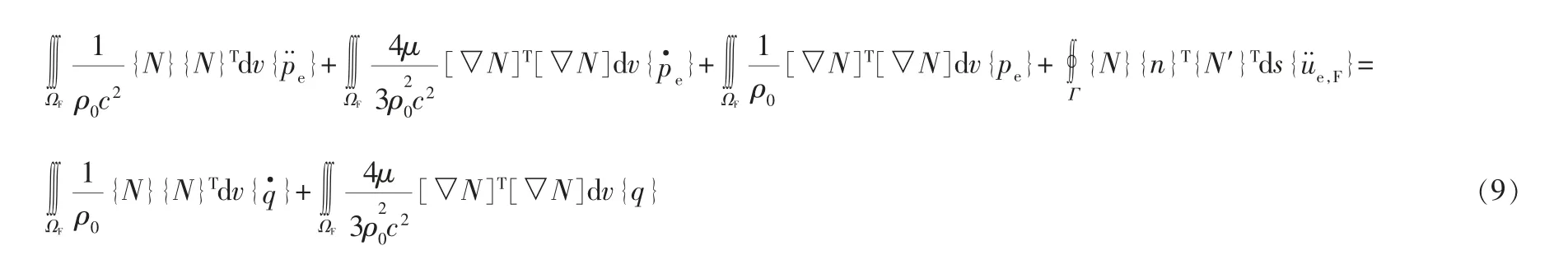
式中 {n}——流体边界外向法向量；

{q}——节点质量源向量；

{ue，F}——流体位移矢量，m。

流体内声场的有限元方程矩阵可表示为：

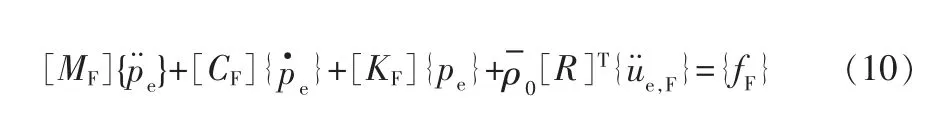
式中 ［CF］——声流体阻尼矩阵；

｛fF｝——声流体载荷矢量；

［KF］——声流体刚度矩阵；

［MF］——声流体质量矩阵；

［R］T——声流体边界矩阵；

1.2 结构控制方程

在水流冲击下管道后方的旋涡脱落会引起管道结构运动，对于弹性管道，通常采用有限单元法进行离散。 结构振动方程的离散形式为：

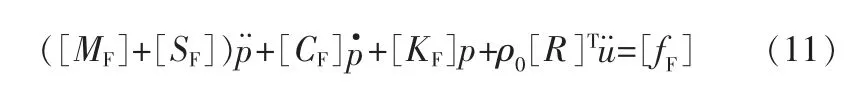
式中 ［SF］——声波晃动质量矩阵。

流固耦合界面S上的流体压力负荷向量是通过将表面积上的压力积分得到的，即：

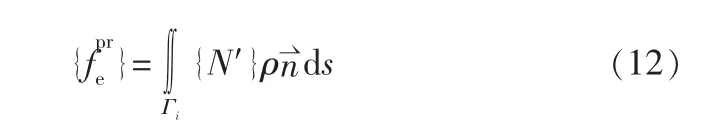
式中 {fepr}——流体压力载荷矢量，Pa；

Γi——流固耦合表面。

将式（8）中给出的压力近似有限元函数代入式（12），得到：

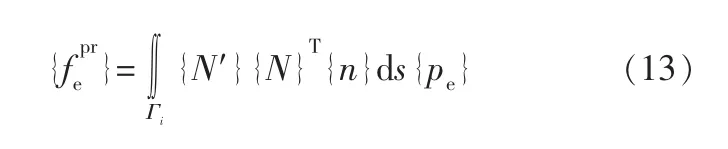
由式（10）、（13）得到：

将式（14）代入式（11）可得结构动力方程：

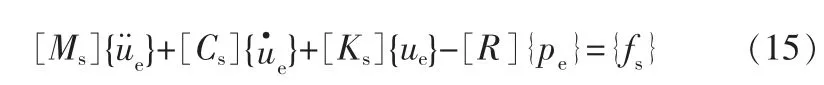
式中 ［Cs］——结构阻尼矩阵；

［fs］——结构载荷矩阵；

［Ks］——结构刚度矩阵；

［Ms］——结构质量矩阵。

式（10）、（15）即为描述声学流体-结构问题的完全有限元离散方程。

1.3 模型验证

采用ANSYS中Workbench ACT对悬跨管道进行有限元模态分析，管道输送介质为油、管外流体为水。 湿模态分析时将水和油考虑为声学流体，管道内外场声速分别为1 500、1 000m/s，管道内外壁设为两个流固耦合面（FSI面）。首先对内径为0.305m、壁厚为0.02m、悬跨长度为15m的管道建模。 管道材料为钢，泊松比为0.3，弹性模量为206GPa，密度为7 850kg/m3。其三维有限元模型如图1所示。

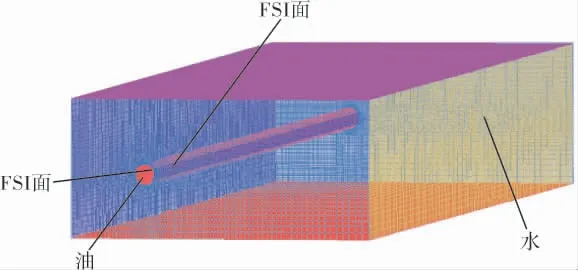
图1 悬跨管道三维有限元模型

升力系数和斯特劳哈数（St数）是判定数值模拟结果正确与否的重要评价标准。 首先对雷诺数为100时的静止管道进行数值模拟研究。 将计算得到的升力系数振幅Cl、平均阻力系数Cd、St数与雷诺数为100时的静止单圆柱数值模拟结果［8］相对比。 由表1可见，对静止单圆柱的模拟结果与经典实验结果［9］进行比较，模拟误差控制在合理范围内，验证了本项研究数值计算方法的正确性。

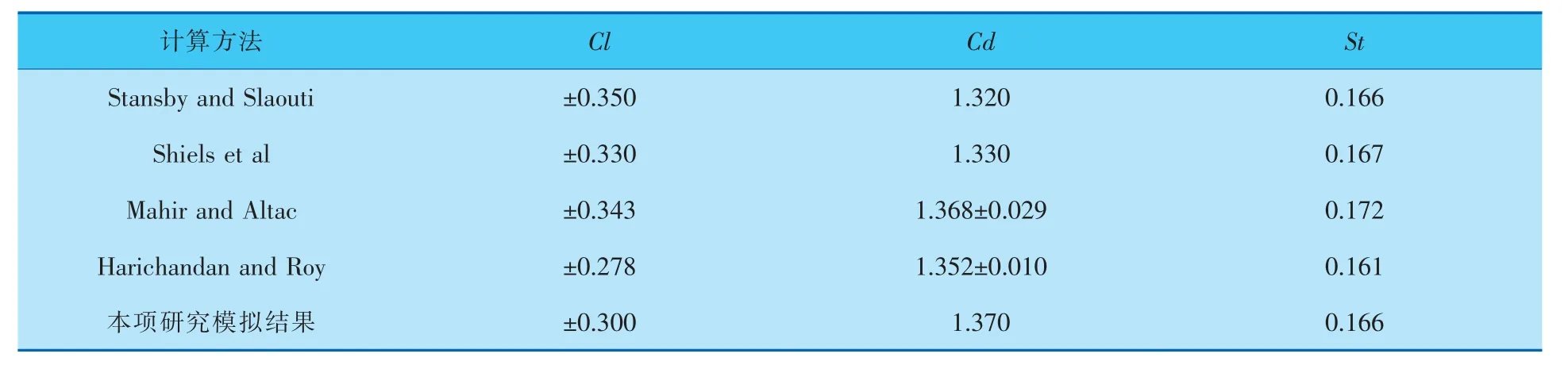
表1 升力系数振幅、平均阻力系数、斯特劳哈数的结果对比

干、湿模态的结果对比见表2，可以看出，湿模态下的自振频率更小、 更接近涡激振动频率，此时更容易发生共振现象，因此必须考虑内外流体与管道的耦合作用，防止发生共振。

表2 干、湿模态的结果对比

2 水下悬跨管道涡激振动破坏影响因素分析

2.1 雷诺数对悬跨管道振动的影响

以静止管道绕流为初始流场，分别对雷诺数为80、90、92、100、120、140、160时的悬跨管道 进行绕流情况分析。 由图2（分别以旋涡脱落频率与管道固有频率的比值ft/fn、管道横向运动振幅与直径的比值A/D作为纵坐标）可以看出，当雷诺数小于80时，管道横向运动振幅不明显，旋涡脱落频率ft与管道固有频率fn还有很大差距，此阶段处于非锁定阶段；当雷诺数增大到90时，管道的运动幅度有明显增加，旋涡脱落频率开始接近管道固有频率，此阶段为过渡阶段；当雷诺数继续增大到92时，旋涡脱落频率逐渐增大并接近管道固有频率， 且旋涡脱落频率会锁定在管道固有频率上，并在一定雷诺数范围内始终等于或接近管道固有频率，此现象称之为锁定或同步，此时管道运动振幅陡然增加，运动振幅之所以不会无限增大是因为有阻尼的存在，此阶段管道处于共振阶段，其运动振幅最大，涡激振动最为强烈；当雷诺数大于130时，旋涡脱落频率开始逐渐变大，此阶段脱离锁定阶段，进入解锁阶段；当雷诺数达到160时，管道会完全进入非锁定阶段，管道运动振幅会回到最初状态。

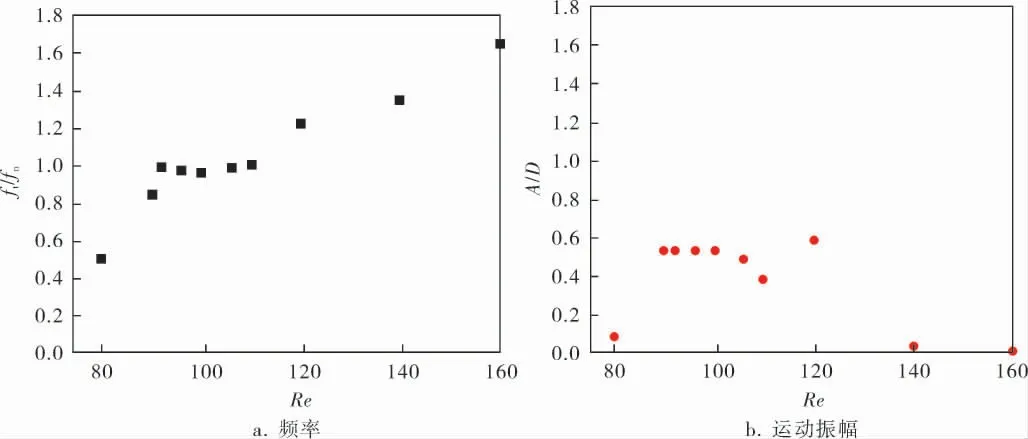
图2 不同雷诺数下管道频率和运动振幅的变化曲线

2.2 不同悬跨长度的管道流固耦合分析

对直径为0.3m， 悬跨长度分别为15、20、30、40、50、100m的管道建立流固耦合有限元模型，得到管道自振频率与悬跨长度的关系曲线如图3所示。 可以看出，管道悬跨长度相同时，阶数越高管道自振频率越大；同一阶数下，管道悬跨长度越大，自振频率越小；当悬跨长度超过40m时，通过与旋涡脱落频率计算范围比较发现， 前3阶管道自振频率与旋涡脱落频率有重合段，此时发生共振的可能性增大，应采取一定的措施避免发生共振现象。

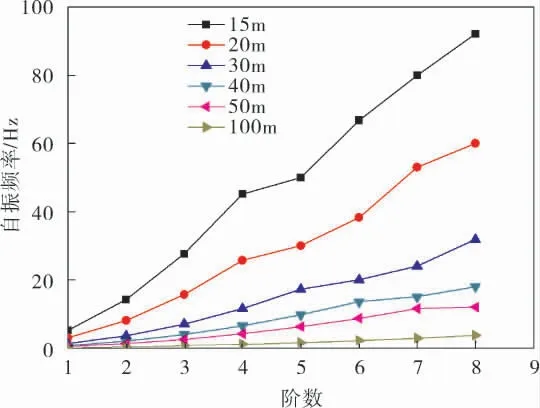
图3 管道自振频率与悬跨长度的关系曲线

2.3 不同管道直径的管道流固耦合分析

对悬跨长度为40m，直径分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8m的管道进行流固耦合分析，其自振频率与管道直径的关系曲线如图4所示。可以看出，管道直径相同时，自振频率随着阶数的升高而增大；同一阶数下，自振频率随着管道直径的增大而增大。对于直径为0.1～0.3m的管道，前3阶自振频率范围为0.288～1.960Hz； 对于直径为0.4～0.8m的管道，1阶自振频率范围为0.839～1.266Hz，与对应管道的旋涡脱落频率进行比较发现，这是管道发生共振的危险区域，此时应避免低阶共振的发生，适当增大管道直径也可以减小共振发生的概率。

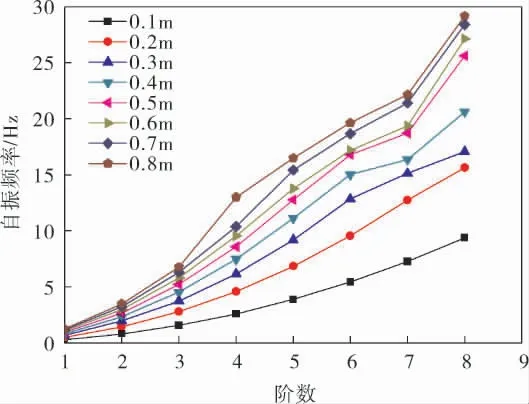
图4 管道自振频率与管道直径的关系曲线

3 结论

3.1 考虑流固耦合作用时的管道湿模态自振频率与不考虑流固耦合作用时的管道干模态自振频率相差较大， 数值之间可近似为两倍关系，因此必须考虑内外流体对管道振动的影响。

3.2 低雷诺数下，管道横向振动是引起涡激振动的主要原因。 随着雷诺数从80逐渐增大到160，管道从非锁定状态逐渐进入共振锁定再到解锁状态；当雷诺数为92时管道处于共振，此时升力和阻力系数急剧增大，管道横向振幅也达到最大值。

3.3 管道自振频率与悬跨长度成反比关系，悬跨长度越长其自振频率与激振频率接近范围越广。

3.4 管道自振频率随着管道直径的增大而增大，低阶为管道发生共振的危险区域。 对于以上现象，应采取相应的措施，避免共振的发生。