基于MATLAB Robotics Toolbox的四足机器人轨迹仿真与优化
陈明方,张凯翔,陈久朋,熊彬洲,李 奇,姚国一,李鹏宇
(昆明理工大学 机电工程学院,云南 昆明 650500)
近年来,仿生四足机器人成为了机器人领域关注的焦点之一。仿生四足机器人的结构特点使其相比于轮式、履带式机器人具有更好的对复杂环境和地形的适应性[1-2]。仿生四足机器人摆动相的末端轨迹决定着机器人的步幅大小和抬腿高度,对仿生四足机器人的稳定性和运动控制具有重要作用[3-5]。
目前,国内外学者对四足机器人末端轨迹进行了广泛的研究。美国波士顿动力公司“big dog”[6-7]以及意大利理工学院的“HyQ”[8]等产品都为其足端轨迹进行了详细的规划,使机体在运动过程中更加平稳,同时也减少了步态切换时的冲击性。日本Ibaraki大学的研究人员基于CPG调制对四足机器人的自主避障进行了步态研究和轨迹规划[9]。北京理工大学的研究人员也为其研究的四足机器人平台规划了足端零冲击轨迹[10]。但上述研究所使用的四足机器人平台大多采用液压驱动,若采用电机驱动方式,其轨迹规划对于四足机器人的各关节转动特性提出来更高的要求[11]。

本文针对电机驱动的仿生四足机器人,通过对Robotics Toolbox的二次开发,使其适用于具有3个关节的仿生四足机器人的单腿结构。文中对轨迹各中间点进行逆向运动学求解,得到各个角度中间点,再使用五次多项式曲线连接,使其各关节的转动特性符合参数要求。本研究针对机器人逆向运动学的多解问题进行优化,在Robotics Toolbox主程序中增加了角度选择优化算法,解决了关节转动的突变问题。对设定轨迹的实时仿真显示其各关节转动平稳柔顺。
1 仿生四足机器人运动学分析
1.1 建立D-H模型
以犬类动物的四肢模型为主要研究对象,通过对其解剖学模型进行深入分析,得出该类动物的通用性的结构特点。其中,总结得出犬类动物的四肢结构可以简化为3个关节的协同运动。即一个髋关节,可进行左右的侧摆运动;一个膝关节和一个踝关节可提供前后的运动变化。针对上述对象的结构特点,开发的具体实验平台如图1所示。同时,为了简化运算与轨迹仿真,将该实验平台抽象为如图2所示的关节模型,并建立各关节所对应的关节坐标系。
图中,{B}为基坐标系,{0}为单腿参考坐标系,{T}为足端坐标系。图中的各杆长度为l1=20 cm,l2=50 cm,l3=30 cm。
1.2 运动学分析
采用Denavit-Hartenberg(D-H)法对各关节坐标系和关节参数进行分析[17-18],可得足端坐标{T}在参考坐标系{0}中的齐次矩阵描述为
(1)
其中,X=l1·C1+l3·(C1·C2·C3-C1·S2·S3)+l2·C1·C2;Y=l1·S1+l3·(S1·C2·C3-S1·S2·S3)+l2·S1·C2;Z=l3·(C2·S3+S2·C3)+l2·S2。
式中,S1和C1分别表示sinθ1和cosθ2,其余各缩写式同理。通过足端在{0}系中的坐标描述,结合各杆件的长度参数,建立各关节角度与足端坐标的几何关系式
(2)
式中,S23和C23分别表示sin(θ2+θ3)和cos(θ2+θ3)。由式(2)的几何关系式可得单腿结构的运动学逆解
(3)
(4)
(5)
由上式中可以看出,相同的足端位置对应有两组不同的解,且呈对称关系,即姿态对称。由此可能产生运动学反解的多解问题,故需对其进行选择。
2 足端轨迹求解
2.1 应用工具箱求解
应用Robotics Toolbox中各类丰富的功能函数,可对机器人运动过程中的末端轨迹进行求解,通过求解的结果,对机器人的末端执行器进行轨迹规划与仿真。此方式进行轨迹规划的主要过程为:(1)通过末端位姿在参考坐标系中的矩阵描述,由反解函数得到对应的运动学逆解的各个关节角度值;(2)将初始关节角度与终点关节角度用关于时间的五次多项式曲线进行连接,得到如图3所示的关节角度变化曲线,其所对应的末端在三维空间中的实际运动曲线如图4所示。
2.2 连续轨迹曲线
由Robotics Toolbox生成的末端轨迹通常只有首末两个位置,中间用弧线连接。在实际使用过程中,往往需要在首末位置之间添加一系列中间点,使其末端按照规定的轨迹行走。因此文中以余弦曲线为例对其进行轨迹规划,即规定末端按照余弦曲线的轨迹行走,轨迹曲线的空间描述如下
(6)
通过在Robotics Toolbox的主程序中增加了循环算法,使其末端依次穿过各个中间点,连续地逼近设定的余弦曲线路径。设定的末端余弦曲线轨迹如图5所示。
在对上述的轨迹曲线仿真过程中,发现运行过程将出现关节角度突变的情况。如图6所示,展示了3个连续的关节角度中间点的运行情况。关节角在运行完后的瞬间如图6(a)所示,跳转到将近对称的位姿如图6(b)所示,之后又返回至原位姿附近,如图6(c)所示。在此过程中,将出现极大的角速度和角加速度突变状况。调出其反解函数ikine反解生成的部分角度数据,如表1所示,分析发现存在多解问题突变和周期性突变两种情况。

表1 由ikine函数生成的反解角度数据Table 1. Inverse angle generated by the ikine function
2.3 原因分析
对Robotics Toolbox的有关功能函数进行分析。由于其主要是针对6关节机器人所开发的,即基于末端有6个自由度时对应的位姿矩阵,通过反解函数ikine反解出其对应的关节角度。仿生四足机器人通常只有3个关节,即末端只有3个空间自由度。若由反解函数ikine反解存在一定缺陷,其反解出来的关节角度会出现若干点的周期突变。同时,反解函数ikine每次只反解出一组关节角度,存在角度选择的随机性,会由于多解问题的选择不当从而引起关节角度突变的情况[19]。因此,需对Robotics Toolbox进行二次开发,使其适应仿生四足机器人足端3个自由度的结构要求。
3 改进与优化
3.1 改进机器人工具箱
对反解函数ikine进行修改,即对该工具箱进行二次开发。将章节1中所求得的反解公式进行程序化,用其来替换ikine函数。将所求的角度值作为逆向运动学的关节角度值,代入上述循环算法的主程序中,针对表1中的运动轨迹点重新进行轨迹求解。由此得到角度数据,经分析后发现周期性突变情况得到改善。各关节角度数据如表2所示。

表2 改进反解函数后的关节角度数据Table 2. Joint angle after modifying the inverse solution function
从表中可以看出,关节角度值的周期性突变问题得到改善。同时,由于所求得的反解关节角度存在多解问题,若随机选择则会出现角度瞬时突变的情况(图7),其对应的角速度、角加速度会急剧增大,如图8和图9所示。
3.2 优化多解选择问题
由于存在逆向运动学的多解问题,若关节角度值选择不当,则相应关节在运动过程中的突变需要驱动系统产生极大的力矩来支撑其运动,这将对驱动元件造成损害。尤其是当采用电机驱动方式时,将产生极大的瞬时电流,对电机的运行过程造成较大冲击,从而影响电机的寿命。因此需要对多解问题进行优化,即选择合适的逆解角度值来避免角度突变问题的产生。优化方法采用最小角度变换为原则,将前一个运动状态的角度值作为基准,对下一个运动状态用逆向运动学公式反解,将求解出来的多组解与基准值进行求差值运算。差值运算所得到绝对值最小的一组解即作为下一个运动状态的关节角度值,代入到仿真运动的主程序中。如此循环,保证每次所得到的解都是角度变化最小的最优解。该过程可通过式(7)~式(8)进行求解
F=|θi(k+1)-θ(k)|
(7)
minF⟺θ(k+1)
(8)
本研究应用上述处理方法与优化原则,提出了一种优化算法用于运动学逆解的角度选择,并将其编为程序语言来实现上述处理过程。在运动仿真的主程序中加入该算法程序,利用该算法进行下一组关节角度值的优选。针对表1中的关节运动轨迹点重新进行优化计算与运动仿真,所得到优化后的关节角度值如表3所示。
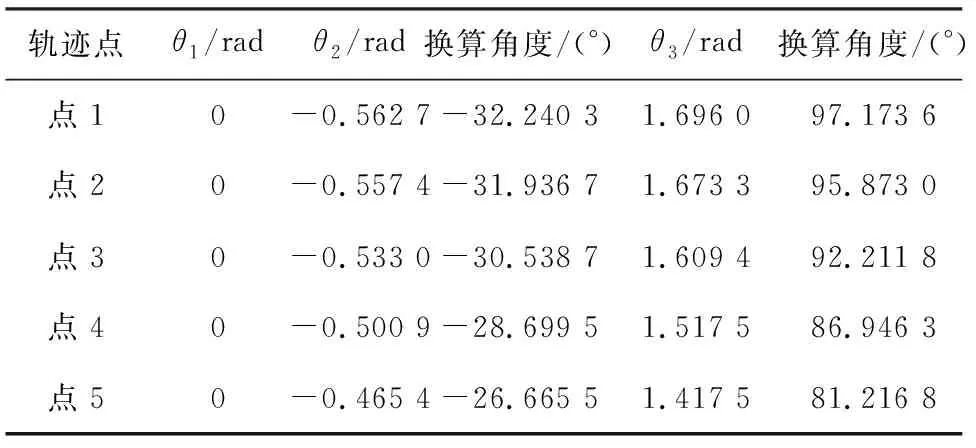
表3 优化后的关节角度数据Table 3. Optimized joint angle
由表3可看出上述轨迹点的突变问题得到改善,实现了最小的角度变化目标。同时,在对整个运动过程的仿真中显示:各个关节在沿设定轨迹运行过程中没有出现角度突变情况,如图10所示。整个过程对应的角度、角速度、角加速度曲线如图11~图13所示。角度特性曲线的结果显示,角度变化缓和,无明显突变,角速度、角加速度的最大值较小,在合理范围之内。
4 结束语
本文在建立仿生四足机器人运动学模型的基础上,对其正、逆向运动学进行了分析与求解。通过MATLAB Robotics Toolbox对简化模型进行仿真,发现有关节角度突变的情况存在。于是对 Robotics Toolbox底层函数进行研究与分析,得出如下结论:(1)角度突变是由于该工具箱内部的反解函数ikine的缺陷所致,其对四足机器人足端3个空间自由度结构的逆向运动学求解存在一些不适用性;(2)对求解轨迹的程序进行修改,用逆向运动学公式替代ikine函数,使其适用于3个自由度的足端结构,解决了原程序反解的周期性突变情况;(3)对逆向运动学求解的多解问题进行了优化,增加了角度选择优化算法,使其依据最小的角度变化原则进行关节角度的选择,可以解决由逆向运动学多解问题造成的角度突变情况。
本文通过对设定轨迹的实时动态仿真,显示其运动过程自然平缓,无突变情况,并分析了其角速度和角加速度特性曲线,发现其最大值在合理范围之内。本文的研究为基于Robotics Toolbox的实时轨迹规划研究提供了参考。

