永磁体助磁的单相双凸极电机优化设计
上官璇峰,马亚涛,王双平,胡刚强,李飞祥
(河南理工大学 电气工程与自动化学院,河南 焦作 454000)
家用电器对节能的要求越来越高,而其耗能主要集中在电机,这就需要制造更高效率的电机以达到家用电器日益提高的节能要求。家用电器常用电机为异步电机和永磁直流无刷电机。传统的异步电机虽然价格低廉,但效率较低,不能满足高效率要求。永磁直流无刷电机有较高效率,但是其永磁体位于转子表面,不适合高速运行,也容易发生不可逆退磁。定子永磁型双凸极电机的出现不仅满足了高效率要求,还解决了永磁体位于转子侧易发生不可逆退磁和不适合高速运行两方面问题[1-3]。近年来,国内外学者对定子永磁型双凸极电机进行了多方面的研究,取得了一系列研究成果,提出了很多理论方法,如磁力线划分法[4]、非线性磁网络法[5-6]、等效磁网络模型法[7]、磁热耦合法[8]等,并总结了一般定子永磁型电机的设计步骤[9]。该类电机调速控制系统与普通永磁电机相同,大多采用双闭环控制[10]。目前的研究主要集中在三相和多相,对于定子永磁型单相双凸极电机的研究比较少。文献[11]提出了一种具有非对称定子磁极的定子永磁型单相双凸极电机,在探讨工作原理的同时利用有限元仿真计算了其电磁性能。文献[12]提出了一种径向轴向双磁路的定子永磁型单相双凸极发电机,新结构的发电机拥有更高的功率密度。
本文研究的永磁体助磁的单相双凸极电机也是定子永磁型双凸极电机的一种,其永磁材料为铁氧体。文献[13]利用有限元软件仿真了该结构电机的空载特性,提出了两种不同的控制策略,但没有给出具体的设计步骤。本文将结合开关磁阻电机的设计原则给出该电机的具体设计步骤,并分析不同参数变化对电机效率和齿槽转矩的影响。最后以电机效率为优化目标,利用田口法[14-15]对电机进行优化。
1 电机结构与工作原理
1.1 电机结构
电机结构如图1所示,电机有2个定子极和4个转子极,其中每个定子极被中间隔磁槽分为左右2个半极。永磁体充磁方式为平行磁化,转子结构类似于磁阻电机。
1.2 工作原理
电机定转子极面之间采用锥形气隙,使电机转子静止位置相对均匀气隙情况下可偏转一定角度。当绕组通电后电枢磁场和永磁磁场之间相互作用产生转矩,电机开始起动,反电势第一次改变方向时电流也第一次换向,后续转子每转过45°机械角度电流换向一次,最终达到同步转速。
2 基本方程
2.1 电势方程
定子电路电压和磁链方程如下
(1)
其中,r为绕组电阻;is为绕组电流;e为反电势;ψ为磁链;ψpm为永磁体产生的磁链;L为绕组电感。
忽略电流对电感的影响,就等同于忽略了铁心饱和,反电势由下式表示
(2)
2.2 转矩方程
忽略铜耗和铁耗的情况下,电机电磁功率等于输入功率,电磁功率可以被推出
(3)
其中,Wf为电枢绕组电感储存的能量;Te为电磁转矩;ωr为电机转子旋转角速度。
由式(3)可得电机的电磁转矩
(4)
其中,Tr为磁阻转矩;Tm为永磁转矩。
2.3 功率方程
电机理想情况下永磁体产生的磁链,输入电压和电流如图2所示。
一个周期内的平均输入电功率可由下式表示
(5)
其中,T=θcr/ωr; ΔT=Δθ/ωr;θcr=2π/pr为转子极距角,Δθ=θ2-θ1=θ3-θ2为半个周期角度;pr为转子极数;ωr为转子角速度;t1~t3分别为转子位置θ1~θ3对应时刻
(6)
(7)
假设电机效率为η,则输出功率可由下式表示
(8)
电枢绕组端部电压Um可由电机空载反电势表示
Um=keE0
(9)
其中,ke为一个常数;E0为电机空载反电势。
因此,电机输出功率可由下式表示
(10)
空载反电势可由下式表示
(11)
其中,φ为空载情况下通过电枢绕组的磁通量;Nc为电枢绕组匝数;n为转子转速。
基于永磁磁链的线性模型,式(11)可以被进一步推导
(12)
电枢绕组最大磁通量为转子极与定子极左半极或右半极对齐时,可由下式表示
(13)
其中,kd为弱磁系数;αs为定子极弧系数;s为定子极距;le为轴向长度;Bδ为空载气隙磁密幅值。
因此式(12)可以被表示为
(14)
电流幅值由下式表示
(15)
其中,ki为一个常数;Irms为电流有效值;Dsi为定子内径;As为电负荷。
将式(14)、式(15)代入式(10)中得
(16)
由式(16)可得Dsi、le与输出功率之间的关系。
3 电机设计
电机初始设计要求如表1所示,电机结构参数图如图3所示。

表1 电机初始设计要求Table 1. Initial design requirement of the motor
由式(16)可得电机结构参数方程
(17)
一般情况下,kd、ke的取值在以下范围
kd=0.89~0.93
ke=1.3~2.0
(18)
取kd=0.9,ke=1.3,ki的取值与电机的控制方式、实际运行状况有关,假设ki=1.2。本文设计的电机额定功率为45 W,可参照小功率永磁电机电负荷的选取经验[14],取As=3 000 A·m-1。取电机空载气隙磁密Bδ=0.6 T。
将以上选取的参数值代入式(17)可得
(19)
电机定子内径与轴向长度的取值由电机细长比决定,细长比由下式表示
(20)
取细长比λ=0.5,则Dsi=42 mm,le=21 mm。
近似地认为转子外径与定子内径相等,根据开关磁阻电机的设计经验可得
(21)
取其比值为0.5,则Dso=84 mm。
永磁体助磁的单相双凸极电机有两个气隙。气隙g为定转子极齿表面之间的距离,称为第一气隙。气隙g1为定子极齿表面到转子槽底部的距离,较小的第一气隙可以得到更大的电磁转矩。但考虑到实际安装和加工工艺的限制,第一气隙不宜过小。参考相同容量的普通永磁电机和异步电机,可初步选取电机第一气隙g=0.4 mm。第二气隙参考开关磁阻电机的第二气隙选取方法,通常
g1=(20~30)g
(22)
取g1=23g=9.2 mm。
定子极隔磁槽宽度对电机整体运行性能有重要影响,过窄,则永磁体漏磁严重;过宽,则定子极齿铁心磁通密度过饱和,铁耗增大,空载气隙磁密减小,电机效率降低。因此,取定子极隔磁槽宽度c=4 mm。
转子轭部h2应保证轭部铁心在电机正常运行时最大磁通密度不过饱和,故轭部高度取值范围可表示为
(23)
其中,bpr为转子极齿宽度,初步取h2=7 mm。
电机轴径Di选择时不能过小,过小的轴径不能满足对机械强度的要求,而且还会造成电机噪声的增加,转子振动和偏心。
Di>=Dsi-2g1-2h2≈10 mm
(24)
定子左右轭部宽度
(25)
其中,bps为定子极齿宽度。
定子极上部和下部轭铁高度为h1,该部分为主磁路,应保证该部分铁心在电机正常工作时不过饱和,故初步选取h1=8 mm。
选择牌号为AC-7的铁氧体作为永磁材料,在20 ℃环境温度下,永磁体退磁特性近似为线性,如图4所示。
永磁体工作点的剩磁BM、磁场强度HM分别表示为
(26)
(27)
其中,Br和Hc分别为永磁体的剩余磁通密度和矫顽力,通过安培定律可得
HMd=Hδg
(28)
其中,Hδ为气隙磁场强度;d为永磁体磁化高度,从而可得
(29)
通常情况下BM/Br的取值范围在0.7~0.9之间,本文选择的永磁体剩磁Br=0.33 T,矫顽力Hc为260 000 A·m-1。
然后,将Bδ=0.6 T,Br=0.33 T,BM/Br=0.85,g=0.000 4 m,Hc=260 000 A·m-1代入式(29)可得到d≈4.8 mm。
由于电机的特殊结构,因此初步取磁桥宽度w2=0.5 mm,当电机定子极隔磁槽和磁桥宽度确定后,永磁体宽度可由下式计算
wpm>=0.5(Dso-c-4w2)=39 mm
(30)
为了实现电机的自起动,定转子极面之间采用锥形气隙(渐变型气隙),定转子极面之间最小气隙为前文设计的气隙g。气隙形状如图5所示。
这里定义定转子极面之间最大气隙与最小气隙比率为a
(31)
a的取值大小直接影响电机的整体性能,a过小则电机起动能力差、起动时间长、甚至不能正常起动;a过大,则电机的齿槽转矩峰值和气隙磁阻增大。虽然电机的起动能力得到提高,但效率会降低,转矩及转速波动增大。故初步选取a=1.5。
电机的最终主要设计参数如表2所示。
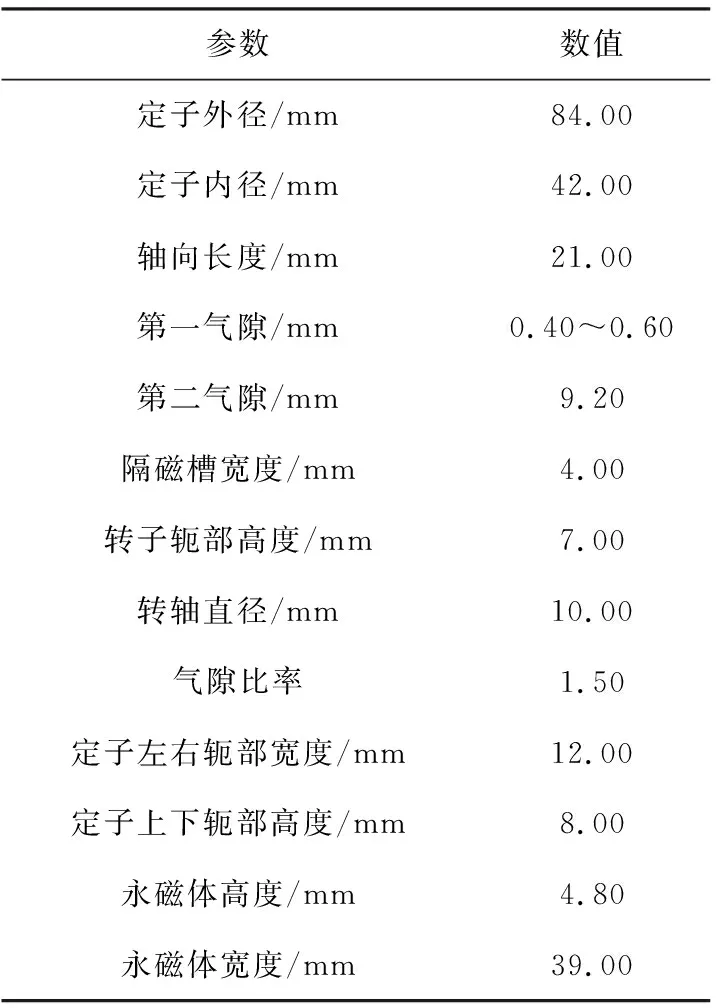
表2 电机主要设计参数Table 2. Main design parameters of the motor
4 电机参数对电机稳态性能的影响
对于本文设计的永磁体助磁单相双凸极电机,电机效率为重要的性能指标之一。此外,单相电机的起动能力也是需要考虑的性能指标。在起动过程中正向的齿槽转矩有助于电机起动,负向的齿槽转矩会降低电机的起动能力,所以分析不同电机参数值对电机效率和齿槽转矩正负峰值代数和的影响,对于选择合适的电机参数值至关重要。
4.1 定转子极弧配合对电机效率和齿槽转矩的影响
不改变电机其它参数的情况下,不同定转子极弧配合时一个周期内的齿槽转矩如图6所示。不同定转子极弧配合时电机效率和齿槽转矩正负峰值代数和如图7所示。
通过有限元分析,定子极弧小于90°时,电机齿槽转矩在一个周期内的形状与图6中曲线1近似,即在一个周期内出现第二个较大的正向峰值。当定子极弧大于等于90°时,电机齿槽转矩在一个周期内的形状与图6中曲线2近似。一个周期内有第二个较大正向峰值时,无法确定电机停止工作时转子的最终静止位置,对电机的下次起动造成影响,同时也会增大电机的转矩波动。
由图7(a)可以看出,不同定转子极弧配合下,定转子极弧配合为(80°,40°)、(100°,40°)时齿槽转矩正负峰值代数和分别为最大、最小值。定子极弧超过90°时,齿槽转矩正负峰值代数和会迅速减小,与转子极弧取值无关,不利于电机起动。但过大的齿槽转矩正负峰值代数和对于电机的稳态运行不利,会增大电机的转矩波动。因此,在满足电机起动要求的前提下,尽量选择齿槽转矩正负峰值代数和小的定转子极弧配合。
由图7(b)可知定转子极弧配合为(80°,35°)、(100°,50°)时电机效率分别为最高和最低。转子极弧为30°和35°时,随着定子极弧的增加,电机效率都逐渐降低。转子极弧为40°、45°、50°时,定子极弧从80°~85°变化时电机效率逐渐升高,都在85°时达到最大值,定子极弧继续增加,效率都逐渐降低。转子极弧为50°时,无论定子极弧取多大值。由于转子体积增加过多,电机转动惯量变大,铁耗升高,使电机效率始终低于其它定转子极弧配合。
4.2 轴向长度对电机效率和齿槽转矩正负峰值代数和的影响
不改变电机其它参数的情况下,不同轴向长度对效率和齿槽转矩正负峰值代数和的影响如图8所示。由图8可知随着电机轴向长度的增加,电机体积增大,在相同的电枢电流下,电机输出转矩增加。在保证电机相同输出功率和转速情况下,电机效率随着轴向长度的增加不断提高,齿槽转矩正负峰值代数和也随着轴向长度的增加不断增大。
4.3 气隙比率对电机效率和齿槽转矩正负峰值代数和的影响
不改变电机其它参数的情况下,不同气隙比率对效率和齿槽转矩正负峰值代数和的影响如图9所示。
随着气隙比率的增加,定转子极面间气隙磁阻增大,在保证电机额定运行工况下,电枢电流升高,电枢绕组铜耗增加。电枢电流的升高使绕组产生磁通量增加,定转子铁心磁密升高,铁心局部饱和程度增加,铁耗增大,电机效率降低,齿槽转矩正负峰值代数和随着气隙比率的增加逐渐增大。
4.4 隔磁槽宽度对电机效率和齿槽转矩正负峰值代数和的影响
不改变电机其它参数的情况下,不同隔磁槽宽度对效率和齿槽转矩正负峰值代数和的影响如图10所示。
由图10可知,随着隔磁槽宽度的增加,永磁体极间漏磁逐渐减小,电机效率提高。当隔磁槽宽度为4.5 mm时效率达到最高,永磁体极间漏磁降至最低。如果隔磁槽宽度继续增加,将导致定子极齿铁心饱和,铁耗增加,电机效率降低。齿槽转矩正负峰值代数和随着隔磁槽宽度的增加而不断增大。
4.5 永磁体磁化高度对电机效率和齿槽转矩正负峰值代数和的影响
不改变电机其它参数的情况下,不同永磁体磁化高度对效率和齿槽转矩正负峰值代数和的影响如图11所示。
由图11可知,随着永磁体磁化高度的增加,永磁体产生的磁通不断增加,电机效率提高,当永磁体磁化高度增加到5.4 mm时,定子极齿铁心接近饱和,电机效率达到最高。若继续增加永磁体磁化高度,则铁心饱和程度升高,绕组磁通量不再增加,铁耗增大,电机效率不断降低,齿槽转矩正负峰值代数和随着永磁体磁化高度的增加不断增大。
5 基于田口法的电机优化
对于本文研究的永磁体助磁的单相双凸极电机,在保证电机正常起动情况下,电机的效率是最为关心的性能指标,所以将电机效率作为优化目标。根据前一章节的分析,随着电机轴向长度的增加电机效率逐渐升高,但过大的轴向长度将使电机功率密度降低、制造成本增加、齿槽转矩正负峰值过大,故将轴向长度定为30 mm。定子极弧小于90°时不利于电机的起动,大于90°时电机效率下降明显,故将定子极弧定为90°。最后将气隙比率a、转子极弧b、隔磁槽宽度c、永磁体磁化高度d作为优化参数,其中气隙比率a为2水平,其余参数为3水平,具体参数和水平值如表3所示。
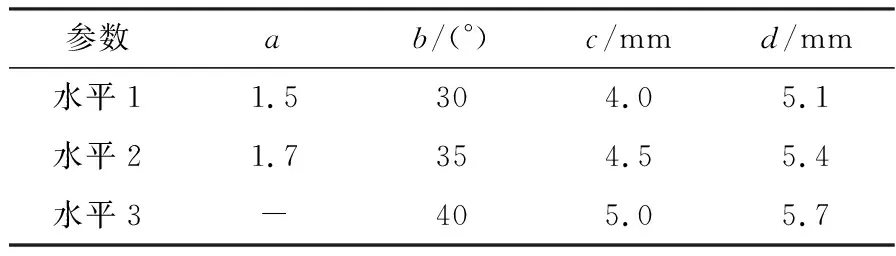
表3 电机优化参数取值范围Table 3. Range of motor optimization parameters
由表3的参数进行全部实验,共需要2×34=162实验次数,而采用田口法进行正交实验,则只需要18次实验分析,节省了大量的时间。实验正交表及有限元分析结果如表4所示。

表4 正交矩阵及有限元分析结果Table 4. Orthogonal matrix and results of finite element analysis
为了分析各优化参数对电机效率的影响,求解出每个参数每个水平下的平均值,例如转子极弧b在水平1下的电机效率平均值,计算式如下
(32)
式中,ηb1为某个参数某个水平下效率的平均值;η(n)为包含该水平的实验结果。相同方法求解其它参数不同水平平均值如表5所示。

表5 各参数每个水平电机效率平均值Table 5. Average of the efficiency of the motor at each level of different parameters
对表5的数据进行整理,得到电机各参数不同水平值下效率平均值,如图12所示。
进一步应用方差分析法对各参数变化对电机效率影响所占的比重进行分析。比重用SS表示,计算式如下
(33)
其中,xi为优化参数;S为电机效率;mxi(Si)为表5中x的第i个水平下电机效率S的平均值;m(S)为表4中S的平均值。最终计算结果如表6所示。

表6 各参数对电机效率影响所占比重Table 6. Proportion of the influence of each parameter on the efficiency of the motor
由表6可知,隔磁槽宽度对电机效率影响最大,其次为永磁体磁化高度,对电机效率影响最小的为气隙比率。由表4可知,实验8电机效率最高。故最优的电机参数组合为气隙比率1.5、转子极弧40°、隔磁槽宽度4.5 mm、永磁体磁化高度5.7 mm。优化后电机效率为89.86%,相比优化前的85.40%提高了4.46%。
6 结束语
本文推导了永磁体助磁的单相双凸极电机在理想运行工况下的基本方程,利用推导的功率方程结合开关磁阻电机的设计原则设计出一台额定功率45 W,额定转速2 000 r·min-1的永磁体助磁的单相双凸极电机。然后分析了不同定转子极弧配合、气隙比率、轴向长度、隔磁槽宽度、永磁体磁化高度对电机效率和齿槽转矩正负峰值代数和的影响,为电机的优化提供了参考。最后以电机效率为优化目标,利用田口实验设计方法对电机进行了优化。优化后电机效率为89.86%,相比优化前提高了4.46%。各优化参数中对电机效率影响所占比重最大的为隔磁槽宽度,其次为永磁体磁化高度,最小为气隙比率。
总结出的设计流程对该类型电机的设计具有一定的参考价值。但在本文设计中假设了一些理想情况,后续还需根据实际应用情况对设计流程进一步补充和完善。

