探究非自治—捕食者-两互惠食饵模型的动力学行为
新疆建设职业技术学院 李 艳
“我们要建设的现代化是人与自然和谐共生的现代化。”当前,在绿色发展理念下,全球都大力倡导节能减排,希望能推进全球环境的治理,实现人与自然和谐共生。而要想实现这一目的,首先必须加强生态研究,推动形成人与自然和谐发展的现代化建设新格局。在生态学中,最受人们关注的问题就是物种多样性问题,而在物种多样性问题中,物种的共存以及持续性生存问题是其重要的组成部分。目前,随着人们对地球生物圈开发力度的加大,很多物种逐渐成为濒危物种,甚至一部分永久消失了,为了保持地球生物物种的多样化,实现人与自然的和谐共生,研究非自治—捕食者-两互惠食饵模型的动力学行为就变得十分重要且十分紧迫。
一、数学生态学简析
数学生态学是一门研究数学与生物学的交叉学科,这一学科是借助数学相关的知识、理论和方法去描述、分析并解释自然生态环境中的一些生态现象、生态问题,从而探索出相应的生物学问题。在该学科的研究中,探索的方式方法有很多种,但目前最常用的就是借助数学知识、理论和方法构建相应的生态模型,把原本复杂的生物种群关系转化为数学模型,然后借助相应的数学知识和理论对其动力学行为进行分析。通过这样的研究,能有效促进生态学理论的顺利发展,对于当前构建人与自然和谐共生的生态系统具有广泛的实际应用价值。
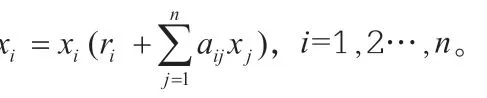
这一模型可以描述出不同物种种群之间的三种生存关系:一是竞争关系,如农作物和杂草争夺阳光和养分;二是捕食食饵关系,如非洲大草原上狮子、猎豹等捕食角马;三是互惠互存关系,如犀牛和犀牛鸟、蚂蚁和蚜虫、寄居蟹和海螺等。Lotka-Volterra 模型的提出吸引了全球众多的数学家和生物学家,很多学者在这一模型的基础上进行了进一步研究并对相关理论进行了改进,延伸出了众多的生物数学模型。在实际的生态环境中,不同物种之间的生存关系并不是单一存在的,而是同时存在着更为复杂的关系,即不同物种之间的生存关系是一种复杂多变的关系,可能同时存在着两种或三种生存关系。要想建立确定性的模型来解决生物学中的问题,应该运用大数定律,从而建立比较稳定状态的数学模型。而本文探究的就是一种捕食者捕食两种存在着互惠互存关系的食饵。其模型如下:
模型中的xi(t)代表的是在t时刻食饵种群的密度值;y(t)则是在t时刻捕食者种群的密度值;而其他系数a1(t)、b1(t)、c1(t)、d1(t)、D1(t)、e(t)、f(t)(i=1,2,t≥0)都是连续、有界、严格正的函数。为了更好地探究其生物学意义,研究其动力学行为,运用微分方程对其原理和构造进行系统讨论。其中,文章涉及的符号代表意义见表1。
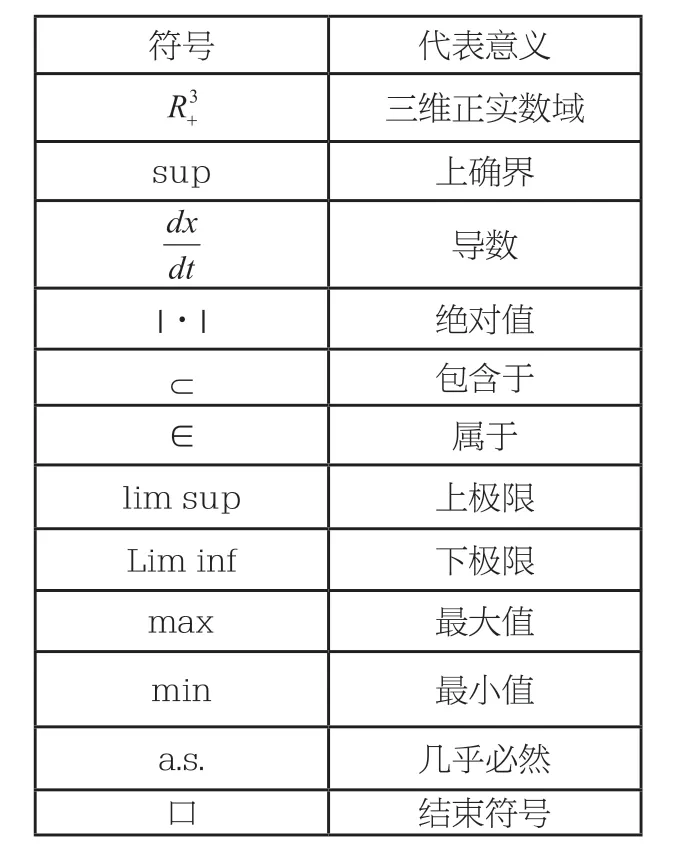
表1:文章涉及的数学符号说明
二、非自治—捕食者-两互惠食饵模型的动力学行为分析
是本系统的正不变集。当xi(t0)>0 时,则xi(t)>0,y(t)>0(i=1,2),因此,本系统满足正初值的就能够保持恒正。所以集合R 是本系统的正不变集。如果本生态系统中始终存在着一个紧区域D ∈Int ,使得本系统的任何满足正初始值条件(1,2)的解(xi(t),x2(t),y(t))都能最终进入并保留在紧区域D内,这样本系统就能保持一致持久性。
综上所述,非自治—捕食者-两互惠食饵模型的动力学行为在自然界中十分普遍,本文就对这种模型在理性状态下的持续性和正解全局渐进稳定性进行了探讨,可能还存在一定的不足,但希望能为相关人士的进一步深入研究提供参考。

