Delayed SubHopf-Fold/Fold Cycle簇发振荡及其动力学转迁

张 真 真

(江苏大学京江学院，212013，江苏，镇江)

0 引言

多尺度的耦合效应，广泛存在于工程实际中，如化工系统BZ反应中反应物的消耗速率不同[1]、旋转机械中存在低频周期激励或参数激励与系统自然频率的耦合[2]、神经系统中的簇放电现象[3]和生物系统中捕食-食饵模型[4]等。多尺度系统的响应中往往会出现大振幅振荡与小振幅振荡的交替，这种现象叫做簇发振荡或者混合模式振荡[5]。通常，大振幅振荡表现为轨迹在大振幅极限环向量场中的运动[6]，这种运动形式可以称为激发态运动。小振幅振荡表现为轨迹在平衡点吸引域或小振幅极限环向量场内的运动[7]，这种运动形式叫做沉寂态运动。在激发态和沉寂态交替转迁过程中，一般存在2种重要的分岔形式[8]，一种分岔使得系统由激发态进入沉寂态，另一种分岔使得系统由沉寂态进入激发态。基于这2种分岔形式，Izhkevich[9]提出了一种较为直观且被广泛接受的簇发振荡分类方法。

根据多尺度系统数学模型中耦合形式的不同，多尺度系统通常可以分为3类：第1种是时域上的耦合，无量纲模型表现为系统受到小参数扰动；第2种是频域上的耦合，数学模型表现为系统存在不同变化频率的相互作用；第3种是时域和频域的组合，模型上表现为小参数扰动和不同变化频率的耦合。低频外激或参激作用下的非线性系统是一类典型的频域多尺度系统，具有广泛的科学和工程背景[10-12]，引起了国内外学者的广泛关注，尤其是针对簇发振荡的研究。如陈章耀[13]等人研究了周期激励作用下广义Chua电路的簇发振荡现象，给出了两类典型对称周期簇发的动力学机制。韩青爽[14]等人分析了周期激励作用下水轮机调节系统的簇发振荡行为，并给出了簇发行为随激励振幅的动力学演化。侯静玉[15]等人给出了周期激励作用下分数阶Belousov-Zhabotinsky化学反应的稳定性和快慢行为机理。Simo和Woafo[16]揭示了双势阱Duffing振子在外周期强迫激励下的簇发振荡行为。Kovacic and Lenci[17]发现一类纯非线性振荡器在低角激励作用下，系统响应表现为簇发振荡，这种振荡是由慢流行附近的快速振荡引起的。

目前的研究大都是针对余维-1分岔展开的，并且Izhkevich[9]已经给出了低维光滑系统与余维-1分岔相关的所有簇发类型，但对于分岔滞后(慢通过效应)等特殊行为诱发的簇发行为成果较少。分岔滞后最早见于Baer[18]等的工作，他们发现如果控制参数为线性时变参数，当控制参数变化穿越超临界Hopf分岔点时，系统轨迹不会立刻从稳定平衡点的吸引域进入稳定极限环的向量场，而是仍然沿着平衡点继续运动一段时间，然后才进入稳定极限环，这种现象就称为分岔滞后，或者称为记忆效应或慢通过效应。分岔滞后可以产生非常有趣的簇发振荡类型，如马新东[19]等研究了一类由叉形分岔(pitchfork分岔)滞后诱发的混沌簇发行为；韩修静[20]等发现了一种由叉形分岔滞后和边界危机共同作用引起的混沌簇发振荡。以上成果的研究对象都是参数激励，对于系统受外部周期激励的情况很少涉及，或者就用慢通过效应代替，没有深入研究。本文针对改进型van der Pol-Duffing系统在低频激励下的一类由Hopf分岔滞后引起的簇发振荡，应用稳定性和分岔理论，结合数值模拟和快慢分析法，揭示了该簇发行为的产生机理及随控制参数变化的动力学演化。周期激励下的van der Pol-Duffing系统的数学表达式是

(1)

式中：参数a>0，b>0，c>0，d是任意实数，f是激励振幅，ω为激励频率且满足0<ω≪1，即外激励频率与系统自然频率ω0之间存在量级差异。由于0<ω≪1，在周期T内，激励fcosωt变化非常缓慢，因此可将fcosωt视为慢变参数δ，方程(1)转化为广义自治方程

(2)

本文旨在探讨周期激励下系统的不同簇发振荡形式。重点是研究一类由Hopf分岔滞后诱发的簇发振荡产生机制。本文的组织结构如下，在第1节中，给出了方程(2)的平衡点及其稳定性，分析了平衡点的分岔类型及其临界条件；第2节通过选择合适的参数，应用转换相图和分岔图的叠加等手段，揭示了由亚临界Hopf分岔滞后诱发的簇发振荡机理；第3节研究了激励振幅和频率对系统动力学行为的影响，给出了分岔滞后簇发行为随参数变化的动力学演化；最后，总结全文。

1 系统的平衡点及其稳定性

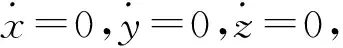
另一方面，在平衡点E0(x0,0,x0)处对系统进行线性化，可以得到雅克比矩阵

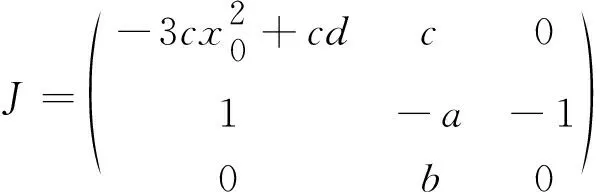
(3)

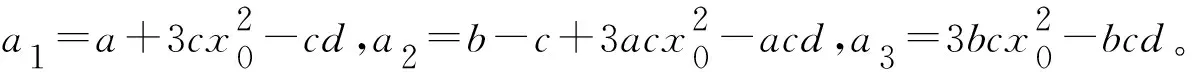
Fold分岔：当a3=0时，方程(2)的3个平衡点退化为一个平衡点，并且特征方程出现零根，这表明系统会出现fold分岔，响应在不同平衡点吸引域之间切换时有跳跃现象产生。

以参数c=10，d=0.1，a=2，b=9，f=2，ω=0.005为例，系统关于δ=2cos0.005t的单参数分岔图见图1所示。当δLPC2=-0.456<δ<δLPC1=0.456时，存在稳定的同宿极限环LC1，LC1和不稳定的极限环LC2和LC3在极限环的fold分岔点LPC1和LPC2处碰撞消失，在分岔的两侧只存在稳定的平衡点E+和E-。稳定的平衡点E+和E-经由亚临界Hopf分岔subH1和subH2(δsubH1,2=±0.167)失稳。轨迹在2个fold分岔点LP1和LP2(δLP1,2=±0.125)处产生跳跃现象。

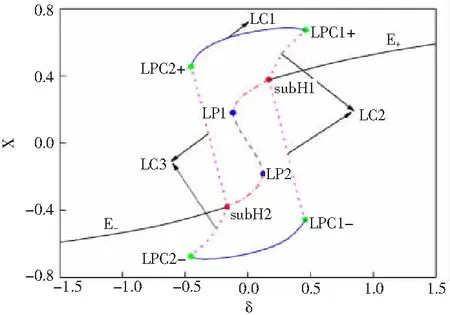
subH1、subH2表示亚临界Hopf分岔；LPC1(+,-)和LPC2(+,-)表示极限环的fold分岔；LP1、LP2表示fold分岔；实线表示稳定的极限环LC1；虚线表示不稳定的极限环LC2和LC3；点划线表示不稳定的平衡点；划线表示鞍点

2 Delayed subHopf-fold/fold cycle簇发振荡

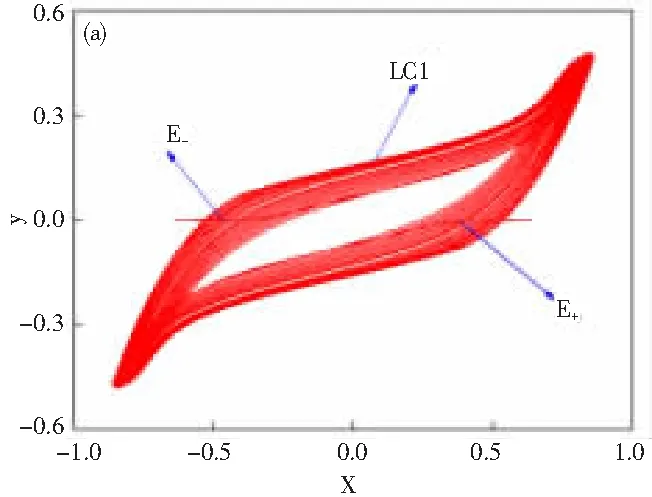
基于c=10，d=0.1，a=2，b=9，f=2，ω=0.005时的系统稳定性和分岔，下面讨论在该组参数条件下的簇发振荡行为，对应的相图和时间历程如图2所示。很明显，系统轨迹在2个平衡点和2个极限环之间转换。

(a)相图

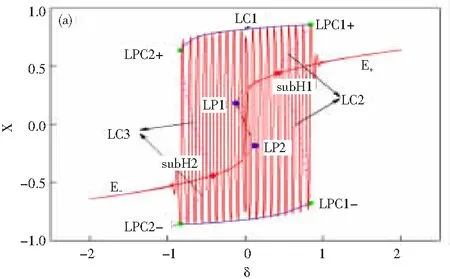
这种动力学行为的产生机制可以通过将转换相图叠加到分岔图上进行分析，如图3所示。假设系统轨迹从慢变量δ的最大值2开始出发，此时系统处在稳定平衡点E+的吸引域内，表现为沉积态运动。当δ减小至δ=0.167时， 亚临界Hopf分岔subH1出现，稳定平衡点E+失稳，但从图3可以看到，系统轨迹并没有立刻转到稳定极限环E+的向量场中运动，而是继续沿着不稳定平衡点E+运动一段时间，这就是由亚临界Hopf分岔滞后导致的。当δ减小到δ=0.167时，分岔滞后消失，同时可以看到fold分岔LP1出现，LP1使轨迹跃迁到下支上运动，分岔滞后点出现使得轨迹进入稳定极限环LC1中运动，对应着激发态运动。然后轨迹一直处在激发态运动中，直到LPC2出现，使得稳定极限环LC1和不稳定极限环LC3碰撞消失，此时稳定的吸引子只剩下平衡点E-，轨迹就沿着平衡点E-运动直到δ减小至其最小值-2，完成半个周期运动。另外半个周期运动与前半个周期运动类似，这里不再赘述。

图3 分岔图与转换相图的叠加

这里出现了一个非常有趣的现象，就是在fold分岔点LP1或LP2出现的时候，亚临界分岔滞后点subH1和subH2也同时出现，这就是使得轨迹在上支和下支之间跳跃的同时，也使轨迹进入稳定极限环。这表明在fold分岔点LP1或LP2处，存在2种分岔形式，一种是fold分岔，另一种是分岔滞后。以往的研究只是考虑了分岔滞后会产生在不同的参数区域，对应不同的簇发振荡模式，而本文的研究表明分岔滞后可以与另一种分岔同时出现，即余维-2分岔。所以根据Izhikevich对簇发的分类方法，这种簇发类型可以定义为delayed subHopf-fold/fold cycle簇发振荡。delayed subHopf-fold表示这2种分岔出现在同一点，且在这一点处激发态运动开始，fold cycle表示激发态运动结束于极限环的fold分岔(LPC分岔)。

3 delayed subHopf-fold/fold cycle簇发振荡的动力学转迁

上面给出了delayed subHopf-fold/fold cycle簇发行为的产生机制，下面研究这种簇发振荡随参数变化的动力学转迁机制。

3.1 两参数分岔图

图4给出了当c=10，d=0.1，a=2，b=9，ω=0.005时，系统关于参数b和δ的两参数分岔图。整个参数平面可以分为7个部分，其中左右两部分关于区域4是对称的。

在区域1和区域7内，存在稳定的平衡点E+和E-。当参数穿越极限环的fold分岔曲线LPC1和LPC2进入区域2和6后，E+和E-继续保持稳定，同时在2和6内存在2个稳定的极限环，因此区域2和6是双稳态区域。当参数穿越亚临界Hopf分岔曲线subHopf1和subHopf2进入区域3和5后，E+和E-失稳，变为不稳定的平衡点，此时区域3和5内的稳定吸引子是2个稳定的极限环。当参数变化穿越fold分岔曲线Fold1和Fold2后，2个稳定的极限环继续存在，同时4区域出现不稳定的鞍点。

图4 两参数分岔图

图5 不同动力学行为对应的区域

根据分岔曲线穿越区域和亚临界Hopf分岔曲线与fold分岔曲线距离的不同，大致可以将整个区域分为3个部分，如图5所示。在区域C处，系统的动力学行为主要受到2个fold分岔的影响。在区域B处，由于fold分岔曲线和亚临界Hopf分岔曲线距离很近，fold-subHopf余维-2分岔出现，系统的动力学行为表现为delayed subHopf-fold/fold cycle簇发振荡。在区域A内，fold分岔曲线和亚临界Hopf分岔曲线距离较远，不会出现fold-subHopf余维-2分岔，系统的动力学行为与余维-1分岔有关。

delayed subHopf-fold/fold cycle簇发振荡是区域B中的典型动力学现象，它随参数b的变化有2个转迁方向，一是由B进入A，另一种是由B进入C。下面分别讨论这2种情况对应的动力学转迁。

3.2 delayed subHopf/fold cycle簇发振荡

区域A内参数b的取值不会影响动力学行为的本质特性，因此选择参数b=1为例，系统的动力学行为如图6所示，轨迹同样在2个稳定平衡点和稳定极限环之间转迁。

这种动力学行为的动力学机制仍然可以通过分岔图和转换相图的叠加进行揭示，如图7所示。假设轨迹仍然从δ的最大值2对应的位置开始往右运动，此时稳定的吸引子是E+，因此轨迹沿着E+的向量场以近乎直线的方式运动到点subH1。在点subH1处亚临界Hopf分岔出现，E+失稳，从图7(b)中清楚地发现，轨迹仍然沿着不稳定E+运动了一段时间，然后才转到稳定极限环LC1中运动，这仍是分岔滞后引起的。当分岔滞后点出现后，轨迹在LC1中很自然地从上支运动到了下支，没有经过fold分岔点LP1。当δ减小到δsubH2时，不稳定的平衡点E-变得稳定，同时产生一个不稳定的极限环LC3，但此时轨迹仍处在LC1中。随着δ减小到δLPC2，稳定的极限环LC1和不稳定的极限环LC3碰撞消失，此时稳定的吸引子只剩下E-，轨迹也就转到E-的吸引域内运动，直至δ减小到其最小值-2，完成半个周期运动，另外半个周期运动与前面的分析一致。

(a) (x,y)平面内的相图

(a)分岔图与转换相图的叠加

这种簇发模式可以定义为“delayed subHopf/fold cycle”簇发振荡。因为激发态运动开始于亚临界Hopf分岔滞后，结束于极限环的fold分岔。分岔图中虽然有fold分岔LP1和LP2，但轨迹没有通过这2个fold分岔点在上支和下支之间转换。

3.3 fold/fold簇发振荡

当参数b=12时，系统的相图和时间历程如图8所示，可以发现系统轨迹是在2个稳定平衡点之间转迁的。

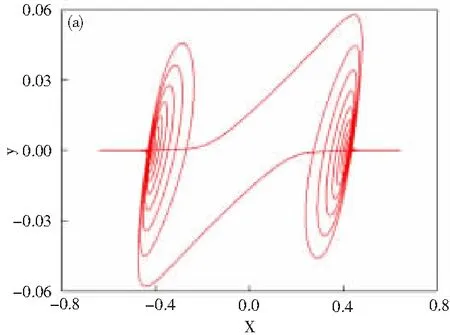
(a)相图

这种动力学行为的产生机制可以通过图9所示的叠加图进行揭示。仍假设轨迹从δ的最大值2处开始运动，此时的稳定吸引子是E+，轨迹就沿着E+的向量场作光滑曲线运动直到fold分岔点LP1产生。LP1使轨迹从上支跳跃到下支运动，伴随着振幅逐渐减小的高频振荡，之后轨迹趋近于稳定平衡点E-的向量场对应的平滑曲线，直到δ的最小值-2。

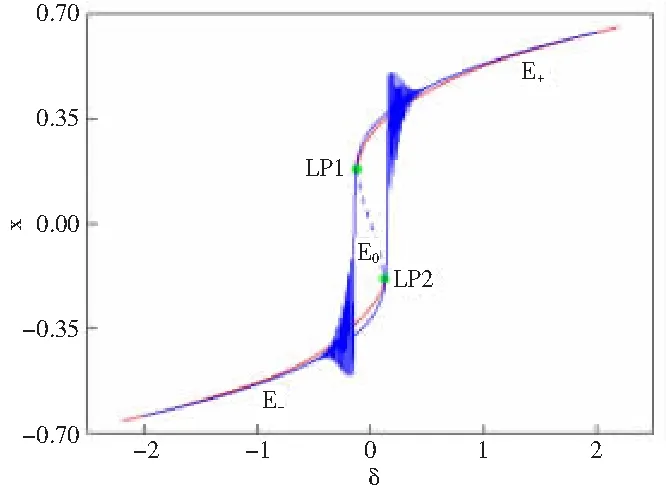
图9 b=12时分岔图与转换相图的叠加

由于轨迹是通过2个fold分岔点在2个稳定平衡点E+和E-之间切换的，激发态运动对应的是从上支跳跃到下支或下支跳跃到上支时的振幅逐渐减小的高频振荡，因此这种簇发模式称为“fold/fold”簇发振荡或者“fold/fold”滞后环，这是一种非常常见的簇发形式。

4 结论

研究了低频周期激励下van der Pol-Duffing系统的簇发动力学行为，揭示了分岔滞后在簇发行为中的作用以及一类由Hopf分岔滞后诱发的余维-2簇发振荡的产生机制，即delayed subHopf-fold/fold cycle簇发振荡。研究表明，亚临界Hopf分岔滞后使系统出现余维-2分岔的特征，即在fold分岔出现的时候，分岔滞后点同时出现，这就使得轨迹产生跳跃现象的时候，同时进入稳定极限环吸引域运动。这种现象可以用(δ,b)双参数分岔图清晰揭示，在fold分岔出现的时候，在该点邻域内亚临界Hopf分岔产生。此外，探讨了delayed subHopf-fold/fold cycle簇发振荡随参数b变化的动力学转迁机制。研究表明，随着b减小，亚临界Hopf分岔滞后点不会与fold分岔同时出现，系统的动力学行为表现为delayed subHopf/fold cycle簇发振荡。随着b增大，亚临界Hopf分岔滞后现象不再出现，系统的行为只与fold分岔有关，即fold/fold簇发振荡。