柱形和E形钢阻尼装置比较及试验分析

高 昊 王君杰 王剑明

（1.同济大学桥梁工程系，上海200092；2.成都济通路桥科技有限公司，成都611430）

0 引 言

金属阻尼器工作性能稳定、后期维护费用低、可预期性强，近年来在国内外的桥梁工程中得到了广泛应用［1］。国外，Vasseghi［2］提出采用 X 形钢板代替桥梁上的传统混凝土挡块，推广了X 形加劲阻尼装置在桥梁结构中的应用。Tsai［3］采用三角形钢板作为加劲阻尼装置，结合工程案例介绍了在工程抗震应用中的设计方法。Tyler［4］建议在建筑和桥梁结构中使用锥形的悬臂板或悬臂柱，并开展了拟静力试验进行验证。Arcangeli［5］创新性地采用“E”字形钢材制作阻尼装置，设计了一系列的拟静力和振动台试验。Jelena［6］讨论了桥梁工程用“C”字形和“S”字形等钢阻尼装置的耗能能力。国内，李建中等［7-8］提出了X 形软钢阻尼挡块配合板式橡胶支座的准隔震系统，在四川雅沪高速公路中的桥梁中得到使用。叶爱君等［9-10］将三角形钢板和球型钢支座结合在一起，提出了大跨度斜拉桥横向减震体系及设计方法。王君杰等［11-12］发明了可滑移柱形软钢阻尼装置，并在国内斜拉桥和连续梁桥中进行了探索性应用。管仲国等［13-14］将E形钢阻尼支座用于大跨度自锚式悬索桥的横向减震设计。徐艳等［15］采用“C”字形钢阻尼装置代替传统混凝土挡块提高中等跨径斜拉桥横桥向抗震性能。

其中，采用钢阻尼装置实现单向震动控制在中小跨度梁式桥顺向和横向、大跨度桥梁横向比较常见。图1（a）为柱形钢阻尼装置在广东榕江大桥（斜拉桥）主塔处提供横向阻尼力的案例［16］，图1（b）为南京江心洲大桥（自锚式悬索桥）采用的 E 形钢阻尼装置［17］，图1（c）为土耳其某高架桥梁（简支梁桥）伸缩缝处采用的C 形钢阻尼装置［18］。

对于采用钢阻尼装置实现双向震动控制则在中等跨径桥梁中更为常见，特别是连续梁桥，如图2（a）为柱形钢阻尼装置在吉林松原二桥引桥（连续梁桥）中提供双向阻尼力的案例［19］，对于其他类型的钢阻尼器提供双向阻尼力时，通常与支座结合在一起组成弹塑性钢阻尼支座，常见的钢阻尼支座见图2（b）和图2（c）。

图1 钢阻尼装置在单向震动控制中的应用Fig.1 Steel damping devices for the unidirectional seismic control

图2 钢阻尼装置在双向震动控制中的应用Fig.2 Steel damping devices for the bi-directional seismic control

上述钢阻尼装置的耗能原理均是利用金属材料屈服后的延性，只是构造形式不尽相同。尽管已有研究人员采用有限元软件和试验手段对某一类钢阻尼元件进行了详细的研究，但对同一目标参数需求下，不同构造形式的钢阻尼元件的比较研究并不多见。本文选取其中比较典型的柱形和E 形两类装置，首先对装置的工作原理、力学模型、技术实现等细节作了对比介绍，之后基于同一目标参数，设计完成了两类装置的足尺拟静力试验。结合试验结果，对两类钢阻尼装置的滞回行为、破坏形态、空间安装需求和材料用量等方面进行了详细的比较和分析。对桥梁工程师根据空间要求，地震动下桥梁震动控制模式选用和设计钢阻尼装置具有实际意义。

1 力学模型比较

柱形钢阻尼元件的力学模型为悬臂柱。力学图示见图3［20］。图中，F为悬臂端受到的水平力，Δ为钢阻尼元件水平行程，h为钢阻尼器高度，εmax为钢阻尼元件表面的最大应变，σy为屈服应力。

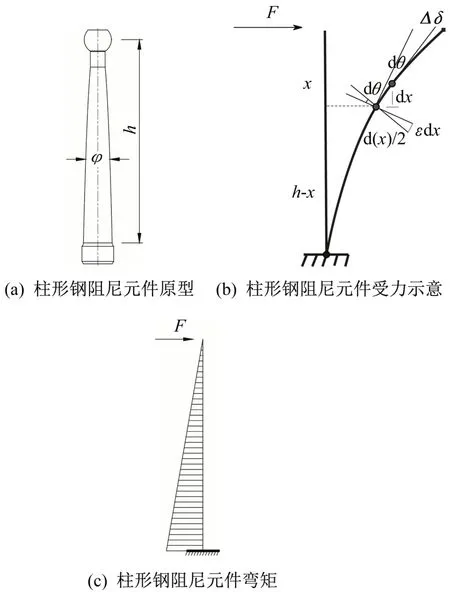
图3柱形钢阻尼装置力学模型Fig.3 Mechanical model of cylindrical device

由平截面假定得到柱形钢阻尼元件高度与行程之间的关系［4］：

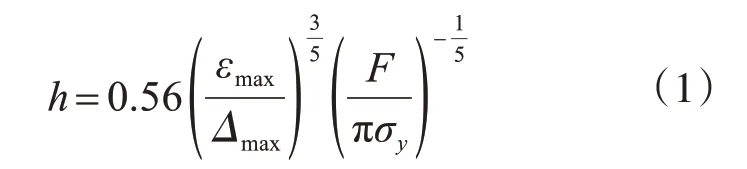
E 形钢阻尼元件可简化为两边铰接、中间简支的梁模型。如图4 所示，中间支座上作用力为F［20］，εmax为钢阻尼元件表面的最大应变，εy为钢材的屈服应变。

图4 E形钢阻尼装置力学模型Fig.4 Mechanical model of E-shaped device

E形钢阻尼元件的行程由式（2）得到［21］：

对于柱形阻尼元件，当元件发生变形时悬臂柱尽可能长的部分共同屈服而不是仅仅某一小段钢材提前进入屈服，即悬臂柱的母线是基于等应变原理进行设计的，在悬臂端受水平力作用下全柱各断面的表面应变处处相等，图5（a）为沿受力方向的应变分布情况示意。对于E 形元件，横梁段即为等弯矩受力段，当阻尼元件发生变形时，横梁段同时进入屈服，沿横梁长度方向断面的表面应变处处相等，应变分布情况示意见图5（b）。

图5 两类钢阻尼元件沿受力方向应变云图Fig.5 Strain cloud diagram of two kinds of dampers

2 技术实现比较

2.1 单向震动控制

2.1.1 纵桥向单向震动控制

为提高连续梁桥纵桥向抗震性能而设置柱形钢阻尼装置时，要求装置能够适应主梁在纵桥向由于温度效应产生的伸缩位移。对于一般跨径的连续梁桥，跨中附近活动墩处主梁温度位移在1～2 cm，此位移量可通过球头与推力槽之间预留间隙的方式实现，如图6所示。

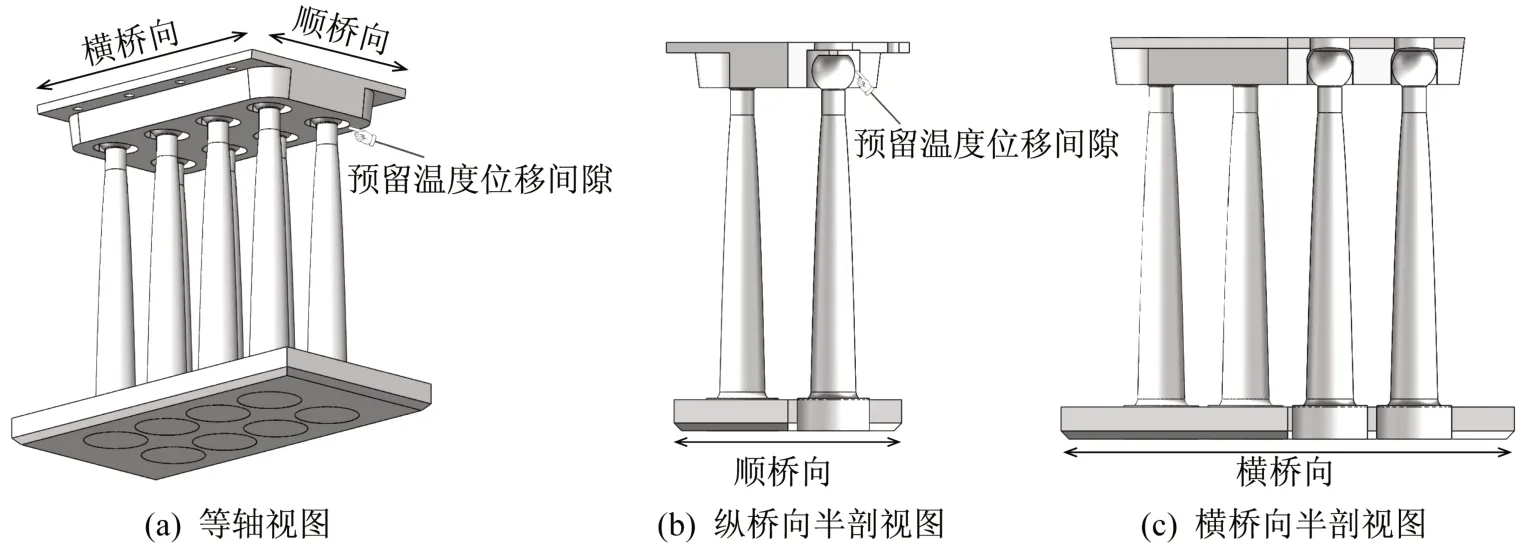
图6 柱形钢阻尼装置（纵桥向单向震动控制）Fig.6 Cylindrical steel damping device construction for longitudinal vibration

对于E 形，同样通过预留间隙的方式满足主梁在温度作用下自由伸缩而不受力的要求，见图7。

图7 E形钢阻尼装置（纵桥向单向震动控制）Fig.7 E-shaped steel damping device construction for longitudinal vibration

2.1.2 横桥向单向震动控制

以大跨度斜拉桥横向控制为例，大桥辅助墩、过渡墩等构件在地震作用下，为缓解横桥向受力的情况，通常设置钢阻尼装置，既限制墩-梁相对位移在可接受的范围内，又不明显增加墩柱受力。此时要求钢阻尼装置在桥梁结构正常使用状态下纵桥向的位移；在地震过程中，提供横向阻尼力，控制墩-梁相对位移。

如图8 所示，柱形钢阻尼装置耗能部件的球头可以在上述滑槽中沿纵桥向滑动，滑动距离视梁体在温度和徐变等因素下伸缩量而定，对于斜拉桥辅助墩、过渡墩而言，该伸缩距离一般为20～60 cm。地震作用下，球头与横桥向槽壁接触，变截面柱在该方向发生变形、提供阻尼力。

E 形钢阻尼装置提供横桥向阻尼力时，对于布设在活动墩的情况，同样须考虑主梁伸缩位移的要求。若此时沿中间肢长度方向开设槽孔，地震作用下，阻尼力方向与槽孔垂直，使得销轴处受力异常复杂。本文提出一种可滑移E形钢阻尼装置的构造，如图9 所示，中间肢通过滑块和滑轨装置与主梁连接，正常使用状态下，主梁可通过滑动装置沿纵桥向自由滑动；地震作用下，滑轨通过与滑块在横桥向的接触促使E形阻尼元件发生指定方向变形，在墩梁之间提供相应阻尼力。需要特别说明的是，它能很好满足纵桥向主梁大伸缩位移的要求。

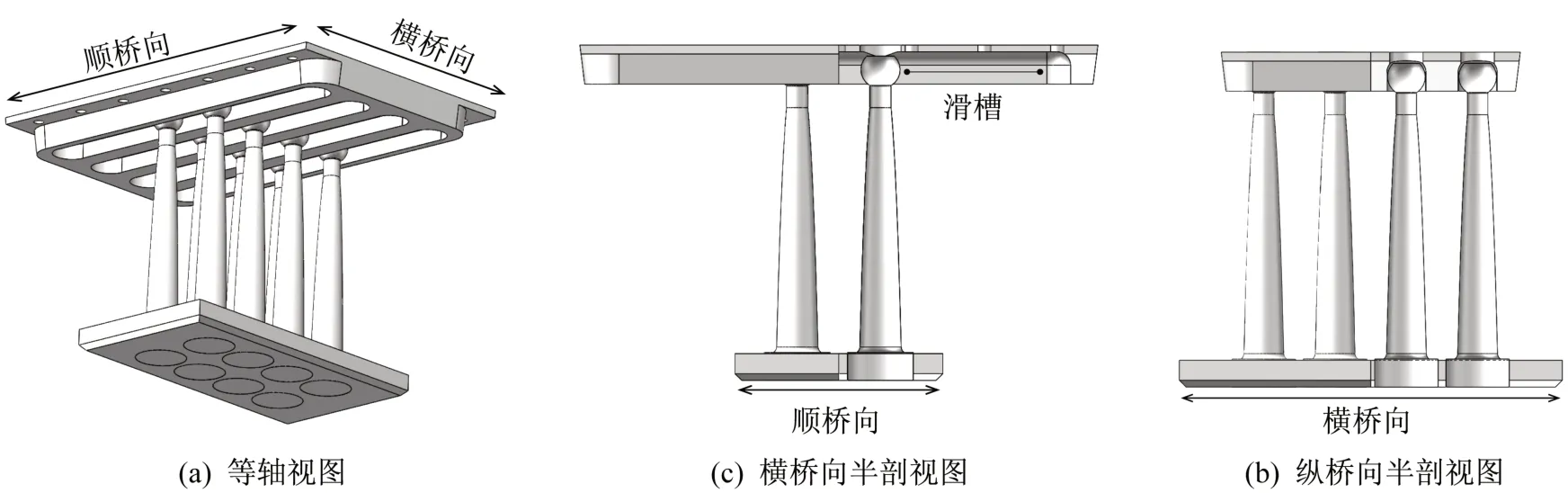
图8 柱形钢阻尼装置（横桥向单向震动控制）Fig.8 Cylindrical steel damping device construction for lateral vibration

图9 E形钢阻尼装置（横桥向单向震动控制）Fig.9 E-shaped steel damping device construction for lateral vibration

另外，E 形钢阻尼元件也可以与支座组合在一起成为弹塑性钢阻尼支座提供单向阻尼力。支座本体可以是盆式支座或者球形支座，该种支座通常由“上顶板”“中间衬板”“下底板”组成。为使主梁沿顺向自由伸缩，“上顶板”“中间衬板”之间设置滑动摩擦副；“中间衬板”“下底板”之间设置导向滑块和导向滑槽，并沿横桥向设置E形元件，见图10。地震作用下阻尼元件通过导向系统发生指定方向的变形，使得E 形元件的等弯矩横梁段发生塑性变形，产生良好的耗能效果。

图10 E形钢阻尼支座（横桥向单向震动控制）Fig.10 E-shaped steel damping bearing construction for lateral vibration

2.2 双向震动控制

连续梁桥活动墩、固定墩等构件在地震作用下，有时需要实现双向震动控制。对于柱形，针对连续梁桥活动墩的情况，球头与槽壁间预留间隙为1～2 cm，与钢阻尼装置的设计行程（一般情况下为20～40 cm）相比较小，见图11，此时钢阻尼装置仍具有较好的耗能效果。针对固定墩的情况，则间隙预留量为0。

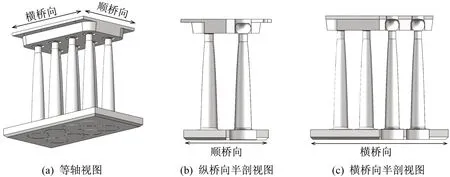
图11 双向控制时柱形钢阻尼装置构造形式Fig.11 Cylindrical steel damping device construction for bi-directional vibration

如图12 所示，E 形钢阻尼元件提供双向阻尼力时，阻尼元件沿两个方向分别设置，同时配合支座的“上顶板”“中间衬板”“下底板”组成的导向系统使用。针对活动墩情况，与柱形相类似，支座耳板预留温度滑槽，预留间隙一般为1～2 cm，适应主梁纵桥向位移。针对固定墩，间隙量同样设置为0。

图12 双向控制时E形钢阻尼装置构造形式Fig.12 E-shaped steel damping device construction for bi-directional vibration

3 滞回行为比较

基于模块化的设计思想，不同屈服力的钢阻尼装置可以由不同数量的标准组件组合得到，它们在力学上是简单的并联关系。本节结合设计实例，对柱形和E形的标准组件进行足尺模型试验，讨论分析两类装置的差异。标准组件的设计屈服力为250 kN，设计行程Δd为300 mm。参考《公路桥梁弹塑性钢减震支座》［22］，钢阻尼元件试验时按正弦波加载，幅值分别为0.25Δd（5 次循环）、0.5Δd（5 次循环）、Δd（10 次循环），加载平均速率为2 mm/s。

3.1 柱形钢阻尼元件拟静力试验

3.1.1 试件加工与制作

柱形阻尼元件由上海材料所的阻尼钢加工制作，钢材屈服强度为345 MPa。基于阻尼元件目标参数及柱形阻尼元件的设计表达式（1），得到柱形钢阻尼元件尺寸见图13。考虑元件需抵抗剪力和实际情况中与球头连接的构造要求，本案例在柱体上部设计了长度为96 mm 的等直段，端部设置有球头，保证阻尼元件受力方向指向球心。

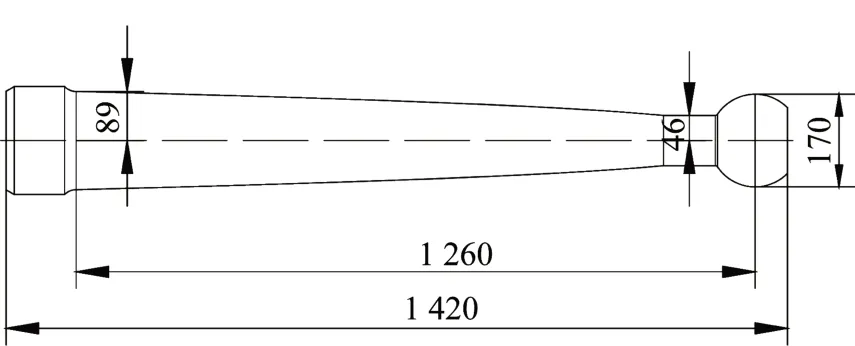
图13 柱形阻尼元件尺寸（单位：mm）Fig.13 Cylindrical damper dimensions（Unit：mm）

3.1.2 试验过程与现象

试验在同济大学土木工程防灾国家重点实验室进行，阻尼元件通过高强螺栓分别与顶板与地面连接。试验时，阻尼元件上方为加载端，下方为固定端，部分试验情况见图14。

图14 柱形阻尼元件试验情况Fig.14 Cylindrical damper test setup

试验结束过程中至试验结束后，阻尼元件未出现断裂及裂纹，且其他部位也无失效现象。

3.1.3 试验结果

测试项目有三项：作动器水平推力、阻尼元件关键位置位移、关键位置处应变，作动器伺服加载系统测量水平推力；采用拉线式位移计（量程500 mm 与200 mm）测量阻尼器元件水平位移。位移计自等直段与变截面段交界处向下间隔200 mm均匀布置，应变测点自等直段与变截面段交界处向下间隔150 mm 设置。相关测点分布情况见图15。

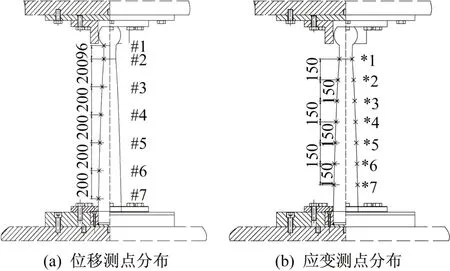
图15 柱形元件测点分布情况（单位：mm）Fig.15 Distribution of measuring positions（Unit：mm）

球头处（#1 号测点）的荷载位移曲线见图16，柱形表面中间部分（*3 号、*4 号、*5 号测点）的应变响应见图17。图17 中应变测量结果进一步论证了阻尼元件等应变的工作原理，即悬臂端受水平力作用下各断面的表面应变相等。实际情况中，由于柱形阻尼元件截面为圆形，实际贴片位置与理想测点不可避免存在一定偏差，使得图中各测点应变响应有所差异。后续试验过程当中，阻尼元件承受往复水平荷载，温度上升剧烈，使得应变测点很快失效。

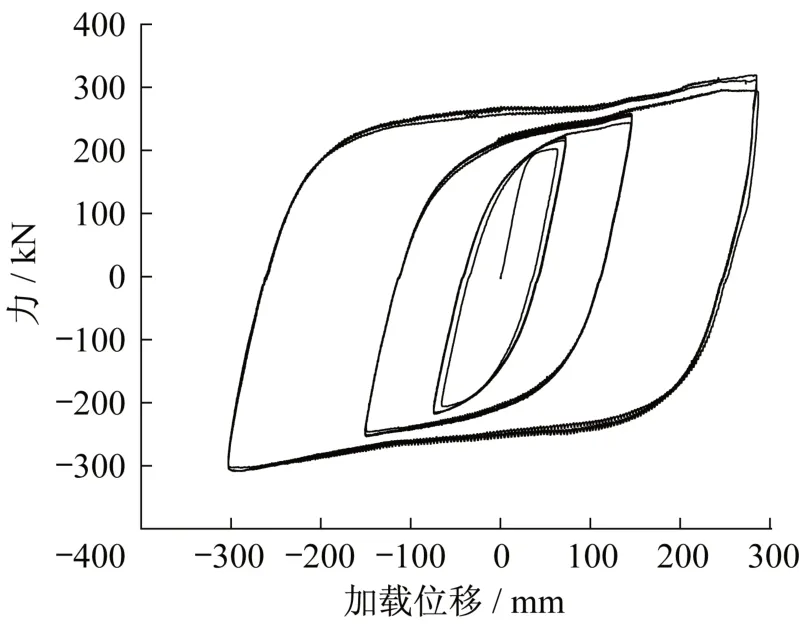
图16 球头处荷载-位移试验曲线Fig.16 Force-displacement test curve

图17 部分测点应变响应Fig.17 Strains at measuring positions

3.2 E形钢阻尼元件拟静力试验

3.2.1 试件加工与制作

E 形阻尼元件同样由上海材料所的阻尼钢加工制作，基于阻尼元件目标参数及柱形阻尼元件的设计表达式（2），得到E形钢阻尼元件尺寸见图18。需要说明的是，设计计算得到的E 形阻尼元件厚度为50 mm，出于市场供货及成本原因，实际采用70 mm的板材进行加工制作。

图18 E形阻尼元件尺寸Fig.18 E-shaped damper dimensions

3.2.2 试验过程与现象

对单片E 形阻尼元件进行试验时，通过反力架、滑块与导轨、地锚等系列装置配合，采用作动器对阻尼元件进行加载，部分试验情况见图19。

图19 E形阻尼元件试验情况Fig.19 E-shaped damper test setup

试验结束过程中至试验结束后，阻尼元件未出现断裂及裂纹，且其他部位也无失效现象。

3.2.3 试验结果

测试项目有三项：作动器水平推力、阻尼元件关键位置位移、关键位置处应变，相关测点分布情况见图20。

图20 E形元件测点分布情况（单位：mm）Fig.20 Distribution of measuring positions（Unit：mm）

中间销轴处（#1 号测点）的荷载位移曲线见图21，横梁段立面中间部分（*11号、*15号、*19号测点）及边肢部分（*1 号、*2 号测点）的应变响应见图22。图22 中横梁段应变测量结果与柱形情况类似，充分说明了阻尼元件发生变形时，等弯矩横梁段同时进入屈服，表现为沿横梁长度方向断面的表面应变相等。边肢部分的应变响应远小于横梁段，响应规律与图5 中应变云图一致，即边肢不参与耗能。

3.3 试验滞回行为比较

由于E 形阻尼元件的目标厚度为50 mm，阻尼元件的设计屈服力与厚度s呈线性关系［20］，在与柱形元件进行比较，E 形试验结果需要乘以一个5/7 的算子进行修正。二者力—位移试验曲线见图23。由图可知，基于相同的目标设计参数，可以看到，两类钢阻尼元件试验力学行为基本相同。

图21 中间销轴处荷载-位移试验曲线Fig.21 Force-displacement test curve

图23 两类钢阻尼元件试验结果对比Fig.23 Comparison of test results

在评述钢阻尼元件屈服力、屈服位移等参数时，将试验结果得到的力—位移曲线等效成双线性模型。等效原则如下：根据包围面积相等将实测的力—位移曲线等效，具体过程见图24。首先按初始卸载刚度作直线ME，同时过N点作ME的平行线线NF（M点、N点为卸载点），然后依据包围面积相等，确定点P和点Q位置。

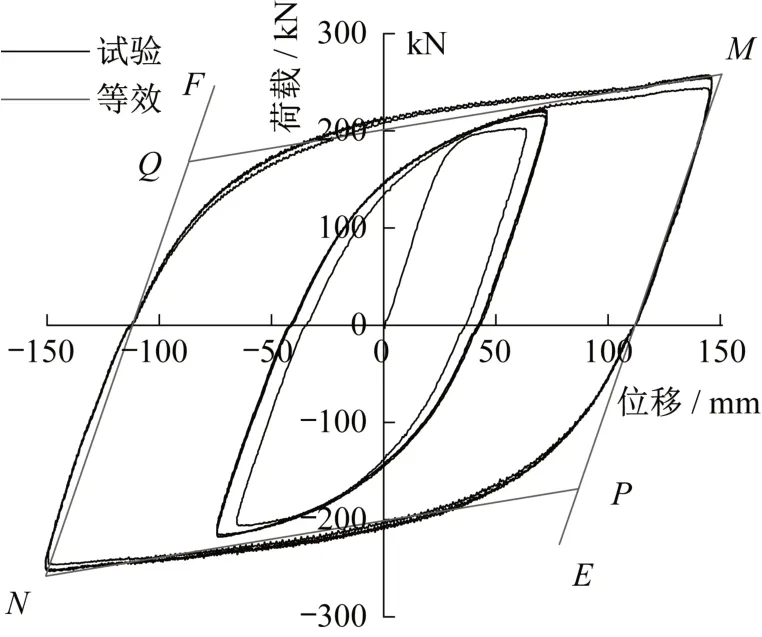
图24 双直线模型等效原则说明示意图Fig.24 Schematic diagram of equivalent principle

三种位移条件下其第三圈屈服力状态见图25，二者滞回行为基本相同，文中以柱形元件为例，按面积相等的原则将荷载—位移曲线等效成双直线模型，对屈服力、屈服位移、强度硬化系数（屈服后刚度/弹性刚度）等参数进行说明，具体数值见表1。

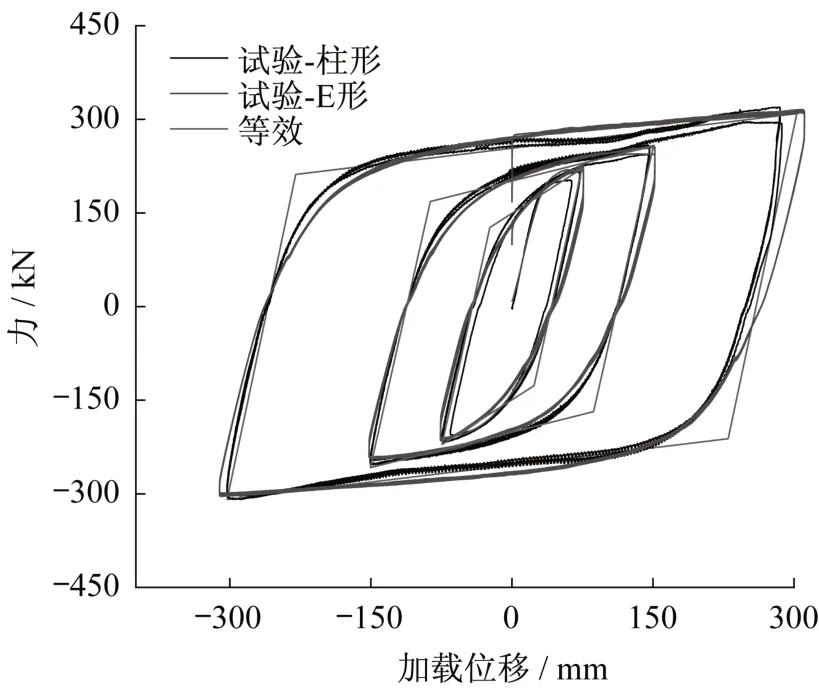
图25双直线模型等效结果Fig.25 Equivalent model of test results

表1 钢阻尼元件试验结果Table 1 Test results of steel damper

由表1 中数据可知，三种位移条件实测屈服力的平均值为226 kN，与设计值偏差为-9.5%；实测屈服位移的平均值为33 mm，与设计值偏差为10%；三种位移条件下强度硬化系数的平均值为7.4%。文中两种钢阻尼元件的最大延性系数，即最大加载位移（300 mm）与实测屈服位移（33 mm）的比值为9，需要特别说明的是，加载到300 mm时，阻尼元件尚未发生破坏，真实的最大延性系数会更高。

4 破坏形态比较

按第3 节中规定制度完成加载后，两种阻尼元件均为出现破坏现象，之后进行了探索性的破坏试验。对于柱形和E 形元件，以不同平均加载速度在设计位移下按正弦波形加载，为了更接近地震中墩-梁实际相对速度，试验中最大加载速度为100 mm/s，具体加载速度及循环周数见表2。

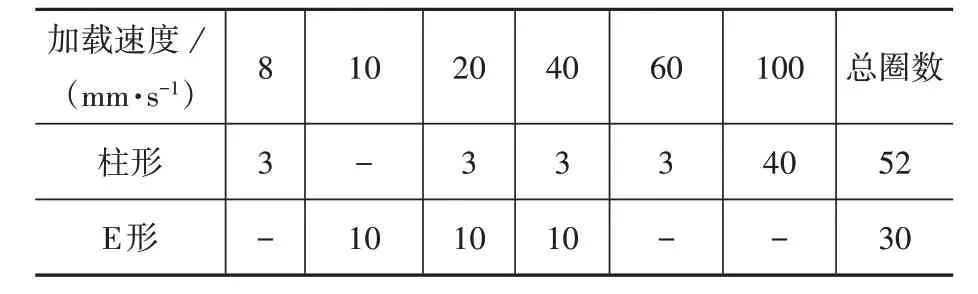
表2 破坏性试验加载情况Table 2 Destructive test loading

累加标准位移试验已经进行的10 周循环加载，柱形元件在62 周后发生断裂，E 形则为40 周。两类元件均在耗能段发生断裂失效，具体情况见图26。由于快速往复加载，钢材发生急剧的塑性变形，温度不断升高，红外线测温仪测到试验结束时柱形元件最高温度为320 ℃，高温导致柱形阻尼元件断口呈黑褐色，见图26（a），此时采集应变与位移的导线已经烧灼。关于E 形，由于加载速度略低于柱形情况，试验结束时测到的最高温度为205 ℃，在等弯矩横梁段发生破坏，部分导线由于高温发生燃烧现象，见图26（b）。

破坏性试验全过程试验曲线见图27，阻尼元件直至发生破坏前，滞回曲线仍然饱满。参考各国文献对其加载周数的要求［23-24］，文中两种钢阻尼元件循环周数满足一般地震荷载下的要求，且均表现出较好的耗能特性。

图26 两类钢阻尼元件破坏形态Fig.26 Failure mode of dampers

图27 破坏性试验全过程试验曲线Fig.27 Test results of destructive test

5 材料用量及空间需求比较

5.1 材料用量比较

基于相同设计参数得到的两类钢阻尼元件尺寸分别见图13 和图18，图中，柱形元件高度为1 450 mm，E 形元件两边肢销孔之间距离为1 740 mm，前者对竖向安装空间提出了较高的要求，后者则对平面空间需要更高。关于材料用量，柱形元件为163 kg，E 形元件按0.71 算子修正后用量为268 kg，柱形节省近40%。主要因为E 形元件三个肢不参与变形耗能，这一点可从图5 中的应变云图及图22 所应变测点响应中看出。如提供双向阻尼力时，材料用量会进一步节省，因为柱形元件截面为圆形，一个阻尼元件可同时提供两个方向的阻尼力，不再需要沿两个方向分别设置［4，20］。

5.2 空间需求比较

大跨度斜拉桥抗震设计中，顺向一般采用黏滞型阻尼器，横向则采用钢阻尼装置。对于辅助墩、过渡墩等构件，墩柱系梁和主梁之间一般会有足够的安装空间，两类钢阻尼装置同等适用。

中小跨径梁式桥抗震设计中，对于喇叭形桥墩或者有系梁情况，见图2（a），墩-梁之间竖向空间充足，若要求提供双向力，实现双向震动控制模式时，优先采用立式柱形钢阻尼装置，见图28，优点有两个：其一可节省阻尼元件的材料用量；其二相比于E 形元件需要配合支座导向系统而言，传力路径更加清晰简单。

图28 立式柱形钢阻尼装置构造形式Fig.28 Constructions of stand-type cylindrical device

多数情况下，墩-梁之间竖向距离一般在50 cm 以内，更适合E 形元件的使用。为发挥柱形元件节省材料的优势，本文提出一种卧式柱形钢阻尼装置，见图29。柱形元件水平设置，底部通过锚板与主梁连接，为使棒体始终受水平方向的作用力，球头中心处设置有销轴，以保证力的作用点始终指向球心。同时销轴的设置使得球头通过导向架沿纵桥向在导向滑槽内自由滑动。地震时，导向滑槽带动球头受力。该装置空间需求与E形情况相当，在钢阻尼方案比选时，成本优势较为明显。

图29 卧式柱形钢阻尼装置构造形式Fig.29 Constructions of horizontal-type cylindrical device

6 结论与建议

本文首先对比介绍了柱形和E形钢阻尼元件的力学模型及技术实现途径，基于具体的设计实例，完成了两类钢阻尼元件足尺模型试验，结合试验结果在滞回行为、破坏形态、材料用量、空间需求等方面得到以下结论和建议：

（1）构造形式。本文清晰地梳理了桥梁震动控制中，单向震动控制（包括纵桥向和横桥向）模式、双向震动控制模式下，各类柱形和E形阻尼装置的构造形式，方便设计和研究人员选取采用。

（2）滞回行为。足尺试件的拟静力试验结果表明，相同的目标参数下，柱形和E形钢阻尼元件的滞回行为基本相同。

（3）破坏形态。两类钢阻尼装置均在设定的耗能段发生断裂失效。需要特别说明的是耗能段由于发生快速往复变形，钢材温度急剧升高，对文中例柱形情况，在设计位移循环加载62 周后，温度达305 ℃，这是由钢材急剧往复进入塑性变形引起的，该段区域最后因此发生严重损伤而断裂失效。

（4）材料用量。实现桥梁震动的单向控制时，柱形钢阻尼装置与E 形相比更为节省。这是因为E 形元件三个肢并不参与变形耗能，对本文例节省近40%。双向震动控制时，立式柱形钢阻尼装置材料用量相比于单向控制时会进一步减少，这是因为一个立式柱形元件可以同时提供双向阻尼力。

（5）空间需求。传统的立式柱形钢阻尼装置对竖向安装空间要求较高，实践应用中受到一定限制。本文提出一种卧式柱形装置，空间需求与E 形情况相当，为发挥柱形材料的成本优势提供可行的技术途径。