型钢混凝土剪力墙基于性能的有害层间位移角限值研究

李莹辉 蒋欢军

（1.同济大学土木工程防灾国家重点实验室，上海200092；2.同济大学土木工程学院，上海200092；3.华东建筑设计研究院有限公司，上海200011）

0 引 言

剪力墙结构在地震作用下的侧向变形形式为弯曲型，损伤往往发生在墙肢底部［1］。墙肢底部的弯曲变形引起的转角将引起墙肢上部较大的刚体转动，导致最大层间位移角往往发生在墙肢上部，而上部墙肢的刚体转动并不会直接引起墙肢的损伤。因此，许多学者［2-5］提出采用扣除墙肢刚体转动后的有害层间位移角作为剪力墙墙肢的变形指标，其定义为结构某层中某单片墙肢在该层的侧向变形减去下层墙肢转动引起该层墙肢的刚体转动，然后除以该层层高。

剪力墙结构基于位移的抗震设计需要对剪力墙的变形指标给出不同性能等级的变形限值。美国规范ASCE41-13［6］采用塑性铰模型并假定塑性铰长度为墙肢长度的一半给出了弯曲破坏的钢筋混凝土剪力墙不同性能等级的塑性转角限值，劳晓春等［7］采用有限元模型并假定塑性区高度为墙肢长度的一半，给出了弯曲破坏的钢筋混凝土剪力墙在极限状态时的塑性转角限值。然而，根据许多学者［8-10］的钢筋混凝土剪力墙的拟静力试验研究，墙肢底部塑性区的发展高度大于塑性铰模型中假定的高度（0.5倍墙肢长度），而按照规范正常设计的剪力墙，结构层高与墙肢长度的比值在0.5 与2 之间，因此，剪力墙结构的层高可能小于剪力墙的塑性区发展高度，也可能大于剪力墙的塑性区发展高度。若采用塑性铰模型并假定塑性区等效集中在假定的塑性铰高度范围，将计算得到的塑性铰转角限值作为剪力墙有害层间位移角限值将可能高估层高较小剪力墙结构的变形能力，如图1（a）所示。而采用有限元模型且仅计算假定塑性区（墙肢长度的一半）的转角限值作为剪力墙有害层间位移角限值将可能低估层高较大剪力墙结构的变形能力，如图1（b）所示。

对于试验数据不足的结构构件，常采用有限元分析的方法得到结构构件不同性能等级的变形限值［11-12］。相对于一维和二维有限元模型，三维实体单元对于构件局部损伤的模拟更为精细［13］。一维杆单元无法准确模拟剪力墙的剪切变形，二维平面单元无法准确模拟构件中型钢或钢筋与混凝土之间的相互作用，而三维实体单元不仅可以模拟构件的弯曲变形，还可以模拟构件的剪切变形及钢筋或型钢与混凝土之间的相互作用。

图1 墙肢转角限值的两种计算方法Fig.1 Two methods of calculating wall pier rotation limit

在高层建筑结构中，型钢混凝土剪力墙因其较高的承载力及良好的延性和耗能能力得到了广泛的应用，但关于其变形指标限值的研究较少。本文以弯曲破坏的型钢混凝土剪力墙为分析对象，提出在剪力墙有害层间位移角限值计算中应考虑层高的影响。采用经过验证的三维有限元分析模型对型钢混凝土剪力墙进行参数分析，得到不同性能等级的有害层间位移角限值，为高层钢-混凝土组合结构基于性能的抗震设计提供参考。

1 型钢混凝土剪力墙性能等级划分

对于弯曲破坏的型钢混凝土剪力墙，根据已有的拟静力试验研究［14-16］，其损伤顺序及破坏模式与弯曲破坏的型钢混凝土柱类似。试验过程中出现的损伤特征点包括混凝土开裂、纵筋受拉屈服、混凝土保护层压碎、混凝土保护层剥落、纵筋压屈、型钢压屈、纵筋拉断以及型钢拉断等。这些材料的损伤与材料在试件拟静力试验过程中经历的最大应变息息相关［13，17］。此外，我国建筑抗震设计规范［18］中对于中等破坏及不严重破坏性能等级提出了控制结构构件承载力降低程度的要求。结合作者之前关于型钢混凝土柱变形指标限值的研究［12］，本文提出型钢混凝土剪力墙基于应变与承载力的性能等级划分方法，如表1 所示。表中εcu为混凝土极限压应变，按照 Priestley 等［19］建议的公式进行计算，Fmax为型钢混凝土剪力墙抗侧承载力峰值。由表1 性能等级划分方法得到的性能点与构件荷载-位移骨架曲线特征点的关系如图2所示。

表1 型钢混凝土剪力墙性能等级划分方法Tab.1 Method of dividing performance levels for steel reinforced concrete walls

图2 剪力墙试件性能点与特征点的关系Fig.2 Relationship between performance points and characteristic points of shear wall specimen

2 有限元模型验证及设计

采用通用有限元软件ABAQUS 对型钢混凝土剪力墙进行不同性能等级下的变形限值分析。混凝土采用三维实体单元C3D8R，剪力墙端部型钢采用二维壳单元S4R，纵筋及箍筋采用一维桁架单元T3D2。不考虑型钢与混凝土以及钢筋与混凝土之间的粘结-滑移，通过固结模型底面，在模型顶部建立参考点，且将剪力墙顶面与参考点耦合，而将荷载施加在参考点上。

选取Ji等［14］完成的型钢混凝土剪力墙拟静力试验试件SRCW1 作为分析对象，其剪跨比为2.43，试验轴压比为0.32，试件发生弯曲破坏，截面尺寸与配筋信息如图3 所示（两边对称）。根据箍筋与型钢对混凝土约束的大小，将混凝土截面划分为低约束区，中约束区及高约束区，如图4（a）所示（两边对称）。剪力墙非端部约束区的混凝受箍筋约束作用较小，采用无约束混凝土本构关系，中约束区的箍筋约束混凝土采用Mander 本构关系［20］，高约束区的工字钢约束混凝土采用Chen 等［21］通过试验校验得到的约束提高系数计算，不同约束区的混凝土应力-应变骨架曲线如图4（b）所示。钢材均采用强化的二折线本构模型，强化段刚度为初始刚度的0.01 倍。试件SRCW1的有限元模型如图5所示。

图3.试件SRCW1截面尺寸与配筋（单位：mm）Fig.3 Section dimension and reinforcement arrangement of specimen SRCW1（Unit：mm）

图4 约束混凝土本构关系Fig.4 Constitutive model of confined concrete

图5 试件SRCW1的三维有限元模型Fig.5 Three dimensional finite element model of specimen SRCW1

有限元分析的结果与试验结果对比如图6 所示。可以看出，三维有限元模型能够较好地模拟试件损伤的发展以及试件整体侧向刚度、承载力的变化。因此，采用三维有限元模型进行型钢混凝土剪力墙不同性能等级的变形限值研究是合理可靠的。

图6 有限元分析与试验结果对比Fig.6 Comparison of finite element analysis and test results

型钢混凝土剪力墙端部内置型钢的形式可以有多种选择［14］，如工字型、槽钢、矩形钢管和圆钢管等。而工程中应用较多的是内置工字钢［22］，因此本文设计的型钢混凝土剪力墙内置型钢仅采用工字钢一种形式。已有试验结果［14-16］表明，型钢混凝土剪力墙的侧向变形能力随轴压比的增大而减小。组合结构设计规范［22］通过限制轴压比来保证型钢混凝土剪力墙具有足够的变形能力，规范关于不同抗震等级的型钢混凝土剪力墙轴压比限值的最大值为0.6。本文设计的型钢混凝土剪力墙的设计轴压比分别为 0.1、0.25、0.4、0.55 四种。关于型钢混凝土剪力墙边缘约束构件的最小和最大含钢率，至今没有统一的认识。根据白晓红等［23］的研究，常用的型钢混凝土剪力墙边缘构件含钢率范围为4%～8%，且变形能力随含钢率的增加而增加。本文设计的型钢混凝土剪力墙边缘构件含钢率分别为3%、5%、7%三种，截面尺寸如图7（两边对称）和表2 所示，钢材选用Q235 钢，剪力墙截面宽度B为300 mm，截面长度L为2 400 mm。组合结构设计规范［22］对型钢混凝土剪力墙边缘约束构件的最小体积配箍率进行了规定，最小配箍率和轴压比限值与抗震等级相关，常用的体积配箍率为1%左右。本文设计的型钢混凝土剪力墙边缘构件体积配箍率为0.80%、1.15%和1.56%三种，纵筋和箍筋均采用HRB400 钢筋，箍筋布置分别为10@10012@100、14@100。

图7 型钢混凝土剪力墙算例截面尺寸示意图Fig.7 Schematic diagram of section dimension of steel reinforced concrete shear wall

表2 型钢混凝土剪力墙内置型钢截面尺寸Tab 2 Section dimension of steel reinforced concrete shear walls

型钢混凝土剪力墙在水平荷载作用下主要有三种破坏模式：剪切破坏、弯剪破坏和弯曲破坏。当剪跨比大于2 且满足强剪弱弯的设计时，试件一般先发生弯曲破坏。本文主要针对弯曲破坏的型钢混凝土剪力墙进行研究，所设计的型钢混凝土剪力墙剪跨比有2、3 和4 三种。其余参数均不变，混凝土采用50，端部约束区长度为500 mm，端部纵筋为620，横向和竖向分布筋均为12@150，材料强度均采用标准值。因此，本文共设计了 108 片（4×3×3×3=108）型钢混凝土剪力墙，对ABAQUS 软件进行二次开发，对所设计的型钢混凝土剪力墙进行参数化建模、分析及后处理，提高了工作效率。

3 有害层间位移角限值

按照规范正常设计的剪力墙结构层高与墙肢长度的比值在0.5 与2 之间，剪力墙真实塑性区高度有可能大于层高，而且弯曲破坏的型钢混凝土剪力墙在塑性区仍会发生较大的塑性剪切变形［15，24］。由墙肢底层弯曲变形引起的墙肢顶部侧向位移角θT要大于墙肢底层侧向位移角θS，而由墙肢底层剪切变形引起的墙肢顶部侧向位移角θT要小于墙肢底层侧向位移角θS，变形分析示意如图8所示。

图8 底层位移角与试件顶点位移角对比示意Fig.8 Comparison of bottom story drift and top drift for shear wall specimen

因此，型钢混凝土剪力墙算例侧向加载点处的位移角限值并不等于底层层间位移角限值。本研究针对每个型钢混凝土剪力墙算例，假定层高与墙肢的长度比值分别为0.5、1.0、1.5 和2，求取4个计算层高处的侧向割线位移角（包括弯曲变形与剪切变形）作为型钢混凝土剪力墙有害层间位移角限值。

3.1 “基本完好”

按照前述方法得到型钢混凝土剪力墙在“基本完好”性能等级下的有害层间位移角限值频率分布直方图如图9（a）所示。采用对数正态分布函数对其进行拟合，得到对数正态分布的众值（出现频率最高的点）为0.001 1 rad。将拟合得到的对数正态分布函数积分得到累积对数正态分布即易损性曲线与有限元计算结果对比如图9（b）所示。函数与有限元数值较为吻合，中位值与84%保证率（均值减去一倍方差）的统计特征值分别为0.001 3 rad和0.000 9 rad。

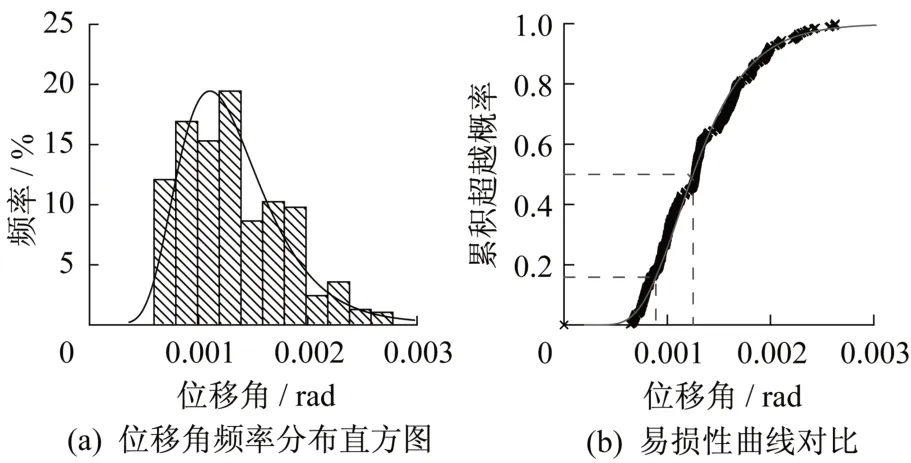
图9 “基本完好”位移角限值统计分析Fig.9 Drift limit statistical analysis for performance level of“basically intact”

采用Kruskal-Wallis 非参数方差分析检验各设计参数对“基本完好”位移角限值的影响。含钢率ρs、配箍率ρv和剪跨比λ等参数对“基本完好”位移角限值的P值大于0.05，认为这些参数对“基本完好”位移角的影响较小，不在位移角限值拟合公式中考虑。而“基本完好”位移角限值随轴压比μ与层高墙长比β的变化如图10 所示，位移角限值随轴压比增加减少，随层高墙长比增加而增加。采用幂指数函数进行数据拟合，得到“基本完好”层间有害位移角限值计算公式如下所示：

式（1）的决定系数（拟合优度）R2为0.92，拟合公式值与有限元值的对比如图11 所示。拟合公式值与有限元计算值的比值平均值为1.01，标准差为0.10，说明拟合公式计算结果较为准确。

图10 “基本完好”位移角限值随设计参数变化Fig.10 Variation of drift limit under performance of“basically intact”with design parameters

3.2 “轻微损伤”

型钢混凝土剪力墙在“轻微损伤”性能等级下的有害层间位移角限值频率分布直方图及易损性曲线如图12 所示。其分布众值、中位值以及84%保证率的统计特征值分别为0.004 7、0.005 1 以及0.003 9。

图11 “基本完好”位移角限值公式值与有限元值对比Fig.11 Comparison of formulation and simulation results for drift limits under performance level of“basically intact”

图12 “轻微损伤”位移角限值统计分析Fig.12 Drift limit statistical analysis for performance level of“slight damage”

采用Kruskal-Wallis 非参数方差分析检验各设计参数对“轻微损伤”位移角限值的影响。含钢率ρs、配箍率ρv和剪跨比λ等参数对“轻微损伤”位移角限值的P值大于0.05，认为这些参数对“轻微损伤”位移角的影响较小，不在位移角限值拟合公式中考虑。而“轻微损伤”位移角随轴压比μ与层高墙长比β的变化如图13 所示，位移角限值随轴压比增加减少，随层高墙长比增加而增加。采用幂指数函数进行数据拟合，得到“轻微损伤”层间有害位移角限值计算公式如下所示：

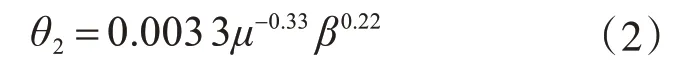
图13 “轻微损伤”位移角限值随设计参数变化Fig.13 Variation of drift limit under performance of“slight damage”with design parameters

式（2）的决定系数R2为0.88，拟合公式值与有限元值的对比如图14 所示。拟合公式与有限元计算值的比值平均值为1.01，标准差为0.09，说明拟合公式计算结果较为准确。

图14 “轻微损伤”位移角限值公式值与有限元值对比Fig.14 Comparison of formulation and simulation results for drift limits under performance level of“slight damage”

3.3 “中等损伤”

型钢混凝土剪力墙在“中等损伤”性能等级下的有害层间位移角限值频率分布直方图及易损性曲线如图15 所示。其分布众值、中位值以及84%保证率的统计特征值分别为0.008 7、0.009 7 以及0.007 1。

图15 “中等损伤”位移角限值统计分析Fig.15 Drift limit statistical analysis for performance level of“moderate damage”

采用Kruskal-Wallis 非参数方差分析检验各设计参数对“中等损伤”位移角限值的影响。层高墙长比β和配箍率ρv等参数对“中等损伤”位移角限值的P值大于0.05，认为这些参数对“中等损伤”位移角的影响较小，不在位移角限值拟合公式中考虑。而“中等损伤”位移角随轴压比μ、含钢率ρs与剪跨比λ的变化如图16 所示，位移角限值随轴压比增加而减少，随含钢率增加而增加，随剪跨比增加而增加。采用幂指数函数进行数据拟合，得到“中等损伤”层间有害位移角限值计算公式如下所示：

式（3）的决定系数R2为0.89，拟合公式值与有限元值的对比如图17 所示。拟合公式与有限元计算值的比值平均值为1.01，标准差为0.11，说明拟合公式计算结果较为准确。

图16 “中等损伤”位移角限值随设计参数变化Fig.16 Variation of drift limit under performance of“Moderate damage”with design parameters

图17 “中等损伤”位移角限值公式值与有限元值对比Fig.17 Comparison of formulation and simulation results for drift limits under performance level of“moderate damage”

3.4 “严重损伤”

型钢混凝土剪力墙在“严重损伤”性能等级下的有害层间位移角限值频率分布直方图及易损性曲线如图18 所示。其分布众值、中位值以及84%保证率的统计特征值分别为0.014 1、0.015 7 以及0.011 3。

图18 “严重损伤”位移角限值统计分析Fig.18 Drift limit statistical analysis for performance level of“severe damage”

采用Kruskal-Wallis 非参数方差分析检验各设计参数对“严重损伤”位移角限值的影响。层高墙长比β和含钢率ρs等参数对“严重损伤”位移角限值的P值大于0.05，认为这些参数对“严重损伤”位移角的影响较小，不在位移角限值拟合公式中考虑。而“严重损伤”位移角随轴压比μ、配箍率ρv与剪跨比λ的变化如图19 所示，位移角限值随轴压比增加减少，随配箍率增加而增加，随剪跨比增加而增加。采用幂指数函数进行数据拟合，得到“严重损伤”层间有害位移角限值计算公式如下所示：

式（4）的决定系数R2为0.85，拟合公式值与有限元值的对比如图20 所示。拟合公式与有限元计算值的比值平均值为1.02，标准差为0.14，说明拟合公式计算结果较为准确。

图19 “严重损伤”位移角限值随设计参数变化Fig.19 Variation of drift limit under performance of“severe damage”with design parameters

4 结 论

图20 “严重损伤”位移角限值公式值与有限元值对比Fig.20 Comparison of formulation and simulation results for drift limits under performance level of“severe damage”

（1）根据已有弯曲破坏的型钢混凝土剪力墙拟静力试验中观察到的试件损伤发展过程及破坏特征，结合材料应变及抗侧力下降程度，提出弯曲破坏型钢混凝土剪力墙性能等级的划分方法。

（2）考虑层高的影响，由三维有限元分析得到型钢混凝土剪力墙在不同性能等级的有害层间位移角限值。采用对数正态分布函数拟合，得到不同性能等级位移角限值的中位值、众值以及具有84%保证率的统计特征值。为型钢混凝土剪力墙结构简化的抗震性能设计和分析提供参考。

（3）本文提出的层高墙长比参数对“基本完好”“轻微损伤”性能等级的有害层间位移角限值影响较大，位移角限值随层高墙长比的增加而增加。而层高墙长比对“中等损伤”“严重损伤”性能等级位移角限值的影响可以忽略。

（4）各性能等级有害层间位移角限值均随轴压比的增加而减少。此外，“中等损伤”位移角限值随含钢率、剪跨比的增加而增加，“严重损伤”位移角限值随配箍率、剪跨比的增加而增加。