既有结构基于评估使用年限的目标可靠度研究

蒋利学 王卓琳

（上海市建筑科学研究院有限公司上海市工程结构安全重点实验室，上海200032）

0 引 言

我国现行规范将结构耐久性限定在正常使用极限状态范畴［1-2］，但很多情况下仍需要考虑耐久性抗力退化对结构安全性的影响［3-4］。在建筑结构设计标准的可靠度不断提高的情况下，既有结构可靠性评定时应该采用什么样的目标可靠指标？特别是当评估使用年限缩短时，目标可靠指标应如何作调整？当考虑耐久性抗力退化时，应该如何确定结构构件的使用安全寿命准则？这些问题是既有结构可靠性评定、寿命预测和维护决策中面临的基本问题。

我国现行结构设计统一标准［1-2］均未对既有结构可靠性评定提出专用的目标可靠指标，而在《建筑结构设计统一标准》（GBJ 68—84）［5］中曾规定：当有充分依据时，各类材料的结构设计规范中采用的目标可靠指标可对该统一标准规定值作不超过±0.25 的调整。这个规定被我国既有结构可靠性鉴定标准［6-7］作为确定b 级构件（可不采取措施）目标可靠度的依据，并被认为是我国统一标准规定的质量下限水准。

牛荻涛［8］在认为我国统一标准规定的设计目标可靠指标合理的基础上，根据既有结构在后续使用期内的年失效概率与结构在设计使用年限内的年失效概率相等的原则，给出了确定既有结构目标可靠指标的方法。但其提出的目标可靠指标随评估使用年限缩短而增大，即评估使用年限越短，可靠度水准要求越高，这与人们的直觉判断完全相反。

林拥军等［9］认为，考虑抗力退化的目标可靠指标实际上是评估使用年限内，起始时刻的最低可靠指标。他们根据不考虑抗力退化的目标可靠指标和抗力衰减函数计算设计使用年限结束时的目标可靠指标，再根据可靠性评定的评估使用年限结束时的目标可靠指标与原设计使用年限结束时的目标可靠指标相等的原则，反算评估使用年限起始时刻的目标可靠指标。显然，用这种方法确定可靠性评定所需的目标可靠指标时，需要事先确定抗力衰减函数，故在工程应用上有很大障碍。另一方面，该方法在确定目标可靠指标时实质上仅考虑了抗力退化的不利影响，而没有考虑评估使用年限缩短带来的有利影响。

总之，如何确定既有结构可靠性评定的目标可靠度，以及考虑抗力退化时的使用安全寿命准则，现有标准的规定或可供参考的文献资料很少，还有不少问题值得探讨。本文在分析比较国内外标准对结构目标可靠度和允许失效概率规定的基础上，研究了既有结构基于评估使用年限的目标可靠度设置准则，探讨了危险构件的可靠度定义和结构构件的使用安全寿命准则，以及对既有结构进行周期性检测评定的作用和意义。

1 国内外标准对结构目标可靠度和允许失效概率规定的比较

我国国家标准《工程结构可靠性设计统一标准》（GB 50153—2008）［1］和《建筑结构可靠度设计统一标准》（GB 50068—2018）［2］规定的建筑结构构件的目标可靠指标及其对应的允许失效概率见表1。这些数值均指设计使用年限内的允许累积失效概率及其对应的目标可靠指标。那么当既有结构可靠性评定采用小于原设计使用年限的评估使用年限时，目标可靠指标及其对应的允许累积失效概率是否可以作出调整？对这个问题两本统一标准均未作明确规定。应该指出，我国标准中没有从可接受风险角度确定的允许失效概率的概念，只有对应于目标可靠指标的失效概率运算值的概念。但对应于目标可靠指标的失效概率运算值也是一个允许值（上限值）的概念，故本文为了区别于结构实际失效概率，采用允许失效概率的概念。

表1 我国统一标准规定的结构构件目标可靠指标Table 1 Target reliable indexes for structural components in China's unified standards

国际结构安全性联合会（JCSS）出版的概率模式规范［10］规定的结构构件允许失效概率及其对应的目标可靠指标见表2。表中的允许年失效概率及其对应的目标可靠指标是JCSS 在对有典型代表性的简单结构进行投资-效益分析的基础上确定的，并且与校准分析和统计观察结果相一致。该规范［10］指出：失效后果根据总费用（失效的直接损失与建造费用之和）与建造费用之比分为小、中、大三类：其中“小”一般指失效对危及生命的风险和经济损失小甚至可忽略的结构，如仓库、农业建筑等；“中”一般指失效对危及生命的风险和经济损失中等的结构，如办公楼、住宅、工业建筑等；“大”一般指失效对危及生命的风险大和经济损失巨大的结构，如医院、剧院等大型公共建筑、高层建筑等。JCSS 概率模式规范还指出：尚应根据破坏模式对目标可靠指标进行调整，脆性破坏结构构件的目标可靠指标的取值应高于延性破坏的结构构件。从上述说明可以看出，该模式规范对失效后果的分类与我国统一标准［1-2］的结构重要性分类基本一致。

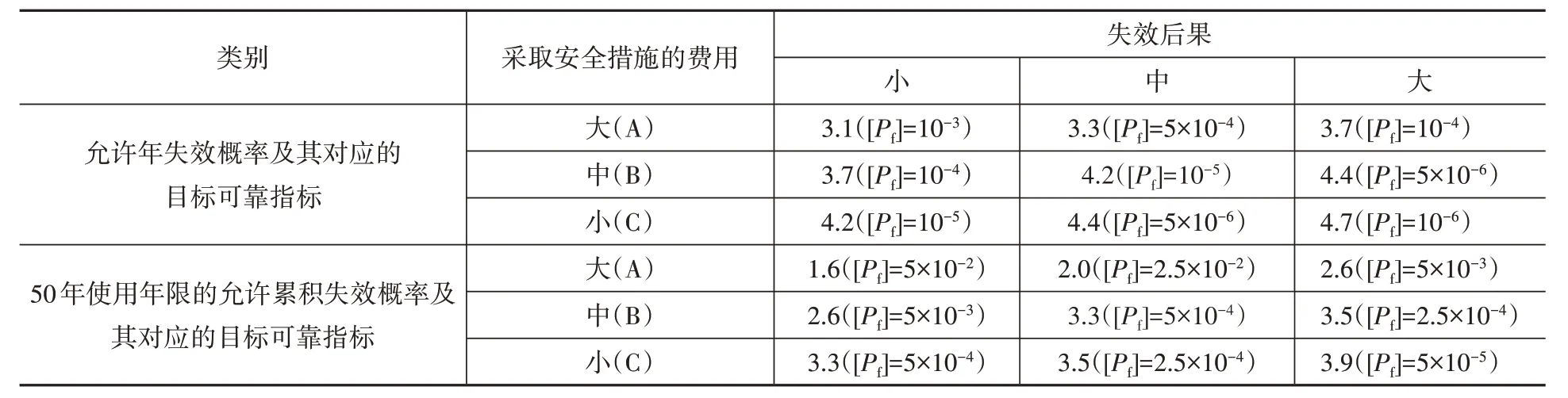
表2 JCSS模式规范规定的结构构件允许失效概率及目标可靠指标［10］Table 2 Allowable failure probability and target reliable index for structural components in JCSS mode code

JCSS 概率模式规范将“采取安全措施的费用”分为A、B、C或大、中、小三类，其中B类对应于一般结构，采用正常设计使用年限。可根据下列不同情况对可靠性等级进行调整［10］：

（1）不确定性程度。当不确定性很大（如发生偶然事件或罕遇地震）时，应选择较低的可靠性等级，因为在应对这种高度不确定性事件时，为获得过高的可靠性所付出的额外代价令人无法接受。

（2）质量保证和定期检查。对新结构加强质量保证措施或对既有结构加强定期检查会增加费用，这时可选用较低的可靠性等级。从另一方面讲，因为加强质量保证措施和定期检查可带来不确定性的降低，在相同条件下可获得更高的可靠性等级，从经济方面讲这是一种具有吸引力的处理方式。

（3）既有结构。相对于设计的拟建结构而言，既有结构要获得更高的可靠性所付出的代价更大。因此，既有结构可选择较低一些的可靠性等级。

（4）使用年限和拆除。对设计使用年限很短或拟快速拆除的结构构件（如使用年限少于10年），可靠性等级可低一个或半个等级。

一般房屋结构的设计使用年限为50 年，将JCSS 概率模式规范规定的允许年失效概率换算为50 年使用年限内的允许累积失效概率及其对应的目标可靠指标，结果也列于表2。可见，对一般结构而言，将允许年失效概率换算为50 年设计使用年限内的允许累积失效概率及其对应的目标可靠指标后，与我国统一标准［1-2］规定值基本相当。特别是最普通的结构构件，即失效后果和采取安全措施的代价等级均为“中”的结构构件，其50年设计使用年限内的目标可靠指标为3.3（允许累积失效概率［Pf］=5×10-4），而我国统一标准［1-2］中延性破坏的二级构件的目标可靠指标为3.2（允许累积失效概率［Pf］=6.9×10-4），两者很接近，且对应的允许年失效概率均在1×10-5左右。但是，JCSS 概率模式规范与我国统一标准还有几个重要区别：

（1）JCSS 模式规范规定的是允许年失效概率，是经投资-效益分析获得的“可接受失效概率”或者允许失效概率，再换算得到目标可靠指标。允许年失效概率是一个开放的概念，用来确定不同使用年限下的目标可靠度十分方便，且便于与其他行业的风险概率进行比较分析（各行业的风险概率多采用年失效概率表示）。

（2）我国统一标准规定的目标可靠指标对应于设计使用年限（对一般结构为50 年）内的允许累积失效概率，是经对我国20世纪70年代的设计规范中各类结构构件的可靠度进行校准后确定的。即经校准并归类统一后得到目标可靠指标，再经换算得到允许累积失效概率。我国规范未规定采用不同设计使用年限时是否可调整目标可靠指标，但文献［11］对结构重要性系数γ0的规定中，除因结构的破坏后果严重性不同用γ0对目标可靠度进行调整外，对设计使用年限为100 年及以上和 50 年的结构构件，其γ0也分别取 1.1 和 0.9；而在文献［12］中，采用考虑设计使用年限的调整系数γL对可变荷载进行调整。这两种方法有所不同，但实质上均调整了结构构件的目标可靠度。

（3）JCSS 模式规范按照“采取安全措施的费用”分为三个等级，并可根据不同的不确定性程度、质量保证和定期检查措施、使用年限等对目标可靠指标进行相应的调整。这个规定对我国制定既有结构评定的目标可靠度分级标准有非常重要的借鉴意义。

总之，对于设计使用年限为50 年的一般建筑结构构件，JCSS 模式规范与我国统一标准规定的目标可靠指标比较接近，其对应的允许年失效概率均在1×10-5左右，但JCSS 模式规范采用的允许年失效概率的概念开放性更好，用其来确定既有结构可靠性评定的目标可靠指标十分方便。

2 基于评估使用年限的目标可靠度

2.1 基本思路

上述比较表明，JCSS 概率模式规范与我国统一标准采用的目标可靠度参数不同，参数的来源及依据不同，参数的开放性也有差异。本文将以我国统一标准规定的目标可靠度为基准，利用JCSS 概率模式规范中的允许年失效概率概念，建立基于评估使用年限的目标可靠度，并探讨结构构件的使用安全寿命准则。

既有结构的抗力不断退化且退化速率越来越大，这是不利的一面，但另一方面，人们对一般建筑的期望使用年限越来越短，这又是有利的一面。如何综合平衡这两个方面，建立既有结构的目标可靠度，综合发挥既有结构的潜在价值，达到可持续利用的目标？作者提出如下的思路：

一般而言，通过加固措施提高结构构件的可靠度，其经济代价远大于新建结构设计，装修修复等间接费用较大，而且还会对其正常使用造成较大影响，因此既有结构可靠性评定应贯彻“最小结构处理”原则［1，13］。另一方面，对既有结构进行周期性检测评定和维修，可通过现场检测降低设计中隐含的某些参数的不确定性，对其后续使用条件进行限定，通过缩短评估使用年限降低后续使用年限内的结构抗力退化程度，通过检查维修发现并处理某些安全隐患等，这些措施可不同程度降低抗力和荷载效应的不确定性，从而提高结构的可靠度，降低安全风险。即检测评定和维护的周期越短，结构安全风险越低，可靠性越好。基于这些因素，JCSS 概率模式规范对既有结构评定允许采用低于一般新建结构设计的目标可靠指标（即表2中的A类要求）。

我国统一标准对设计使用年限为50 年的一般结构构件规定了目标可靠指标，这个目标可靠指标对应于50 年内的允许累积失效概率，这是我们确定既有结构评定的目标可靠度的基准。当既有结构评定采用低于原设计使用年限的评估使用年限时，以评估使用年限内的允许累积失效概率与原设计使用年限内的允许累积失效概率相等为原则，就可获得对应于不同评估使用年限的允许年失效概率，据此可确定目标可靠度要求。

2.2 评估使用年限缩短时的允许失效概率和目标可靠指标

设结构构件的原设计使用年限为T0=50 a，可靠性评定时采用的评估使用年限为T≤T0，则根据评估使用年限内的允许累积失效概率与原设计使用年限内的允许累积失效概率相等的原则，有

式中，［Pf，T（T）］为评估使用年限T内的允许累积失效概率；［Pf，50（50）］为原设计使用年限50 年内的允许累积失效概率。

根据文献［3-4］，当结构抗力在使用年限内不退化时，结构的累积失效概率与服役年数成正比，则有

式中，［Pf，1（50）］和［Pf，1（T）］分别为设计使用年限50年和评估使用年限T内的允许年失效概率。

由式（1）-式（3）可得

可见当评估使用年限T小于原设计使用年限50 年时，其允许年失效概率增大。由于我国规范的荷载统计参数均是按设计基准期50 年获得的，将允许年失效概率换算为设计基准期50 年内的允许失效概率：

式中，［Pf，50（T）］为评估使用年限缩短为T时，在设计基准期50 a内的允许累积失效概率换算值。

［Pf，50（T）］对应的目标可靠指标［β50（T）］为

其中，Φ-1（·）为标准正态分布函数的反函数。

我国统一标准规定了设计使用年限为50 年的一般结构构件的目标可靠指标［β50（50）］，对延性破坏和脆性破坏构件分别为3.2 和3.7，其对应的50年内的允许累积失效概率［Pf，50（50）］分别为0.000 69 和0.000 11。根据式（5）和式（6）计算的［Pf，1（T）］、［Pf，50（T）］及其对应的目标可靠指标见表3。

表3 不同评估使用年限下的允许失效概率、目标可靠指标与抗力需求折减系数Table 3 Allowable failure probability，target reliable index and resistance demand discount coefficients under different assessed service life

2.3 评估使用年限缩短时的抗力需求折减系数

当抗力R和荷载效应S均为正态分布时，结构的可靠指标为

式中：μR和μS分别抗力和荷载效应的平均值；σR和σS分别抗力和荷载效应的标准差。

为给出抗力需求折减系数λR（T）的近似建议值，假定评估使用年限缩短为T时，抗力的平均值减小为μR（T）而标准差保持不变，则结构可靠指标β（T）为

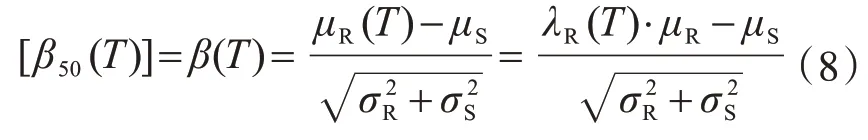
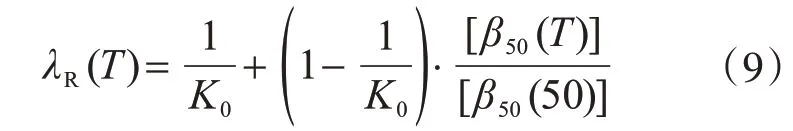
中心安全系数K0的统计值见文献［3］，按式（9）计算的抗力需求折减系数λR（T）见表3，并给出λR（T）建议值。

2.4 本文与文献[3]的两种抗力需求折减系数分析方法比较

图1 给出不同评估使用年限时的累积失效概率增长曲线（不考虑抗力退化）。现根据图1 对本文和文献［3］两种抗力需求折减系数分析方法进行比较。

本文求解抗力需求折减系数的方法如下：当不考虑抗力退化时，按50 年设计的结构的累积失效概率随使用年限的增长而线性增大。当评估使用年限由50 年缩短为T年时，由图中的PA根据“按50年设计增长线”线性折减得到PB，再根据不同评估使用年限内的允许累积失效概率相等原则得到PB’=PA，由于需直接采用设计基准期50 年内的荷载统计参数，将PB’根据“按T 年评估增长线”线性扩大得到PA’，最后根据PA和PA’对应的目标可靠指标按式（10）计算得到抗力需求折减系数：

文献［3］求解抗力需求折减系数的方法如下：当评估使用年限由50 年缩短为T年时，可由图1中PA和PB对应的目标可靠指标按式（11）计算得到荷载效应折减系数λS（T），又根据不同评估使用年限内的允许累积失效概率相等原则得到PB’=PA，故可直接根据PB’和PB对应的目标可靠指标按式（12）计算得到抗力需求折减系数λR（T）：

图1 不同评估使用年限时的累积失效概率增长曲线Fig.1 Cumulative failure probability growth curves for different assessed service life

文献［3］的抗力需求折减系数即是以式（11）、式（12）计算得到的。

由上述分析可知，本文和文献［3］两种方法在分析过程中均采用了不同评估使用年限内的允许累积失效概率或目标可靠指标相等的原则。本文的抗力需求折减系数是根据图1 中两条增长线上横坐标为50a 的允许累积失效概率对应的目标可靠指标之比βA’/βA计算得到的，而文献［3］的抗力需求折减系数是根据图1 中两条增长线上横坐标为T的允许累积失效概率对应的目标可靠指标之比βB’/βB计算得到的，虽然两者的允许累积失效概率之比相等，但其对应的目标可靠指标之比有一定差别（见表3 中“［β50（T）］／［β50（T）］”列数值比较），故计算得到的抗力需求折减系数在数值上也有一定差别。表3 列出了两种方法计算结果的比较，可见，本文方法计算的抗力需求折减系数略小于文献［3］方法计算值，即文献［3］方法计算结果略偏安全。为了避免两种方法产生不同效果，最后给出的抗力需求折减系数建议值相等。显然，相对于文献［3］的方法，本文方法避免了荷载效应折减系数的求解，计算更加简便，也更容易理解。

按T年评估时和按50 年设计时的累积失效概率增长曲线不同，其本质是前者的斜率（增长速率）大于后者，即前者的允许年失效概率［Pf，1（T）］大于后者的允许年失效概率［Pf，1（50）］。也就是说，在不同评估使用年限内的允许失效概率相等的原则下，目标可靠度的本质区别是其对应的允许年失效概率不同。

3 关于危险构件的定义和既有结构构件的使用安全寿命准则

3.1 关于危险构件的可靠度定义

我国《城市危险房屋管理规定》（建设部令第129 号）规定：危险房屋系指结构已严重损坏或承重构件已属危险构件，随时有可能丧失结构稳定和承载能力，不能保证居住或使用安全的房屋。同时又规定，经鉴定属危险房屋的，鉴定机构必须及时发出危险房屋通知书；属于非危险房屋的，应在鉴定文书上注明正常使用条件下的有效时限，一般不超过1 年。这里虽未定义危险构件，但明确定义了危险房屋具有“随时”危及居住或使用安全的危险特性，同时，规定了这种发生危险的“随时”性是以1 年为时限的。这可以理解为，危险房屋鉴定的评估使用年限可取1年。

现行《危险房屋鉴定标准》（JGJ 125—2016）［14］将危险房屋定义为“房屋结构体系中存在承重构件被评定为危险构件，导致局部或整体不能满足安全使用要求的房屋”，将危险构件定义为“承载能力、连接构造等性能及裂缝、变形、腐蚀或蛀蚀等损伤指标不能满足安全使用要求的结构构件”。这两个定义虽然采用了更多的描述性语言，但反而没有《城市危险房屋管理规定》的定义和规定明确。文献［14］规定，对于主要结构构件，当承载力不满足φR/（γ0S）≥0.9 时即评为危险构件（其中φ为不同建造年代的调整系数）。这里暂不讨论采用调整系数φ的合理性，其阈值0.9 与《民用建筑可靠性鉴定标准》（GB 500292—2015）［6］中d级构件相同，其对应的可靠指标取为β0-0.5，即相当于设计使用年限为5 年的结构构件的目标可靠指标。显然，这个目标可靠指标与危房鉴定的时限（1年）不协调，同时显得偏高。

由于我国标准规定的一般房屋的设计使用年限为50 年，参考我国《城市危险房屋管理规定》的规定将危险房屋鉴定的评估使用年限取1 年时，根据“评估使用年限内的允许累积失效概率与原设计使用年限内的允许累积失效概率相等”的原则，相应危险构件的年失效概率为现行设计标准允许值的50 倍。根据表3，评估使用年限为1 年时，延性构件的目标可靠指标为1.82，比文献［2］规定值降低1.38；脆性构件的目标可靠指标为2.54，比文献［2］规定值降低1.16；相应的抗力需求折减系数一般超过0.83。根据上述分析，本文给出危险构件的通俗定义为：已严重损坏，或安全性严重不符合现行设计标准要求，在极短时间（不超过1 年）内即可能危及使用安全的构件。其可靠度定义为：年失效概率超过现行设计标准允许值的50 倍的构件，其对应的目标可靠指标比现行设计标准的规定值降低1.2 以上，抗力-荷载效应比（抗力需求折减系数）低于0.83。

3.2 既有结构构件的使用安全寿命准则

《混凝土结构耐久性评定标准》（CECS 220：2007）［15］对钢筋混凝土构件确定三种耐久性极限状态：钢筋开始锈蚀，钢筋保护层锈胀开裂，混凝土表面出现可接受的最大外观损伤。显然，这里的耐久性极限状态是限定在正常使用极限状态范畴的。本文讨论的既有结构构件的使用安全寿命准则，则属于承载能力极限状态范畴。

经典的可靠性理论［16］中均有失效概率密度、可靠度、累积失效概率（不可靠度）、失效率和可靠寿命等重要概念。如果研究的随机变量是产品的寿命T，其失效概率密度函数为f（t），则其累积失效概率函数（也称不可靠度函数）F（t）和可靠度R（t）分别为

失效率h（t）定义为产品工作到t时刻未失效的条件下，在下一短暂时间间隔内发生失效的概率，即

可靠度等于给定值r时的寿命称为可靠寿命：

其中，可靠度r=0.5 时的可靠寿命T0.5又称为中位寿命。

可见，用失效率的概念容易给出产品的可靠寿命。对既有结构构件而言，由于其允许的累积失效概率很小，可靠度R（t）的数值接近1.0，故由式（15）可知h（t）≈f（t），即年失效率与年失效概率接近。因此，既有结构构件的使用安全寿命定义为：结构构件的年失效率下降为现行设计标准允许值的50 倍时的累积服役时间。用通俗语言也可将使用安全寿命定义为：既有结构构件由于可靠度降低成为危险构件时的累积服役时间。

4 算例分析

文献［4］以某钢筋混凝土梁为例对其受弯承载力的可靠度进行了分析。本文仍以该钢筋混凝土梁为例进行分析，主要参数取值见文献［4］。下面仅分析抗力中等退化程度一种工况，其抗力衰减函数为

系数α取 0.000 4。按式（17），φ（50）=0.9，φ（100）=0.6，即服役年数为 50 年和 100 年时，抗力退化率分别为0.9和0.6。

按文献［3-4］，计算年失效概率及其对应的可靠指标时，由于时段长度1 年很短，抗力退化系数近似取该评估时段结束时刻的值。可靠度分析采用JC法，可变荷载（风荷载）采用1年的统计参数，将分析得到的实际可靠指标按标准正态分布函数换算为实际年失效概率。图2 给出了实际年失效概率的变化规律及其允许值，其中纵坐标是对数坐标。图3 给出了与年失效概率对应的可靠指标变化规律及其目标值。年失效概率的允许值和可靠指标的目标值按表3 中“延性破坏构件”一栏取值。

图2 年失效概率的变化规律Fig.2 Change rule of annual failure probability

图3 与年失效概率对应的可靠指标的变化规律Fig.3 Change rule of reliable index corresponding to annual failure probability

由图2 可见，年失效概率曲线Pf，1（t）与T=50年、T=30 年、T=20 年、T=10 年、T=5 年、T=1 年对应的允许年失效概率［Pf，1（T）］的交点横坐标分别为t=16 年、t=32 年、t=41 年、t=53 年、t=63 年、t=80年。这说明，当结构服役30 年时对其进行第一次安全性检测评定，评估使用年限取10 年；在服役40 年时再按评估使用年限10 年进行第二次检测评定，此时t=30+10+10=50 年，即服役刚满原设计使用年限50 年。此后如仍需继续服役，则按评估使用年限5年再进行两次检测评定，至t=50+5+5=60 年。在此之前，结构的失效概率和评估周期尚控制在正常范围，只需进行4 次检测评定，无需采取结构加固或专门的耐久性防护措施，只要对其正常维护保证其正常使用功能，则该结构构件可安全服役60 年。此后若需继续服役，应每隔1 年进行一次检测评定（评估使用年限为1 年），此时结构构件的可靠性仅维持在较低水准，未构成“危险构件”而已；直至服役到80 年时，结构构件达到使用安全寿命终点，此后的年失效概率超过现行设计标准的50 倍以上，已属于不可接受失效概率，必须采取加固措施。根据图3 所示可靠指标变化规律及其与目标可靠度的对比，也可得到相同的结论。

图4 给出抗力衰减系数φ(t)及其与抗力需求折减系数λR（T）的比较（假定R0/S0=1.0）。图中的抗力需求折减系数按式（9）计算（计算时取本例中心安全系数的实际值K0=1.97）。根据图4 也可分析得到与可靠度方法基本一致的结论，但上述抗力衰减系数-抗力需求折减系数比较法所得结果相对偏保守（偏安全）。

图4 抗力衰减系数及其与荷载效应折减系数的比较Fig.4 Resistance degradation coefficient and its comparison with load effect discount coefficient

上述过程完整体现了对结构进行周期性检测评定的作用和意义。应该指出，上述分析结论在只考虑耐久性对构件承载能力影响、日常维护不改变抗力退化程度和速率的假定下才成立，而且是在设计阶段作出的保守的预测分析。一般而言，当结构构件的抗力退化率超过一定程度后，对其正常使用功能会产生影响，故服役一定时间后，应对其采取耐久性修复措施方可满足正常使用要求，或者直接采取加固措施提高其安全性。当对结构构件采取耐久性修复或加固措施后，其在后续服役期内的实际失效概率降低，实际可靠指标提升，此时结构检测评定的周期可延长。

5 结 论

（1）我国统一标准规定的目标可靠指标来自对20世纪70年代设计规范的可靠度校准，对应于设计使用年限内的允许累积失效概率；而JCSS 模式规范直接规定了允许年失效概率及其对应的目标可靠指标。对于设计使用年限为50 年的一般建筑结构构件，两者的目标可靠度比较接近，其对应的允许年失效概率均在1×10-5左右，但JCSS 模式规范采用的允许年失效概率概念开放性更好。

（2）本文以我国统一标准规定的目标可靠度为基准，以评估使用年限内的允许累积失效概率与原设计使用年限内的允许累积失效概率相等为原则，计算得到对应于不同评估使用年限的允许年失效概率。将不同评估使用年限的允许年失效概率换算为设计使用年限50 年内的目标可靠指标，并提出了抗力需求折减系数建议值。

（3）以允许年失效概率为依据，提出了危险构件的可靠度定义和既有结构构件的使用安全寿命准则。

（4）以某锈蚀钢筋混凝土梁的受弯承载力分析为例，采用可靠度方法和抗力衰减系数-抗力需求折减系数比较法研究了其使用安全寿命、检测评定周期等。