体感交互虚拟漫游的沉浸感评价

周 强，张敏雄，吴新丽，李 昕，黄金鹏，杨文珍，潘志庚

体感交互虚拟漫游的沉浸感评价

周 强1，张敏雄1，吴新丽1，李 昕1，黄金鹏1，杨文珍1，潘志庚2,3

(1. 浙江理工大学虚拟现实实验室，浙江 杭州 310018；2.杭州师范大学数字媒体与人机交互研究中心，浙江 杭州 311121；3. 广州玖的数码科技有限公司，广东 广州 510623)

沉浸感是虚拟漫游的重要特征，目前体感交互的虚拟漫游存在严重的感知失真问题，虚拟场景运动的视觉感知与人机交互的体感感知不能相互匹配，破坏了虚拟漫游的沉浸感。基于Catmull-Rom曲线的非等距插值算法、等距插值算法和实时插值算法，分别构建3种不同的虚拟漫游路径，评价体感交互虚拟漫游的沉浸感。主观评价实验和仿真实验的结果表明：Catmull-Rom曲线的非等距插值漫游路径，无论是匀速漫游还是变速漫游，均存在明显的感知失真现象；基于Catmull-Rom曲线的等距插值漫游路径适用于匀速漫游，但不太适合用于变速漫游；基于Catmull-Rom曲线的实时插值漫游路径能实现真实运动速度与场景运动速度的匹配，较好地解决虚拟漫游时视觉感知与身体运动感知不一致的问题，增强了虚拟漫游的沉浸感。

虚拟漫游；体感交互；Catmull-Rom曲线；漫游路径；沉浸感评价

虚拟漫游能让用户游览虚拟世界，获得身临其境的沉浸感和人机互动的趣味性。传统的虚拟漫游通常是指人们通过鼠标、键盘等交互设备，用手指输入交互指令，游览虚拟场景。近年来，人们研发了各种体感交互设备[1-4]，进行虚拟漫游，包括虚拟驾驶、虚拟骑行、虚拟太空旅游等，极大拓展了虚拟漫游的应用领域。这类新型漫游形式通常需要用户的身体参与人机交互并感受虚拟场景反馈的信息，可以统称为体感漫游。比如，虚拟骑行是以自行车为交互设备[5]，用户以真实的速度在虚拟场景中骑行，通过体感察觉到身体运动，通过视觉观察到虚拟场景运动，达到健身和娱乐的目的。

然而，体感漫游存在着感知失真问题，降低了用户的体验感。在体感漫游过程中，如果身体感受到的运动信息与场景反馈的视觉信息不同步，就会产生体感不一致的现象，即体感失真。此时，用户无法获得在现实世界中运动的感觉，影响了虚拟环境的沉浸感和真实性。这种运动状态与视觉状态不一致的体感失真对虚拟现实晕动症有很大的影响，用户的晕动症程度会随着真实运动状态与视觉一致性的减小而提升，在极端条件下可产生用户无法承受的生理不适状况[6-7]。VR健身单车的晕动症测试表明：虚实运动体感不一致更容易产生晕动症，其主要症状产生的先后顺序为头胀、视觉模糊、头晕、视觉疲劳(眼花)和恶心感[8-9]。

通过体感漫游的实际应用[10]，总结出3种虚实运动体感不一致现象：即启停、匀速、变速运动体感不一致。①启停运动体感不一致是指虚拟场景的运动不能实时匹配用户身体启动或停止运动的现象，有明显的滞后感，如用户已停止骑车，但场景还继续向前运动，或者用户已开始骑车，但场景却不移动。②匀速运动体感不一致是指虚拟场景的运动速度不能匹配用户身体感知到的实际匀速运动速度，如用户在匀速骑行，但视觉上却感觉场景的运动速度时快时慢。③变速运动体感不一致是指虚拟场景的运动速度变化率不能匹配用户身体感知到的实际运动速度变化率，如用户正在加速骑车，但是视觉上却感觉不到场景在加速运动。

在虚拟漫游系统能够实时获取用户运动数据并渲染虚拟场景的条件下，本文研究发现漫游路径的生成是引起体感不一致性的重要因素。目前，漫游路径主要是由曲线插值算法生成[11-14]，包括Bezier曲线、Hermite曲线和Catmull-Rom曲线等插值算法。Bezier曲线插值算法灵活性强，能够拟合出复杂的曲线，已用于虚拟漫游的路径生成[15-16]。然而，在Bezier曲线插值算法生成漫游路径时，除了要在虚拟道路上放置若干个路径点外，还需在每段Bezier曲线上人工添加2个控制点以调整曲线曲率。由于体感漫游的虚拟道路很长，曲线段数目很多，人工增加Bezier曲线控制点，不仅工作量较大，而且难以保证生成的漫游路径与虚拟道路有较好的重合度。Hermite曲线是由给定起点和终点坐标，以及起点和终点处的切线矢量来确定的一条曲线。若由多段Hermite曲线组成一条虚拟漫游路径，需要给出每段Hermite曲线的起点和终点的切线值[17]。然而，切线值作为曲线参数并不直观，且无法手动调整。相对于Bezier和Hermite曲线，Catmull-Rom曲线[18-19]可以通过曲线上已知的端点，直接拟合出曲线，不需要人工额外增加控制点，减少了工作量，更适用于体感漫游的路径生成。

本文基于Catmull-Rom曲线提出非等距插值算法、等距插值算法和实时插值算法，分别生成体感漫游路径，并开展体感一致性评价的实验，探讨基于Catmull-Rom曲线的插值算法与体感一致性的关系，为解决体感失真问题提供思路。

1 Catmull-Rom曲线非等距插值的漫游路径

在虚拟漫游系统中，漫游路径通常是由已知路径点(或称控制点)，经曲线插值算法生成。漫游路径由多段曲线组成，在每段曲线上有若干个插值点。

1.1 Catmull-Rom曲线插值

Catmull-Rom曲线由4个连续控制点确定，且控制点均在曲线上(图1)。在已知曲线上4个点的情况下，Catmull-Rom曲线只能计算出1和2点之间的插值点，即Catmull-Rom曲线不经过首尾2个点[20-21]。

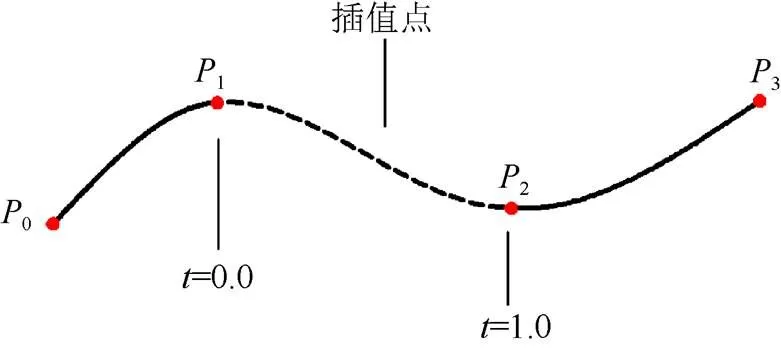
图1 Catmull-Rom曲线

图1中，1，2，3，4为Catmull-Rom曲线上的控制点。已知1，2，3，44个路径点，由Catmull-Rom曲线插值公式，可以求得12路径上的插值点，得到其漫游路径，即

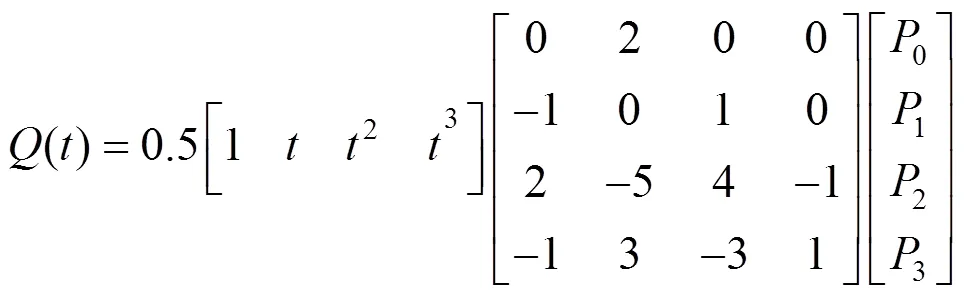
其中，为插值参数；()为插值点坐标。若要在12路径上获得个插值点，值可以从1/，2/，3/，4/依次递增至1，当=0时，插值点位于点1处，当=1时，插值点位于点2处。

1.2 Catmull-Rom曲线非等距插值漫游路径

式(1)只能求得1，22个路径点之间的插值点，不能生成经过首尾路径点0，3的的漫游路径。为此，本文添加2个辅助点，以便Catmull-Rom曲线穿过首尾路径点，生成整条漫游路径。已知虚拟道路有1,2,···P(≥4)路径点，可构建出首尾2个辅助点0和P+1，其中，0=21–2， P+1=2P–P–1。则插值公式为

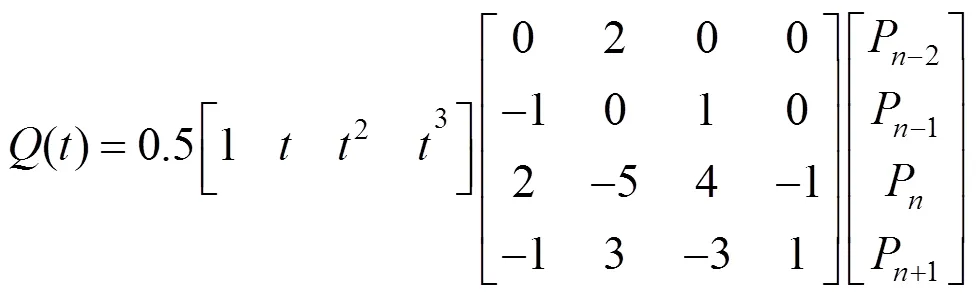
令：

=2P–1，=P–P–2

=2P–2–5P–1+4P+P+1

=–P–2+3P–1–P+P+1

式(2)可以化简为

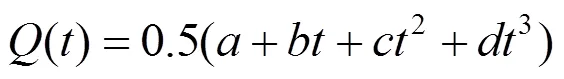
因此，只需利用已知的路径点，就可以由式(3)生成整条漫游路径。在生成漫游路径时，直线段通常只需2个路径点，曲率较大的曲线段则需要布置多个路径点，以保证生成的漫游路径与虚拟道路有较好的重合度。然而，式(3)会在2个路径点之间生成相同个数的插值点，这会使得曲率较大曲线段处有更多插值点。如图2所示，相同距离下，曲线段比直线段的插值点更多。

在虚拟漫游时，视点会沿着漫游路径从一个插值点依次移动到下一个插值点。当距离间隔相同时，沿着Catmull-Rom曲线非等距插值漫游路径匀速运动时，会觉得直线段漫游速度要比曲线段漫游速度快，感受到运动失真。为此，需要改进Catmull-Rom曲线插值算法，以生成等距插值的漫游路径。

2 基于Catmull-Rom曲线等距插值的漫游路径

在一条虚拟路道上，如果路径点是均匀布置的，通过式(3)可以生成等距插值的漫游路径，但是，人工很难放置出均匀的路径点。本文提出一种基于Catmull-Rom曲线的等距插值算法，生成插值点均匀分布的的漫游路径。在已知插值点总数目的条件下，基于Catmull-Rom曲线等距插值算法的核心是求出曲线总长度，然后根据距离进行插值，使得插值点之间的长度相同。要根据距离进行曲线插值，首先要获取曲线段的长度；然后计算出点在曲线上的位置。已知根据参数可计算曲线上插值点的位置坐标。因此只要找出曲线长度与参数的关系，即可获得某长度下插值点的位置坐标。在Catmull-Rom曲线算法中，为插值参数，而根据距离插值，需要将弧长也作为参数。因此等距插值的重点在于弧长参数化。

2.1 Catmull-Rom曲线长度求解

从数学模型角度，式(3)可以看作是时间处位置为()的粒子的路径。求出粒子在处的速度函数()，将()在Î[min,max]上积分，可以获得2个值之间的弧长，由此获得弧长与曲线参数的函数()，即

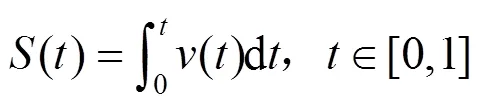
若=1，()为曲线总长度。

2.2 基于曲线长度的插值点坐标求解

将曲线均分为份，每份距离为/，将/，2/，···，代入()中，可求得每份距离对应的值。并通过牛顿迭代法求出的近似解，设()=()–(0≤≤)，为弧长，求出值，使得()=0。

由牛顿迭代法可得

将(t)=(t)–代入式(6)

(7)

迭代起始值可以设置为弧长与曲线总长度的比值

设置迭代误差和迭代次数，将t值代入式(7)进行迭代，可以求出t+1的近似解。

牛顿迭代可能会出现错误解的情况，主要原因如下：由于()=()≥0，可知()是非递减函数。如果在Î[0,1]上，()≥0，则()为凸函数，牛顿迭代收敛，在Î[0,1]上一定有解。但在Î[0,1]上，()可能为负值，导致牛顿迭代的解在Î[0,1]之外。为了避免在的定义域之外进行迭代，可将牛顿迭代法和二分法结合，求解值，如图3所示。按图3流程获得的值后，将值代入式(3)，获得对应的插值点的坐标。

2.3 基于Catmull-Rom曲线的等距插值

假设有一条漫游路径，其点为1,2,···,P，辅助点为0，P+1，则基于Catmull-Rom曲线等距插值的过程描述如下(图4)：

图3 求解t的流程图

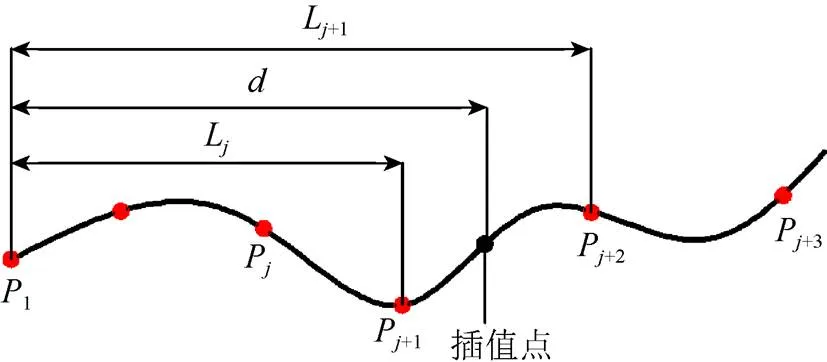
图4 Catmull-Rom曲线的等距插值

(3) 将整条漫游路径均匀划分为份，即在漫游路径上添加个插值点，每个插值点据曲线起始点1的距离依次为

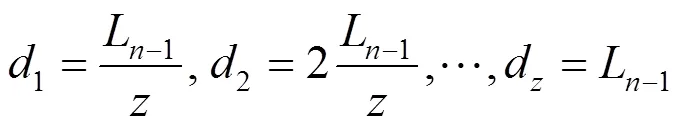
其中，S为插值点距离P+1点的弧长；为插值点据曲线起始点1的距离；L为插值点之前的曲线段累加长度。

(6) 求得插值点的坐标值，即

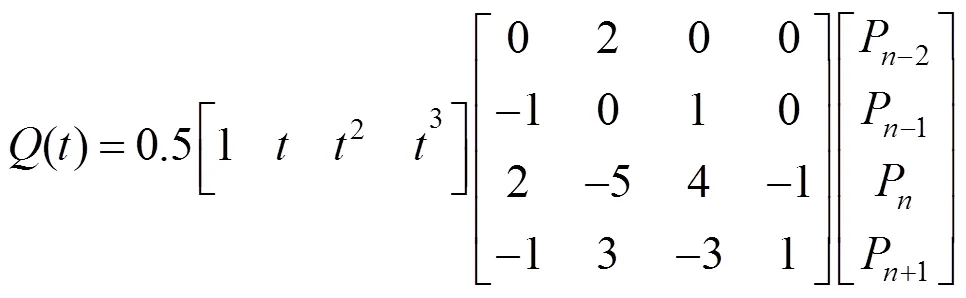
通过上述步骤，可以求得均匀布置的插值点，实现在整条漫游路径上的均匀插值，生成等距插值的漫游路径。在相同时间间隔情况下，人们沿着Catmull-Rom曲线等距插值漫游路径匀速运动时，就不会觉得直线段漫游速度比曲线段漫游速度快，可以感受到虚拟场景的匀速运动。

3 基于Catmull-Rom曲线实时插值的漫游路径

无论是非等距插值还是等距插值，虚拟漫游系统需要预先计算出大量插值点，并且漫游过程中涉及多个插值点的计算，增加了虚拟漫游系统的开销。本文提出了一种基于Catmull-Rom曲线的实时插值算法，可动态生成漫游路径。

假设虚拟漫游系统记录当前帧用户已经漫游的距离为S(即用户在整段漫游路径上已经走过的弧长)，并接收到用户的速度数据为V，那么下一帧漫游的总距离为

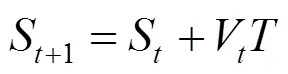
其中，为虚拟漫游系统2帧之间的时间间隔。

由2.3节中的第(4)步，可以判断出插值点位于哪段曲线，将S+1代入式(9)中，可得

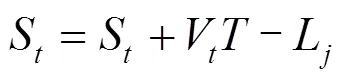
其中，S为当前漫游位置在本段曲线的弧长。

由2.3节中的第(5)和(6)步，可以求得下一帧插值点的坐标值。在下一帧函数执行时，视点(Camera)直接移动到此位置，实现实时插值，动态生成漫游路径。

通过上述方法，可以实时获得用户的漫游位置，要实现虚拟漫游，还需要实时更新用户的视角。通过让用户对着某段时间后用户应该在的位置，获得用户的当前视角。

4 体感漫游一致性评价实验

虚拟骑行是一种典型的体感漫游，通过开展虚拟骑行的体感一致性评价实验，探讨基于Catmull-Rom曲线插值算法与体感一致性的关系。

4.1 实验环境的构建

虚拟骑行体感漫游实验环境主要由动感单车模块、蓝牙通讯模块和虚拟骑行场景模块组成。动感单车模块通过光电测速传感器以200 Hz的采样频率，获取用户的骑行速度，经蓝牙通讯模块j将速度数据传输给虚拟骑行场景。虚拟骑行场景运行在Windows 7操作系统的Boxx (3DBOXX 8500)工作站上，通过巴可Galaxy NW-12投影机，呈现在2.7 m×0 m的环形屏幕中，如图5所示。工作站能够实时渲染虚拟场景。

图5 虚拟骑行的实验环境

图6 虚拟骑行的道路模型

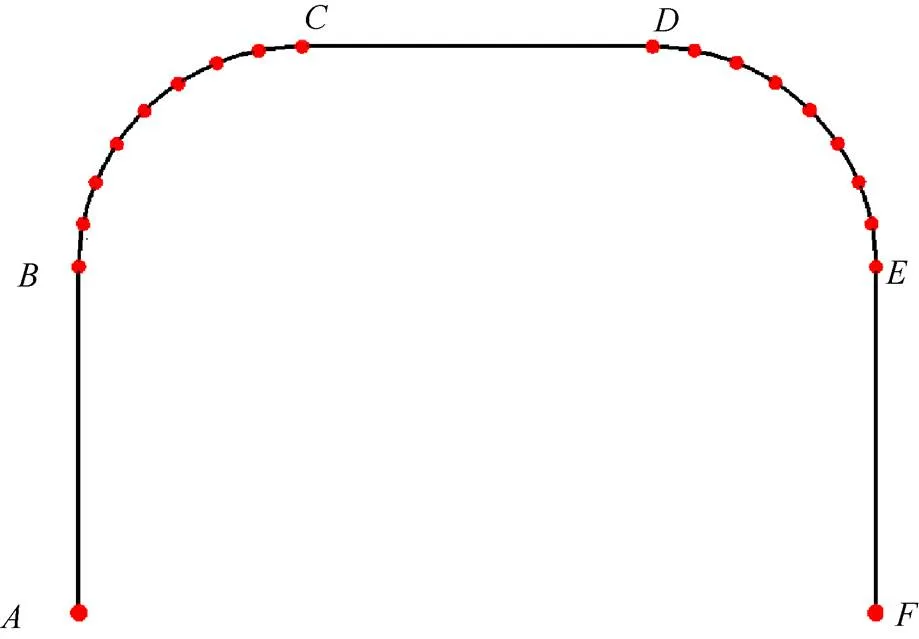
图7 虚拟道路上的路径点

4.2 体感一致性的主观评价

运用Catmull-Rom曲线的非等距插值算法(插值点分别为10，20，40，100个)、等距插值算法(插值点分别为10，20，40，100个)和实时插值算法，分别生成9条虚拟骑行的漫游路径。实验人员由50名身体健康人组成，其中男性30名，女性20名，年龄16~62岁；有骑车经验且非专业运动员，志愿参加虚拟骑行体验。其事先不知道是哪个算法生成的漫游路径，也不知道有多少个插值点。每位实验人员要在每条漫游路径上重复骑行5次，共45次的虚拟骑行体验。

本文要求在每次体验过程中实验人员要有意识地控制骑车速度，分别进行匀速骑行和变速骑行，并完成体感一致性问卷调查，结果见表1。

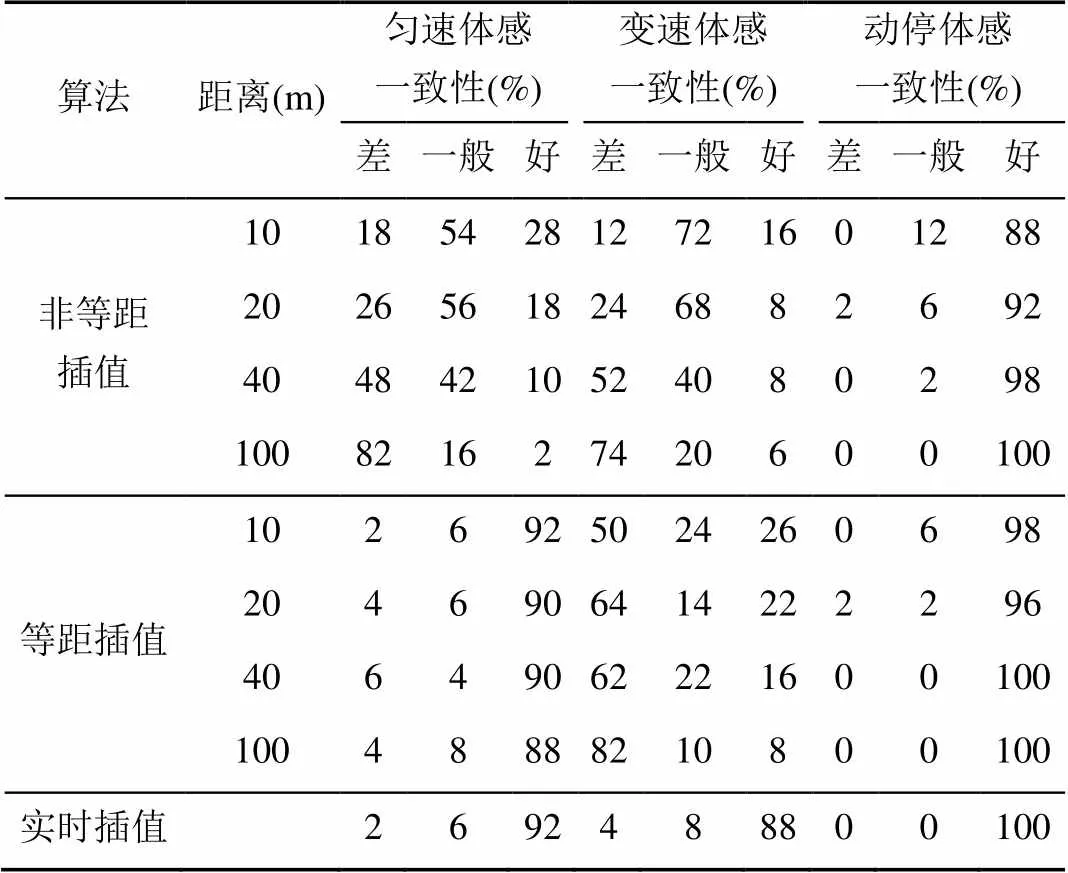
表1 体感一致性的主观评价结果

从表1中得出：①动停体感一致性与漫游路径的生成算法基本无关；②无论是匀速骑行还是变速骑行，非等距插值漫游路径的体验效果不佳；③无论是匀速骑行还是变速骑行，实时插值漫游路径的体验效果比较好；④对于等距插值的漫游路径，匀速骑行的体验效果较好，变速骑行的体验效果很一般。

所有参与实验人员，事先不知道是哪个算法生成的漫游路径，在非等距插值漫游路径的体验过程中，有人反应在匀速骑行时，直道比弯道的骑行速度要快一些；在等距插值的体验过程中，有人反应在变速骑行时，视觉上感受不到场景也在变速运行；在实时插值的体验过程中，有人反应在快速骑行时，场景有时会抖动不够连续。

4.3 非等距插值漫游路径的仿真实验

在Windows 7操作系统的PC机(i7-4700MQ@ CPU 2.40 GHz，16.0 GB)上，开展非等距插值漫游路径的仿真实验，设置视点以10 m/s的均速运动，记录各段曲线段的漫游时间，见表2。

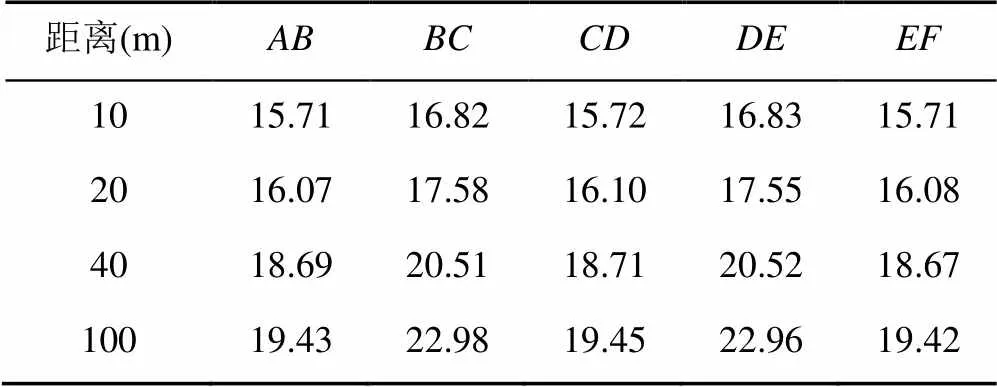
表2 非等距插值各曲线段的漫游时间(s)

由表2可以得到，直线段与曲线段的平均漫游时间，见表3。

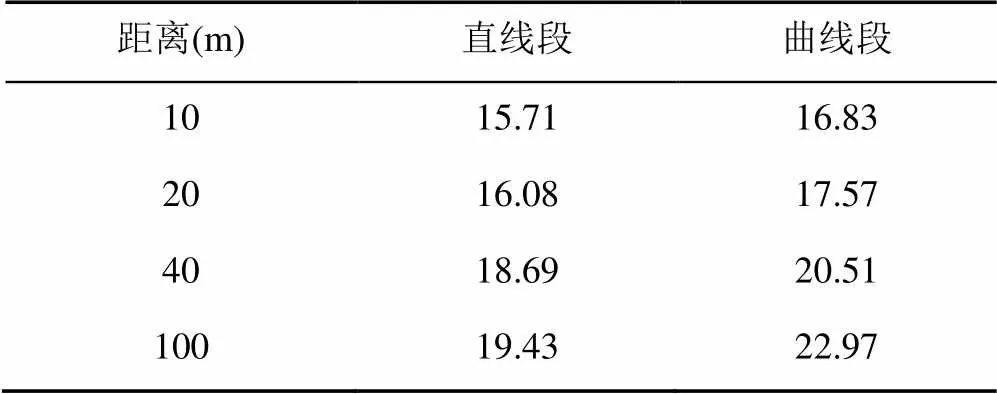
表3 非等距插值直线段与曲线段漫游的平均时间(s)

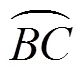
经分析，本文通过视点函数更新视点的位置和方向实现虚拟漫游，视点函数的执行会消耗一定的时间。在漫游过程中，视点沿着曲线的插值点依次移动，即每2个插值点均需要执行一次视点函数以更新位置与方向。因此插值点越多，函数执行的次数越多，所需要的计算时间越多，这会造成插值点较少的直线段比插值点较多的曲线段漫游时间更少。

4.4 等距插值漫游路径的仿真实验

在开展等距插值漫游路径的仿真实验，设置视点以10 m/s的均速运动，记录各段曲线段的漫游时间，见表4。

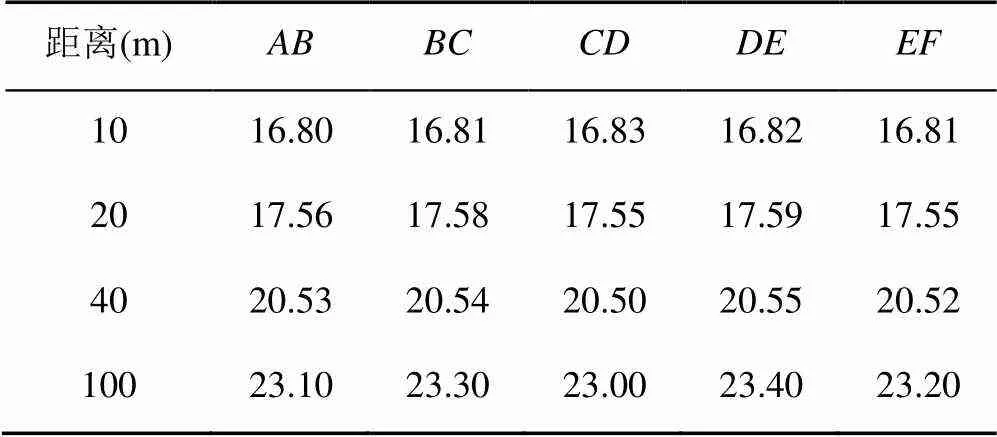
表4 等距插值各曲线段的漫游时间(s)

由表4可知：①在相同插值点个数下，相同距离的直线段和曲线段的漫游时间相同；②随着插值点个数的增加，相同距离所需的漫游时间增长。

进而，在每段曲线上均匀插入4 000个插值点，以不同的速度进行漫游，记录各段曲线段的漫游时间，见表5。

表5 不同速度下等距插值各曲线段的漫游时间(s)

从表5可以发现，在插值点数量较多时，当漫游速度提高到一定时，继续加速，相同距离需要漫游时间并没有明显减少。此时，真实骑行加速与场景运动加速不匹配，会出现变速体感不一致现象。

原因在于将曲线运动转为点与点之间的直线运动需要一定的计算时间，当骑行速度过快时，在漫游路径上会经过更多的插值点，计算时间也会更多，最后会多于一帧所需要的时间。即骑行速度达到一定速度后，由于PC计算能力的限制，一帧的时间最多只能计算这么多插值点，继续加速，一帧的时间，能到达的距离没有太大的变化，这时速度对漫游前进距离的影响就很小了。此时影响虚拟漫游速度的主要为插值点数目，当插值点过多时，虚拟漫游速度会很慢。

5 总 结

体感漫游是近年来出现的一种新型虚拟漫游，存在着感知失真问题，会导致严重的晕动症，用户的体验感差，制约了其在娱乐、旅游和军事等行业的应用。在Catmull-Rom曲线的非等距插值算法的基础上，本文提出了基于Catmull-Rom曲线的等距插值算法，能够实现匀速运动体感一致；本文提出了基于Catmull-Rom曲线的实时插值算法，能够实时动态地生成漫游路径，满足虚拟漫游体感一致性的需求，用户有较好的体验感，提升了虚拟漫游的沉浸感。

通过实验分析得出：Catmull-Rom曲线的非等距插值漫游路径，无论是匀速漫游还是变速漫游，存在明显的体感失真，特别是在插值点较多的情况下，场景运动速度与实际漫游速度的匹配程度更低，体感不一致的现象更为突出；基于Catmull-Rom曲线的等距插值漫游路径能够用于匀速的体感漫游，但是在变速漫游时，插值点个数不能太多，否则会出现变速体感不一致的现象；基于Catmull-Rom曲线的实时插值漫游路径能够用于匀速漫游和变速漫游，但是在高速度的虚拟漫游时，可能会出现场景不连续现象，需要提高虚拟漫游的场景渲染能力加以解决。在实验过程中，测试者感觉到明显的体感不一致会加重晕动症[6,22]，这二者之间的定量化关系有待进一步揭示。

[1] DE FRANCA A C P, SOARES M M. Review of virtual reality technology: an ergonomic approach and current challenges[M]//Advances in Ergonomics in Design. Cham: Springer International Publishing, 2017: 52-61.

[2] MATVIIENKO A, ANANTHANARAYAN S, EL ALI A, et al. NaviBike: comparing unimodal navigation cues for child cyclists[C]//Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems - CHI ’19. New York: ACM Press, 2019: 620.

[3] ARLATI S, COLOMBO V, SPOLADORE D, et al. A social virtual reality-based application for the physical and cognitive training of the elderly at home[J]. Sensors, 2019, 19(2): 261.

[4] PEDROLI E, GRECI L, COLOMBO D, et al. Characteristics, usability, and users experience of a system combining cognitive and physical therapy in a virtual environment: positive bike[J]. Sensors, 2018, 18(7): 2343.

[5] ZHAO J, ABDUL AMIR H F, KHIEW P S. Research and application of device for simulation sports training based on cycle condition[J]. MATEC Web of Conferences, 2017(108): 4013

[6] 蔡力, 翁冬冬, 张振亮, 等. 虚实运动一致性对虚拟现实晕动症的影响[J]. 系统仿真学报, 2016, 28(9): 1950-1956. CAI L, WENG D D, ZHANG Z L, et al.Impact of consistency between visually perceived movement and real movement on cybersickness[J]. Journal of System Simulation, 2016, 28(9): 1950-1956 (in Chinese).

[7] MARTIN-NIEDECKEN A L, ROGERS K, VIDAL L T, et al. ExerCube vs. Personal trainer: evaluating a holistic, immersive, and adaptive fitness game setup[C]//2019 Conference on Human Factors in Computing System. New York: ACM Press, 2019: 88.

[8] 张杨昊, 李孝禄, 许沧粟, 等. 具有运动真实感的VR健身单车设计及测试[J]. 体育科学, 2018(7): 50-55. ZHANG Y H, LI X L, XU C S, et al. Design and test on the VR fitness bike with motion reality[J]. China Sport Science, 2018(7): 50-55 (in Chinese).

[9] KATSIGIANNIS S, WILLIS R, RAMZAN N. A QoE and simulator sickness evaluation of a smart- exercise-bike virtual reality system via user feedback and physiological signals[J]. IEEE Transactions on Consumer Electronics, 2019, 65(1): 119-127.

[10] 李昕, 杨文珍, 周强, 等. 面向虚拟骑行健身的动感单车数据采集系统[J]. 浙江体育科学, 2018, 40(3): 107-111. LI X, YANG W Z, ZHOU Q, et al. Data acquisition system of dynamic bicycle for virtual riding fitness[J]. Zhejiang Sport Science, 2018, 40(3): 107-111 (in Chinese).

[11] KALLMANN M, KAPADIA M. Geometric and discrete path planning for interactive virtual worlds[J]. Synthesis Lectures on Visual Computing, 2016, 8(1): 1-201.

[12] CAILHOL S, FILLATREAU P, FOURQUET J Y, et al. A hierarchic approach for path planning in virtual reality[J]. International Journal on Interactive Design and Manufacturing (IJIDeM), 2015, 9(4): 291-302.

[13] LAVALLE S M. Discrete planning[M]//Planning Algorithms. Cambridge: Cambridge University Press, 2006: 23-62.

[14] BICA A M. Optimizing at the end-points the Akima's interpolation method of smooth curve fitting[J]. Computer Aided Geometric Design, 2014, 31(5): 245-257.

[15] ELHOSENY M, THARWAT A, HASSANIEN A E. Bezier curve based path planning in a dynamic field using modified genetic algorithm[J]. Journal of Computational Science, 2018, 25: 339-350.

[16] CIMURS R, HWANG J, SUH I H. Bezier curve-based smoothing for path planner with curvature constraint[C]//2017 1st IEEE International Conference on Robotic Computing (IRC). New York: IEEE Press, 2017: 241-248.

[17] YOON H S, PARK T H. Motion planning of autonomous mobile robots by iterative dynamic programming[J]. Intelligent Service Robotics, 2015, 8(3): 165-174.

[18] JEROME L. Catmull-Rom curve fitting and interpolation equations[J]. International Journal of Mathematical Education in Science and Technology, 2010, 41(6): 842-849.

[19] YUKSEL C, SCHAEFER S, KEYSER J. Parameterization and applications of Catmull–Rom curves[J]. Computer-Aided Design, 2011, 43(7): 747-755.

[20] DEROSE T D, BARSKY B A. Geometric continuity, shape parameters, and geometric constructions for Catmull-Rom splines[J]. ACM Transactions on Graphics (TOG), 1988, 7(1): 1-41.

[21] CATMULL E, ROM R. A class of local interpolating splines[M]//Computer Aided Geometric Design. Amsterdam: Elsevier, 1974: 317-326.

[22] MITTELSTAEDT J, WACKER J, STELLING D. Effects of display type and motion control on cybersickness in a virtual bike simulator[J]. Displays, 2018, 51: 43-50.

Immersion evaluation of virtual roaming with proprioceptive interaction

ZHOU Qiang1, ZHANG Min-xiong1, WU Xin-li1, LI Xin1, HUANG Jin-peng1, YANG Wen-zhen1, PAN Zhi-geng2,3

(1. Virtual Reality Laboratory, Zhejiang Sci-Tech University, Hangzhou Zhejiang 310018, China; 2. Digital Media & Interaction Research Center, Hangzhou Normal University, Hangzhou Zhejiang 311121, China; 3. Guangzhou NINED Digital Technology Co. Ltd, Guangzhou Guangdong 510623, China)

Immersion is significantly characteristic of virtual roaming. Currently perceptual distortion is a serious problem in virtual roaming with proprioceptive interaction. Thus, the visual perception of virtual scene motion cannot match the somatosensory perception, which undermines the immersion of virtual roaming. The curve non-equidistant interpolation algorithm, isometric interpolation algorithm and the real-time interpolation algorithm were established based on Catmull-Rom curve, so as to carry out the immersion evaluation of virtual roaming with proprioceptive interaction. The results of subjective evaluation experiments and simulation experiments show that the non-equidistant interpolated roaming paths of Catmull-Rom curves had obvious somatosensory distortions both in uniform roaming and in variable-speed roaming. The equidistant interpolation roaming path based on Catmull-Rom curve was suitable for uniform roaming, but unsuitable for variable-speed roaming. The real-time interpolated roaming path based on Catmull-Rom curve can match the real-motion speed with the scene-motion speed, thus solving the inconsistency between the visual perception and body motion perception in virtual roaming. Therefore, the proposed algorithms can improve the immersion of virtual roaming.

virtual roaming; proprioceptive interaction; Catmull-Rom curve; roaming path; somatosensory evaluation

TP 391

10.11996/JG.j.2095-302X.2020030342

A

2095-302X(2020)03-0342-08

2019-12-10；

2020-01-03

广州创新创业领军团队项目(CXLJTD-201609)；浙江省自然科学基金项目(LY20F020019，LQ19F020012，LQ20F020001)；国家重点研发计划项目(2018YFB1004901)；浙江省基础公益研究计划项目(LGF19E050005)

周 强(1996-)，男，浙江余杭人，硕士研究生。主要研究方向为虚拟现实、人机交互。E-mail：2947093807@qq.com

杨文珍(1976-)，男，浙江义乌人，教授，博士，硕士生导师。主要研究方向为虚拟现实、人机交互。E-mail：ywz@zstu.edu.cn