融合FAHP和TOPSIS的适老化产品综合评价与优选方法——以老年智能手环为例

杨 梅，丛扬帆，李雪瑞

融合FAHP和TOPSIS的适老化产品综合评价与优选方法——以老年智能手环为例

杨 梅，丛扬帆，李雪瑞

(山东科技大学艺术与设计学院，山东 青岛 266590)

为了更全面地对适老化智能手环进行综合评价，进而辅助最终的方案评价与优选，从产品设计、用户体验、人机交互和实际生产4个维度构建了适老化智能手环的评价模型。首先采用基于三角模糊数的层次分析法(FAHP)计算出各项评价准则的权重，然后采用逼近理想解排序法(TOPSIS)对若干备选方案做出评价并完成排序，最后根据结果进行方案的综合评价与优选。以某品牌16款适老化智能手环的备选方案为例，证明FAHP-TOPSIS法的可行性，发挥其现实意义。该评价优选方法，在考虑人的思维模糊性的基础上，从系统与层次等多个角度将思维过程进行定性与定量分析，从而为适老化智能手环方案的优选问题提供清晰适合的决策方案与优化思路。

适老化；智能手环；FAHP-TOPSIS法；综合评价；方案优选

近几年，我国老年群体人口基数大、增长速度过快，导致社会老龄化问题持续加深。从调查研究得知，已有较多老年人在使用适老化智能设备，如智能手环监测运动情况，实现智能化的生活健康管理[1]。众多企业抓住老年人智能穿戴产品存在巨大市场潜力这一机遇，开始在适老化手环研发与设计中融入智能化设计理念，主打辅助老年人健康与生活，缓解现代子女的生活压力的概念。

在手环设计阶段，设计师会提出多个方案；在方案决策阶段，企业考虑到市场、成本、技术、资金和时间等客观因素，通常会有一款或几款方案被投入生产，但在这个过程中，并没有较为客观的评估依据，决策者从自身职务的角度出发，并结合个人观点进行评价，易造成最佳设计方案的误选或漏选，给企业造成不必要的经济损失。因此，在开发适老化智能手环的过程中，科学评价是保证产品成功上市以及企业可持续正向发展的关键点；影响评价和决策的因素较多，需要参与决策的人根据若干个评价准则对多个设计方案进行评价与优选，其属于多准则群体决策的问题。

逼近理想解排序法(technique for order preference by similarity to ideal solution，TOPSIS)是一种行之有效的多准则决策方法，被广泛应用于管理与决策、环境管理、供应商选择、风险评估、商业市场管理研究、安全监管与仪器设备选择等领域[2]，而在产品设计方案的评价与优选中应用较少。但是TOPSIS法在权重计算部分没有完整的方法架构，而是完全根据决策者的主观认知确定准则权重[3]，因此有失客观性，可搭配其他方法使得该部分更加客观完整。本文在TOPSIS方法中引入基于三角模糊数的层次分析法(fuzzy analytic hierarchy process，FAHP)，对打分人员意见进行评定，采用定性与定量结合的方法，使各评价准则的权重值更加客观合理，可有效地解决评价时主观判断导致的误差或计算结果不准确等问题。

在决策过程中，AHP法提供各项评价准则的权重，TOPSIS法作为设计方案排序的主要工具，建立系统化和层次化的结构体系，对16款适老化智能手环的设计方案进行综合评价优选，最后得出最优的设计方案。

1 综合评价准则模型的建立

适老化智能手环设计方案的优选是一个涉及多层次、多准则等诸多因素的综合集合结果。在定夺一级与二级评价准则时，各因素之间互相制约、影响，因此必须要保证评价准则的选取具有全面性、无重叠性和代表性。

(1) 目标层。为适老化智能手环方案综合评价，该层的要素是唯一确定的。

(2) 准则层。对一款产品的评价应从多个方面展开，以此确保评价结果的全面性。结合专家访谈，从产品本身、用户、用户和产品之间还有生产者4个方面出发，将一级准则设为产品设计1、用户体验2、人机交互3和实际生产4，构建一级准则集合={1,2,3,4}。

(3) 子准则层。参照文献[4-5]用户与专家问卷的方法，初步针对4个一级准则层面拟定了21项准二级评价子准则1~5，6~10，11~14，15~21，见表1。由于有些评价准则不具有代表性且近似或重复，为避免评价准则被重复计算，因此结合老年人的特点，对初选评价准则进行了筛选，以确定最终的适老化智能手环评价准则体系，如下：

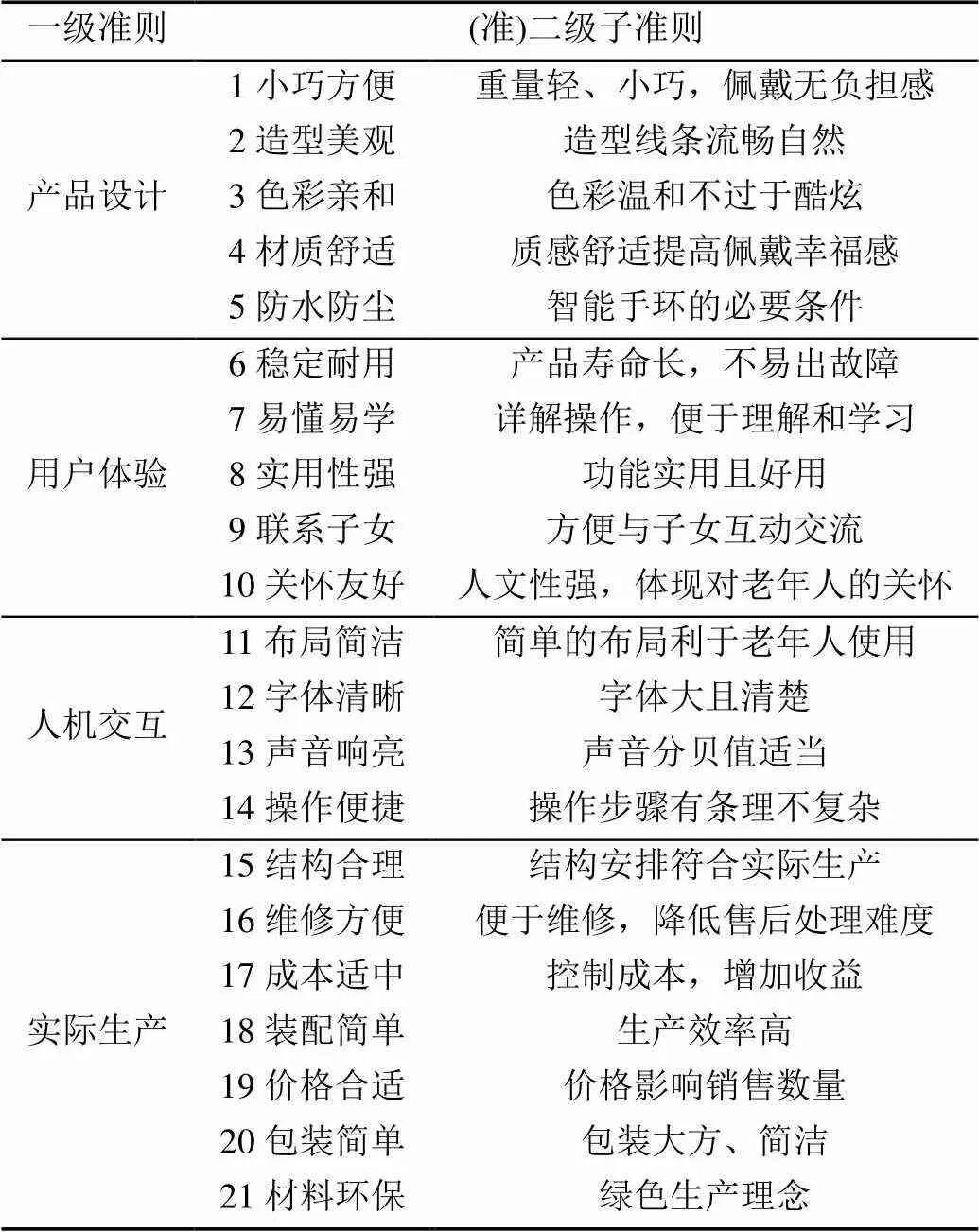
表1 一级评价准则与(准)二级评价准则

产品设计准则。从产品本身出发，提出小巧轻便1、色彩亲和2、材质舒适3和防水防尘44个二级子准则。

用户体验准则：从用户出发，结合老年人的喜好，通过问卷调查，对老年人的生理和心理特征进行深入剖析，挖掘老年人潜在的情感需求。综合调查结果来看，提出易懂易学5、实用性强6、关怀友好7和稳定耐用84个二级子准则。

人机交互准则。从使用者和产品之间的交互角度出发，提出布局简洁9、字体清晰10、声音响亮11和操作便捷124个二级子准则。

实际生产准则度。从生产者出发，一款好的产品，不只是停留在设计阶段，实际生产也会对其产生约束，提出结构合理13、成本适中14、包装便捷15和材料环保164个二级准则。

由此得到二级评价准则集合1={1,2,3,4}，2={5,6,7,8}，3={9,10,11,12}，4={13,14,15,16}。至此，基于模糊层次分析法构建出适老化智能手环的层级评价模型如图1所示。

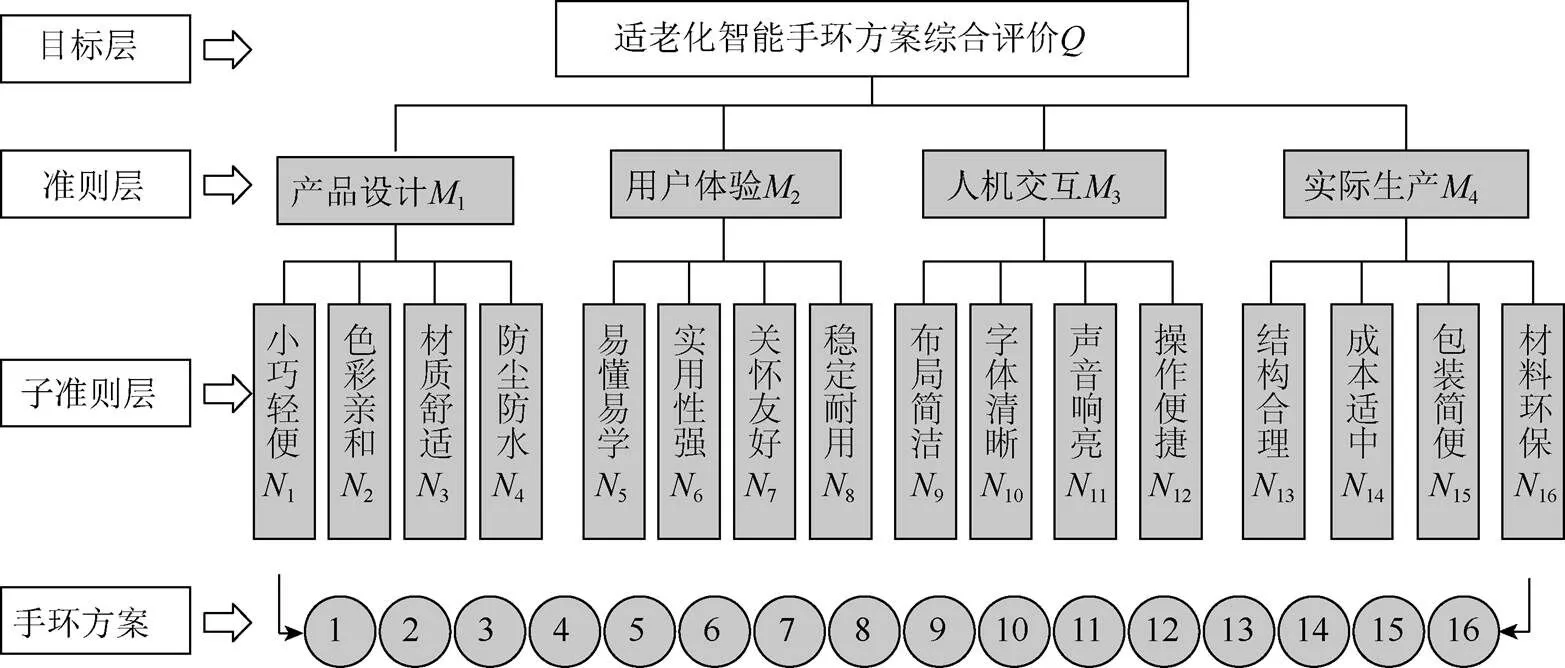
图1 适老化智能手环的层级评价模型

2 基于FAHP-TOPSIS法的适老化手环方案评价决策步骤

FAHP法是在层次分析法(analytic hierarchy process，AHP)的基础上，进一步丰富完善的结果[6]。在FAHP法中引入三角模糊数的概念从而模拟人在判断时思维的模糊特征，可以使各准则的最终权重排序存在一定的弹性调整空间；TOPSIS法是一种多准则决策方法，其基本思路框架是构造出决策问题的正理想解与负理想解，通过计算各个备选方案与理想解的接近程度来进行方案排序，从而完成最终的方案评价与优选，并且还可以从一定程度上辅助优化方案[7-8]。TOPSIS法能够充分利用每一个方案的定量数据信息，避免不同决策者因偏好不同对决策结果产生影响，从而提高决策科学性与可信度。

FAHP-TOPSIS方法结合了FAHP和TOPSIS2种方法的优点，提高了适老化智能手环方案决策的科学性和可信度。该方法主要包括2部分：

(1) 采用FAHP法对适老化智能手环各评价准则的权重进行计算。

(2) 采用TOPSIS法对适老化智能手环方案进行综合排序与评价优选。

2.1 基于FAHP法的准则权重计算

AHP法在定性分析的基础上进行定量分析，但是容易受到极值的影响，层次关系的建立易趋于主观性。FAHP法是基于模糊数学原理，用于研究具有模糊性的数学问题，将多要素与多属性结合，解决评估的模糊性和主观性[9]。评价步骤如图2所示。

图2 FAHP法主要计算步骤

2.1.1 构造准则层两两比较的模糊互反判断矩阵

FAHP法有基于模糊数和基于模糊一致性矩阵2种。本文采用三角模糊数辅助构造两两比较判断矩阵[10]。三角模糊数的确定通过采集3个数点来完成，可以克服在准则两两比较过程中因无法准确度量而只能用自然语言变量进行模糊评价的困难。其是针对目标层在一级评价准则之间进行比较与打分，构造出一级模糊互反判断矩阵；其次，针对一级准则，构造其二级子准则之间的模糊互反判断矩阵。依据两两比较法和比例标度法建立矩阵，由打分人员进行打分裁定。

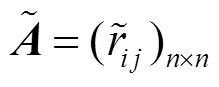
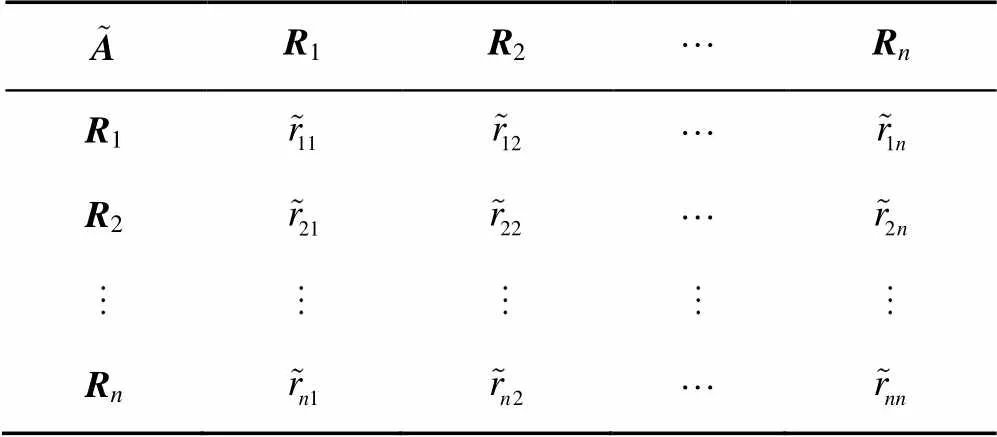
表2 模糊互反判断矩阵的构建

其中，和为进行对比判断的2项准则，上标表示该数据由第位打分人员给出。综合位打分人员的模糊判断矩阵，分别建立-层和-层模糊综合判断矩阵。假定各位同类别打分人员具有相近的知识量和判断水平，那么为每位打分人员取相同的权重，因此可以采用算术平均的方法综合评分信息。-层的模糊综合判断矩阵为

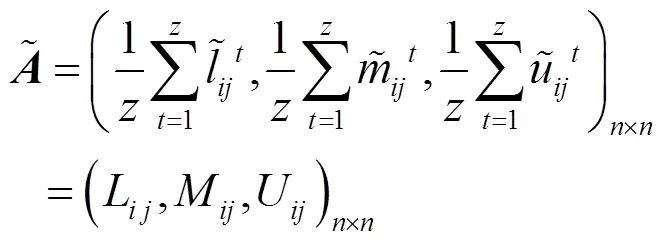
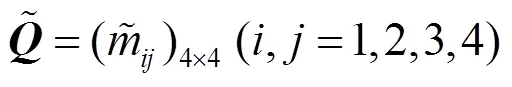
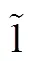
表3 -比例标度定义项的量化及含义

2.1.2 计算各矩阵权重值

(1) 模糊互反判断矩阵去模糊化计算。通常三角模糊数的去模糊化是先将其转化成精确数判断矩阵，继而按照经典AHP法进行一致性检验。根据文献[12]提出的方法，去模糊化式为

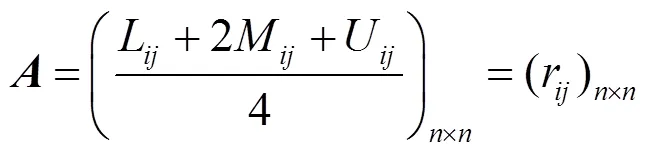
(2) 矩阵权重值计算。将所有的模糊互反判断矩阵去模糊化之后，开始计算每一个矩阵的权向量[13]。由于判断矩阵会存在一定偏差，因此计算精确度可以适当减小。采用近似算法──方根法，完成计算，具体步骤如下：

步骤1.计算判断矩阵的每行乘积

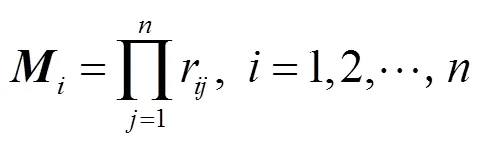
步骤2.计算的次方根w

步骤3.正规化处理向量求出权向量

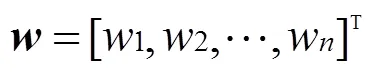
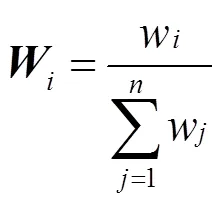
在这里，-层和-层模糊综合判断矩阵的权重值计算均采用以上计算过程。

2.1.3 特征向量计算及一致性检验

在实际决策的过程中，由于客观事物的复杂性及人类思维的局限性，专家所给出的判断可能存在前后不一致的问题，因此需要检验判断矩阵的一致性。若精确数判断矩阵具有一致性，那么也认为原三角模糊数判断矩阵近似具备一致性[14]。首先需要完成判断矩阵的最大特征值max的计算，然后开始检验一致性，该检验需要结合一致性准则、随机一致性准则和一致性比率来度量。在此，判断矩阵的平均随机一致性准则是依据经验取值，判断矩阵的最大特征值max，1~9阶判断矩阵的以及，的具体计算步骤如下：

(1) 计算判断矩阵的最大特征值，是特征矩阵

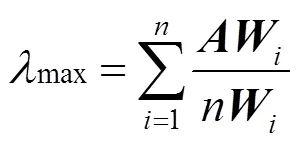
(2) 计算不一致程度，是判断矩阵的阶数

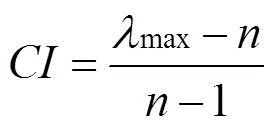
(3) 根据选取平均随机一致性准则，见表4。

表4 平均随机一致性准则

(4) 计算矩阵的随机一致性比率

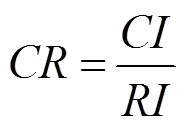
当<0.1时，判断矩阵具有良好的一致性，反之，则需要适当修改取值，直到达到良好的一致性，终止调整，完成层次单排序。

2.1.4 计算各综合排序的辅助排序

准则层各权重值的一致性检验完成后，需汇合各个层次的单排序，形成层次总排序，作为最终适老化智能手环方案评价的参照标准。本文有2个层次，即准则层和子准则层。例如：将子准则1的权重与其对应的准则1的权重相乘，即可得到子准则1的最终权重。同理计算出16个子准则的最终权重，并按大小进行排序，可以得到16个子准则的相对重要程度列表。

2.2 基于TOPSIS法的适老化智能手环方案综合评价

TOPSIS法是一种根据待评价方案与理想化方案的接近程度来进行排序的用于处理多准则问题的决策方法，可以对基础数据信息实现充分的利用，能准确、直观、可靠地反应各个方案之间的差距，具有较强的普适性[15]。本文在使用FAHP法求出各准则权重之后，采用TOPSIS法求出各方案与理想解的相对接近度，根据计算结果完成方案排序。综合评价决策步骤如图3所示。

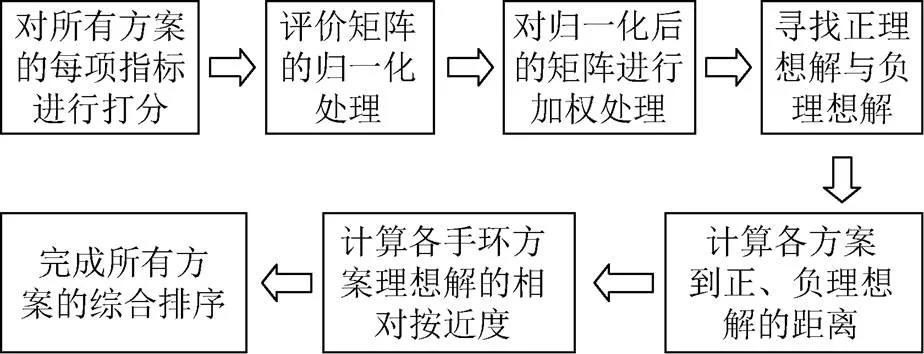
图3 TOPSIS法主要计算步骤

2.2.1 评价数据收集与矩阵处理

(1) 评价数据的收集。对各个方案的准则打分时，需要将定性判断采用定量数值的形式呈现，使所有数据的数量级接近，最终的结果更加精确[16]。定性语言意义与标度值之间的关系见表5。

表5 语义量化级别表

(注：2、4、6、8包含在其中)

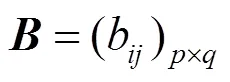
(2) 矩阵的归一与加权处理。因数据准则的离散化程度不同，所以需对矩阵进行归一化处理，保证所有数据分布在0~1之间，得到规范评价决策矩阵

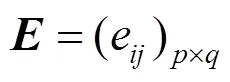
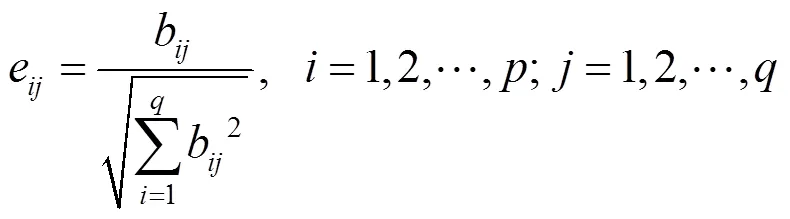
对规范评价决策矩阵进行加权处理，构成加权规范评价决策矩阵

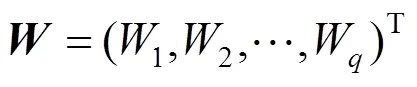
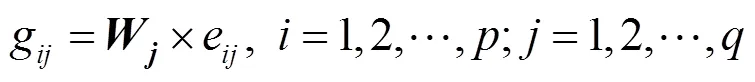
2.2.2 计算各方案与最优最劣解的接近程度并排序

(1) 寻找正、负理想解。在加权规范评价决策矩阵中，找出各子准则的最大值构成最优向量，即正理想解+，找出各子准则的最小值构成最劣向量，即负理想解–

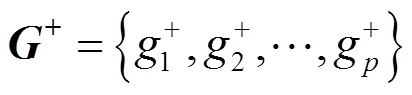
(2) 计算各适老化智能手环方案到正、负理想解的欧式距离。各适老化智能手环方案p到正理想解的距离为，到负理想解的距离为

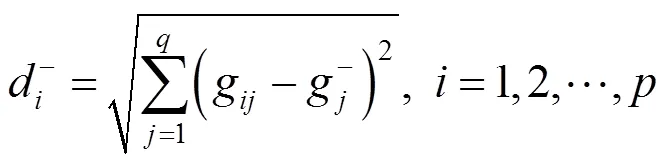
(3) 计算各适老化智能手环方案关于理想解的相对接近度H，并按照H对所有方案进行排序

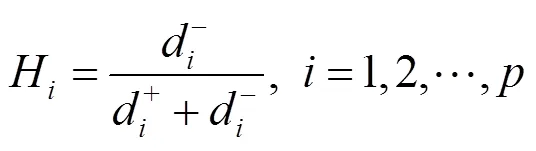
由式(16)可以看出HÎ(0,1]，H值越大，即越接近1，则表示手环方案与最优解越接近；反之，手环方案则与最劣解越接近。

(4) 方案综合排序。根据各适老化手环方案与正、负理想解的接近度，将所有方案进行排序，根据结果进行选择与决策。

3 适老化智能手环方案评价实例应用

我国现在已有较多老年人在使用智能设备，说明老年群体对智能产品的使用障碍存在消减趋势，对于高科技的产品接受度在逐步提高，老年群体将会成为智能穿戴产品市场庞大的潜在消费群体。本文选取了某品牌16个待评价设计方案，进行综合的评价与最终决策。

3.1 数据的收集

16款待评价方案，见表6。为了获得各评价准则的权重，-层由公司决策者群体进行统一评价打分，该层主要由产品开发者主观确定，与公司经营、设计理念等有关；考虑到-层的不同准则所需的打分人员类型不同，因此邀请了专家、设计师、老年人用户和生产者，总计35人，共同完成调查问卷，对定性准则进行模糊打分。35位打分人员的个人资料及其打分任务分配见表7。

表6 线稿方案展示

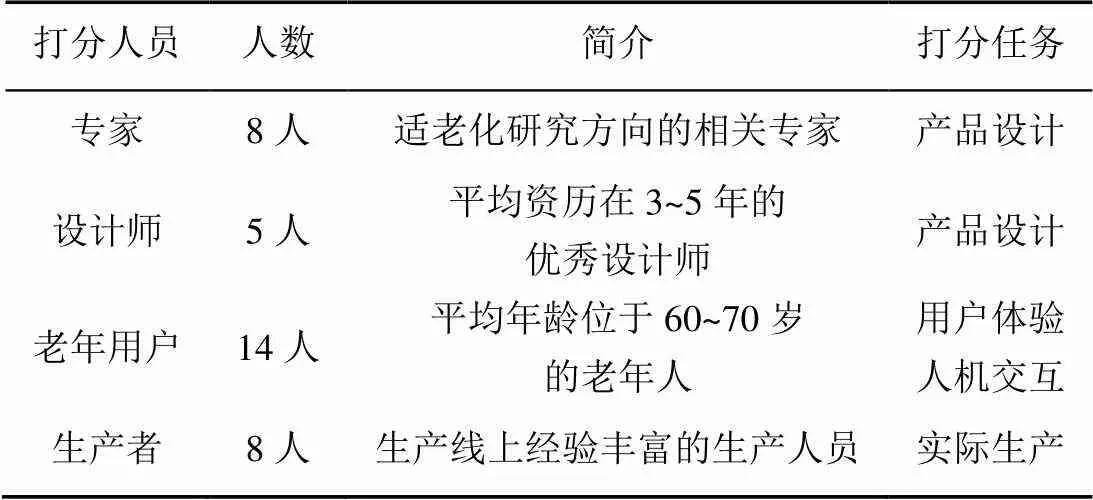
表7 打分人员资料汇总

3.2 计算结果

将问卷结果按照式(3)进行计算，得到各评价准则的模糊互反判断矩阵

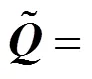
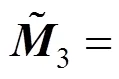
根据式(4)进行去模糊化处理，然后根据式(5)~(8)，求出各去模糊化矩阵的权向量，结果见表8~12。

表8 适老化智能手环方案综合评价判断矩阵及其权重

表9 产品设计准则判断矩阵及其权重

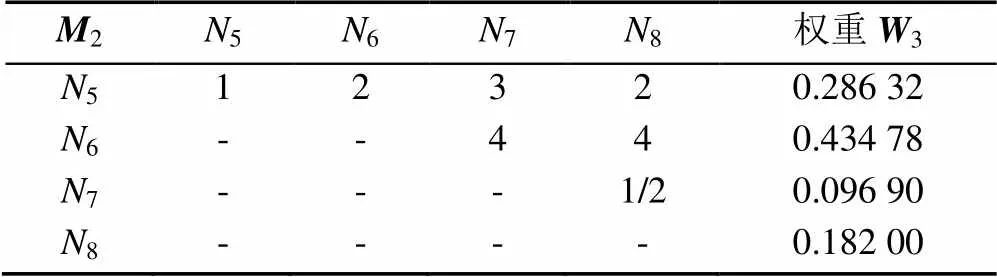
表10 用户体验准则判断矩阵及其权重

表11 人机交互准则判断矩阵及其权重

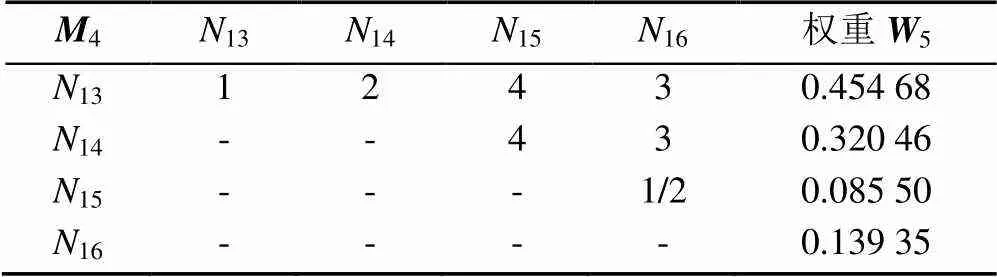
表12 实际生产准则判断矩阵及其权重

完成各矩阵的一致性检验，检验结果见表13。汇合所有矩阵的权重，形成层次总体排序，见表14及图4和图5。

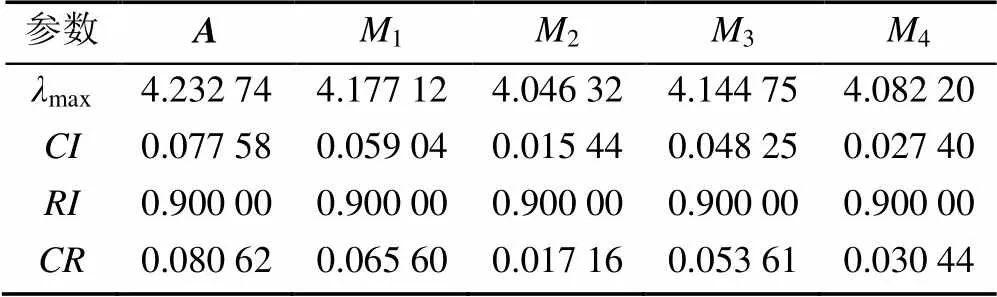
表13 一致性检验结果

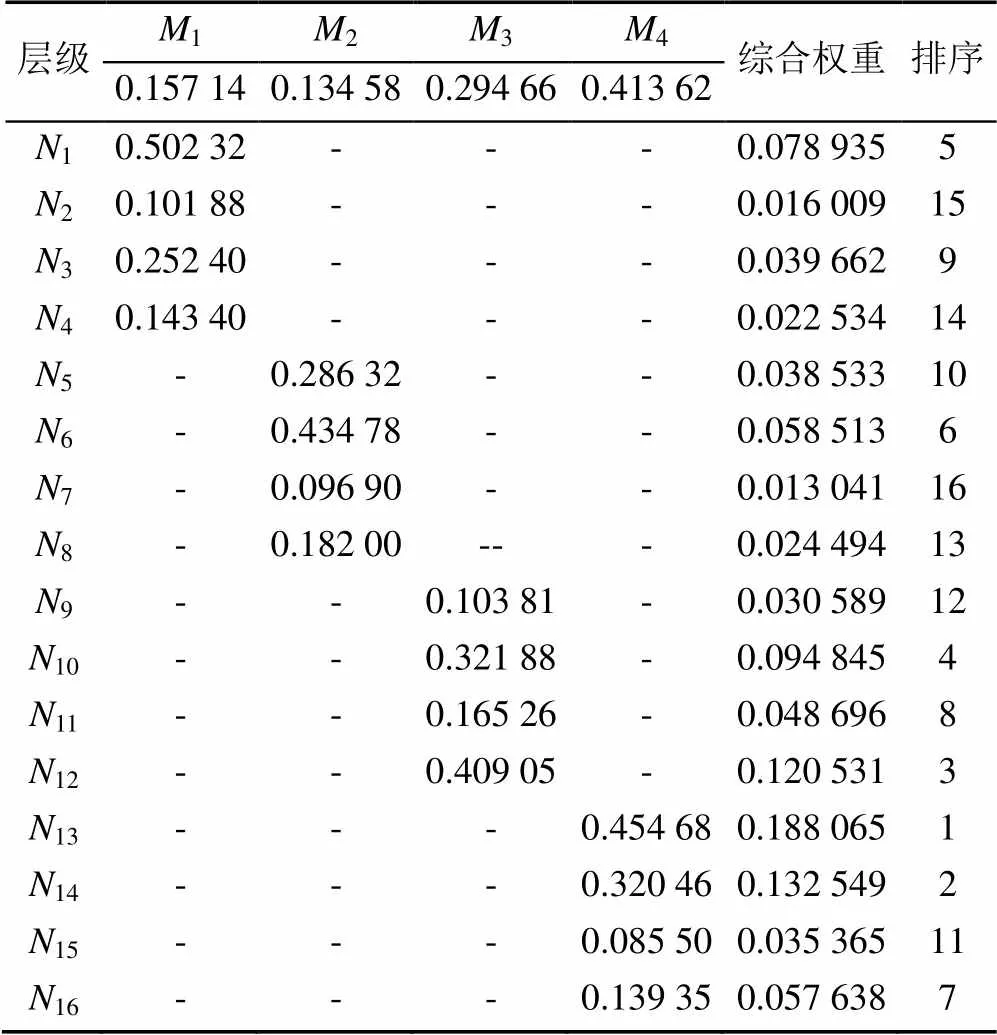
表14 所有子准则层次总排序

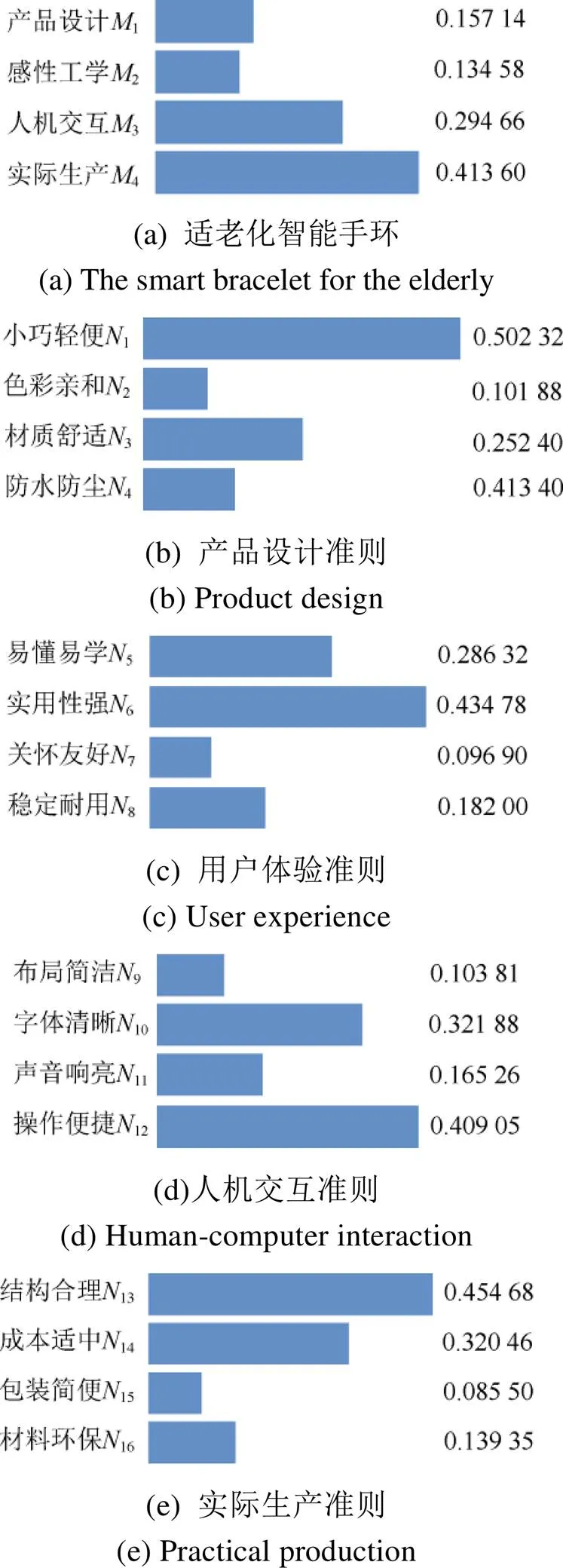
图4 子准则的权重单排序柱状图

图5 子准则的综合权重总排序柱状图

根据表5的语言变量信息，邀请与各准则对应的打分人员对表6中的16款设计方案的评价子准则进行打分，为了便于后续计算且和表5呼应，在得到平均数后，做了取整处理，构造出矩阵，如图6所示。根据式(12)，进行归一化处理，得到规范评价决策矩阵；根据式(13)，进行加权处理得到加权规范评价决策矩阵。为了便于运算，将得到的加权决策矩阵中的所有元素等比扩大100倍，并保留小数点后两位小数，结果如图7所示。从矩阵中找出正理想解+和负理想解–

根据式(14)~(16)计算出各适老化智能手环方案到正、负理想解的距离和-以及各手环方案关于理想解的相对接近度H，并根据H的大小对所有方案进行排序，结果见表15。

图6 专家、用户和生产者打分矩阵B

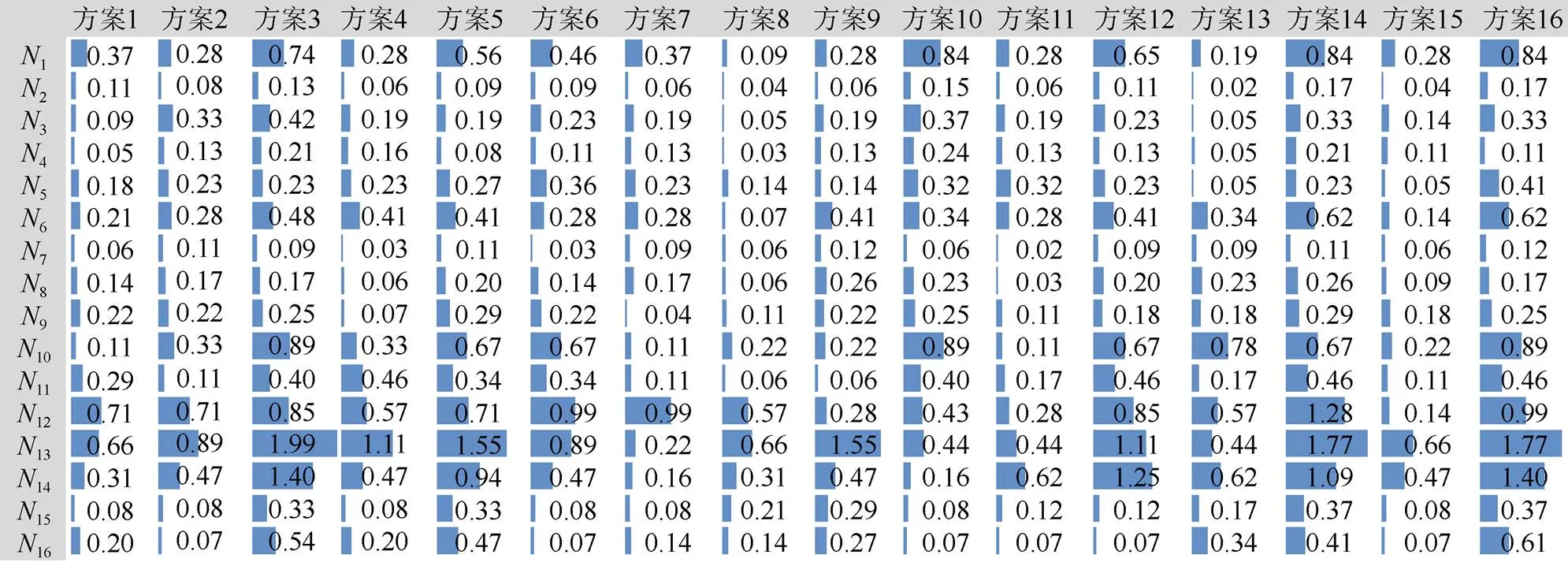
图7 加权规范评价决策矩阵G

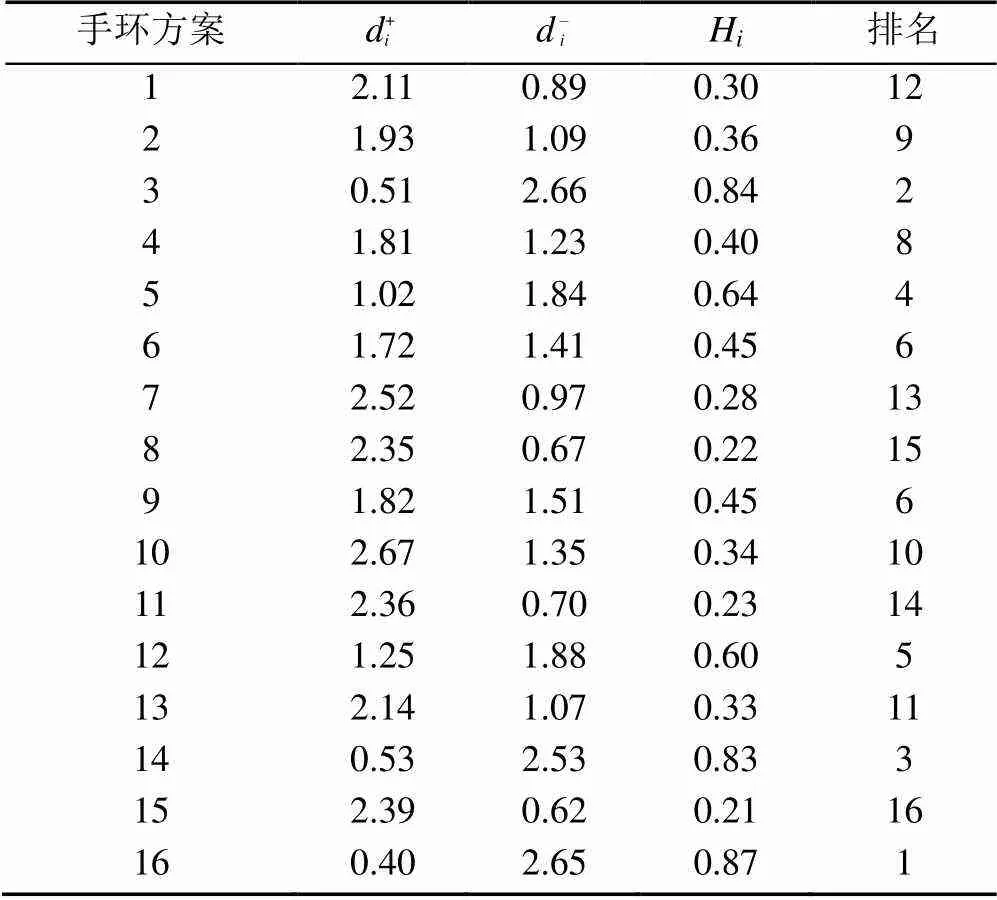
表15 16个适老化智能手环方案的排序结果

4 结果分析与方案优选

4.1 结果分析

根据FAHP-TOPSIS算法，得到了手环的16项子准则的权重，并结合对方案的打分，完成了16个待选设计方案较为合理的综合排序结果。

(1) 根据表14和图4，即层次单排序结果显示：在适老化智能手环评价的第一层准则内，实际生产准则在统计结果中占据最大权重，约为0.41，表明产品从设计到转化落地，实际生产最为关键，要结合生产实际绘制方案；人机交互准则权重占据第二，约为0.29，手环类产品没有流畅的交互操作，会影响用户体验；产品设计准则和用户体验准则所占权重接近，表明二者的重要程度相近。

在适老化智能手环评价的第二层子准则内，从属于产品设计准则层的小巧轻便子准则占据最大权重，约为0.50，在设计时要优先考虑。材质舒适子准则的权重次之，约为0.25。

从属于用户体验准则层的实用性强子准则在结果中占据最大权重，约为0.43，表明老年人在意产品实用性，设计产品时要注意老年人简朴节约的特质，满足其情感需求；权重占据第二的是易懂易学子准则，约为0.29，老年人对于智能产品的接受速度相对慢于年轻人，要注意提高产品的科技友好程度，易于学习理解。

从属于人机交互准则层的操作便捷子准则在结果中占据最大权重，约为0.41，说明操作方法简便，容易被老年人接受；权重值排在其后的是字体清晰子准则和声音响亮子准则，设计时要考虑老年人的视力和听力下降的因素，字体和声音的设计应有别于普通手环。

从属于实际生产准则层的结构合理子准则在统计结果中占据最大权重，约为0.45，结构不合理，会直接影响实际生产，设计方案不能侧重于外形设计而忽略内部构造；成本适中子准则也占据较大权重，说明成本的重要性，产品的最终目的是销售盈利。

(2) 根据表14和图5，即层次总排序结果显示：适老化智能手环从设计到落地生产整个过程中，结构合理子准则在统计结果中占据最大权重，成本适中子准则次之，这2项子准则均从属于实际生产准则，证明了实际生产环节的重要性。操作便捷、字体清晰、小巧轻便等子准则均占据较大权重，从侧面反映出老年人手环应具备较强的针对性。实用性强、材料环保、声音响亮、材质舒适和易学易懂等子准则的权重之间差距不明显，设计时应注意将差距不明显的子准则一同纳入考虑范围，不能遗漏。

综合所有子准则的排序可以看出，该排序结果具有很强的适老化特征，可依据其进行方案评价与优化，有利于扎实手环产品适老化的定位，辅助打造专门针对于老年人的智能手环。

(3) 以上皆为评价准则排序的分析，根据表15最终的方案排序结果，做出如下评价：

方案16>方案3>方案14，位列前3，与理想解的接近程度分别为0.87、0.84、0.83。方案12>方案5，位列第4和第5，与理想解的接近程度为0.64、0.60。

另外，从图6可以看出，方案10关于产品设计、用户体验和人机交互准则的评分，与排名前3的方案14与16相差不大，但在实际生产准则的评分明显落后，说明设计方案若不能与生产环节对接，在选择阶段会直接被淘汰。综合排名占据第2位的方案3，在产品设计、用户体验和人机交互准则中的评分均不及排在第1位的方案16，且和个别名次靠后的方案在上述准则中的评分差距不大，但由于其在实际生产准则内评分突出，所以最终排名靠前。可见，当产品方案的评价涉及到落地生产时，结构、成本、材料和包装等问题都是影响结果的关键因素。企业最终选择的方案，往往不是外观最突出的方案，而是兼顾外观、情感和交互的基础上，选择最贴合实际生产要求的方案。

4.2 方案优选

若最终只选择一个最佳方案，则方案16为最佳选择；若最终可选择多个方案，则推荐排在前3位的方案16、方案3和方案14，因为其与理想解的接近程度均在0.80以上，明显优于其他方案，决策者可根据实际需要，继续进行相应的优化筛选。方案5和方案12与理想解的接近程度均在0.60以上，也可酌情考虑并稍作调整与修改，有望提高排名。其他剩余方案，与理想解的接近程度均在0.50以下，评分低，不考虑。结合图7中的评价结果，提出的方案优选与优化思路见表16，以下思路缺少实际算法的客观指导，具有较强的主观性。

4.3 方案展望

本文使用FAHP法与TOPSIS法相结合的综合算法，可有效筛选出最佳方案，该最佳方案不仅综合评分最高，而且其大部分子准则的评分均优于其他方案，产品定位精准，对老年人具有较强的适用性，比较适合投入生产。但是企业不是必须选择排名第1的方案，排名前2~5的方案与理想解均在接近的程度范围内，参考表16的优化思路，可有针对性地将方案进行相应的改良与调整，从而有效提高其落地可能性，均可被列入投放生产的考虑范围内。该FAHP-TOSIS评价优选算法不仅可以将若干设计方案进行综合排序，从而选出最佳方案，也可以根据其运算过程中的数据统计结果，发现设计方案的不足之处，提供有效优化建议，从而提高设计效率。但是，设计师或决策者只能根据评价数据进行主观分析，从而对产品方案做出优化改良，这是其不足之处，之后可结合人工免疫等智能算法做进一步的完善与研究。

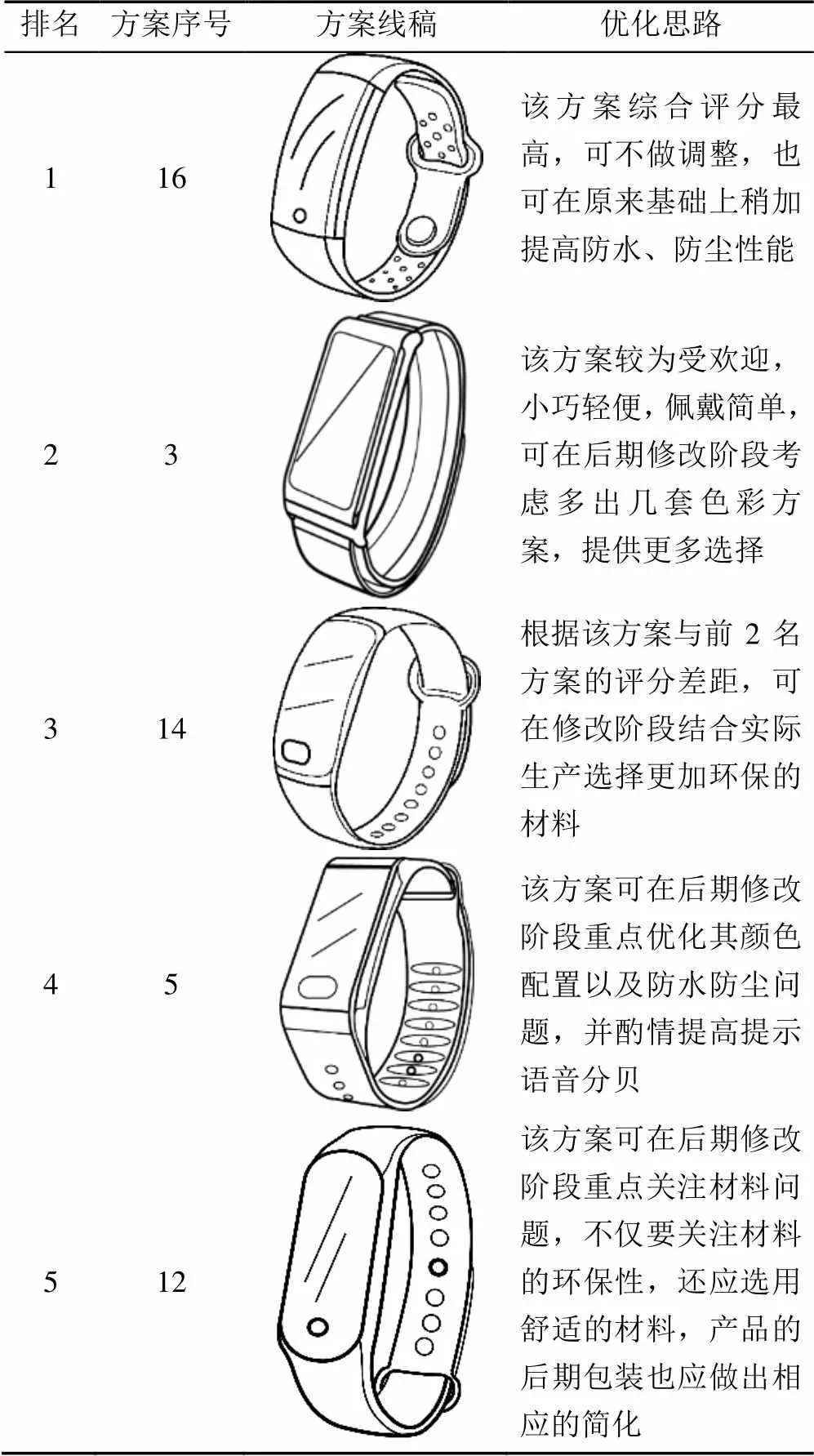
表16 方案优选与优化思路

5 结束语

在我国逐渐步入老龄化社会的发展背景下，针对适老化智能手环产品，选出4个一级准则，并在每个一级准则下筛选出4个二级子准则，构建出适老化智能手环方案的评价模型。将FAHP和TOPSIS方法相结合，能有效处理专家评价时的模糊性，并更加准确的计算出每个评价准则的权重和各个方案的综合排序情况。这将会在适老化智能手环，甚至更多其他类的适老化产品研发中，发挥至关重要的作用。本文以某品牌公司的10款备选适老化智能手环渲染方案为对象，分析了这些方案的优缺点并作出最终的优选决策。采用FAHP-TOPSIS法，可以帮助制定更合理的产品研发计划，更好完成适老化智能手环的方案制定。本文的研究思路和方法对适老化产品的研究具有一定的借鉴意义，对其他产品开发的方案评价与优选过程中也具有一定的适用性。如果在TOPSIS法的打分部分，可以更多的考虑到人的思维模糊性，会使该方法得到更进一步的完善。

[1] 石园, 吴海平, 张智勇, 等. 人因工程下不同养老模式的适老化设计研究[J]. 中国老年学杂志, 2016, 36(4): 987-991. SHI Y, WU H P, ZHANG Z Y, et al. Research on aging design of different pension models under human factors project[J]. Chinese Journal of Gerontology, 2016, 36(4): 987-991 (in Chinese).

[2] 徐玖平, 吴巍. 多属性决策的理论与方法[M]. 北京: 清华大学出版社, 2006: 55-60. XU J P, WU W. The theory and method of Multi-attribute decision-making[M]. Beijing: Tsinghua University Press, 2006: 55-60 (in Chinese).

[3] YANG W, CHEN Z P, ZHANG F. New group decision making method in intuitionistic fuzzy setting based on topsis[J]. Technological and Economic Development of Economy, 2015, 23(3): 441-461.

[4] 周明, 李亚军. 面向中国特色养老服务的产品交互适老化设计研究[J]. 艺术百家, 2017, 33(1): 233-234. ZHOU M, LI Y J. Interactive service design for the aged in china[J]. Hundred Schools in Arts, 2017, 33(1): 233-234 (in Chinese).

[5] 刘宗明, 葛碧慧. 基于QFD的老年家用陪护机器人设计[J]. 图学学报, 2018, 39(4): 695-699. LIU Z M, GE B H. Design of elderly household companion robot based on QFD[J]. Journal of Graphics, 2018, 39(4): 695-699 (in Chinese).

[6] 吴爱强, 汪永超, 李波, 等. 面向绿色制造的机械结构设计方案选择[J]. 组合机床与自动化加工技术, 2019, (10): 15-19. WU A Q, WANG Y C, LI B, et al. The scheme selection of mechanical structure design for green manufacturing[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2019(10): 15-19 (in Chinese).

[7] LI X R, YU S H, CHU J J. Optimal selection of manufacturing services in cloud manufacturing: a novel hybrid MCDM approach based on rough ANP and rough TOPSIS[J]. Journal of Intelligent & Fuzzy Systems, 2018, 34(6): 4041-4056.

[8] 葛畅, 余隋怀, 陈登凯, 等. 基于满意度与投入约束的产品技术特征配置[J]. 计算机集成制造系统, 2012, 18(2): 225-229. GE C, YU S H, CHEN D K, et al. Configuration of product technical characteristics based on satisfaction and input-constraint[J]. Computer Integrated Manufacturing Systems, 2012, 18(2): 225-229 (in Chinese).

[9] 李雪瑞, 余隋怀, 初建杰. 云制造模式下采用Rough-ANP的机械设计知识优选推送策略[J]. 机械科学与技术, 2018, 37(9): 1387-1395. LI X R, YU S H, CHU J J. Optimal selection strategy of mechanical design knowledge via Rough-ANP in cloud manufacturing environment[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(9): 1387-1395 (in Chinese).

[10] 李永锋, 朱丽萍. 基于模糊层次分析法的产品配色设计[J]. 机械科学与技术, 2012, 31(12): 2028-2033. LI Y F, ZHU L P. Product color design based on fuzzy analytic hierarchy process[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(12): 2028-2033 (in Chinese).

[11] 张先庚, 林琴, 张夏梦, 等. 基于德尔菲法构建老年健康状况评价表[J]. 中国老年学杂志, 2019, 39(22): 5623-5627. ZHANG X G, LIN Q, ZHANG X M, et al. Construction of elderly health evaluation table based on Delphi method[J]. Chinese Journal of Gerontology, 2019, 39(22): 5623-5627 (in Chinese).

[12] 李士勇. 工程模糊数学及应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004: 102. LI S Y. Engineering fuzzy mathematics and its application[M]. Harbin: Harbin Institute of Technology Press, 2004: 102 (in Chinese).

[13] 邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7): 93-100. DENG X, LI J M, ZENG H J, et al. Weight calculating method and its application of analytical hierarchy process[J]. Mathematics in Practice and Theory, 2012, 42(7): 93-100 (in Chinese).

[14] 陈明, 郭立新. 基于AHP-熵权-TOPSIS的电动汽车动力性经济性综合评价方法[J]. 机械设计, 2013, 30(4): 15-19. CHEN M, GUO L X. Comprehensive evaluation method of power economy of electric vehicle based on AHP-entropy weight-TOPSIS[J]. Journal of Machine Design, 2013, 30(4): 15-19 (in Chinese).

[15] 陈香, 邱大鹏. 基于模糊Kano模型与TOPSIS法的产品设计研究[J]. 图学学报, 2019, 40(2): 315-320. CHEN X, QIU D P. Research of product design based on Fuzzy-Kano model and TOPSIS[J]. Journal of Graphics, 2019, 40(2): 315-320 (in Chinese).

[16] 彭道刚, 卫涛, 赵慧荣, 等. 基于D-AHP和TOPSIS的火电厂控制系统信息安全风险评估[J]. 控制与决策, 2019, 34(11): 2445-2451. PENG D G, WEI T, ZHAO H R, et al. Control and decision, cyber security risk assessment of power plant control system based on D-AHP and TOPSIS[J]. Control and Decision, 2019, 34(11): 2445-2451 (in Chinese).

Comprehensive evaluation and optimization method of products for the elderly based on FAHP and TOPSIS——a case study on the smart bracelet for the elderly

YANG Mei, CONG Yang-fan, LI Xue-rui

(College of Design and Arts, Shandong University of Science and Technology, Qingdao Shandong 266590, China)

In order to comprehensively evaluate the smart bracelet for the elderly more thoroughly, an evaluation model was established, so as to facilitate the evaluation and optimization of the final scheme. The model was established from such 4 dimensions as product design, user experience, human-computer interaction and practical production. Firstly, the fuzzy analytic hierarchy process (FAHP) method was employed based on the triangular fuzzy number to acquire weight values of every index. Then, the technique for order preference by similarity to ideal solution (TOPSIS) method was utilized to evaluate and order every scheme. An example could be found in 16 schemes of the smart bracelet for the elderly of a certain brand and prove the feasibility and practical significance of this FAHP-TOPSIS method. Such an evaluation and optimization method can help solve problems in consideration of the fuzzy thinking to systematize, hierarchize and quantify the thinking process. It can thus ultimately propose a clear evaluation scheme and optimized method for the smart bracelet for the elderly.

suitable for the elderly; smart bracelet; fuzzy analytic hierarchy process and technique for order preference by similarity to ideal solution; comprehensive evaluation; scheme optimization

TP 391

10.11996/JG.j.2095-302X.2020030469

A

2095-302X(2020)03-0469-11

2019-12-01；

2020-03-06

山东科技大学优秀教学团队建设计划项目(JXTD20170509)；山东省2018年研究生导师指导能力提升项目(SDYY18082)；山东省文化创意与设计服务云平台构建策略研究项目(QN201906118)

杨 梅(1973-)，女，山东泰安人，教授，博士，硕士生导师。主要研究方向为工业设计及其理论。E-mail：skdyangmei@163.com

丛扬帆(1995-)，女，山东蓬莱人，硕士研究生。主要研究方向为工业设计及其理论。E-mail：yangfan_cong@sina.com