不同时间尺度下冻融灌区地下水埋深CAR模型优选

李仙岳 崔佳琪 史海滨 孙亚楠 邢进平

(1.内蒙古农业大学水利与土木建筑工程学院， 呼和浩特 010018；2.河套灌区永济灌域管理局， 巴彦淖尔 015000)

0 引言

地下水作为人类赖以生存的水资源，特别是在我国西北干旱地区，在维持区域社会经济和生态可持续发展方面起到重要作用[1-2]。由于气候变化、不合理的农业灌溉、排水不畅等因素，导致部分区域地下水位超过临界水位，土壤盐碱化问题突显[3]，影响了灌区生态环境的健康发展和农业的可持续发展。另外，一些区域由于大规模节水改造工程的实施，导致地下水位下降，从而使作物利用地下水量下降、灌溉水量增加[4]。准确预测灌区地下水埋深对于农田灌溉研究以及灌区合理用水都具有重要意义[5]。由于地下水埋深受自然条件和人类活动双重作用的影响，其变化过程非常复杂[6]。

目前，对地下水位预测的研究方法较多，主要包括基于物理模型的数值模拟和基于数据驱动的机器学习算法[7]。其中，数值模拟主要是基于MODFLOW、FEFLOW等模型进行的各种地下水动态模拟。如杨洋等[8]应用MODFLOW模型对井渠结合后内蒙古河套灌区地下水动态变化进行模拟，并进行了验证；杨广等[9]基于MODFLOW模型对玛纳斯河流域下游地下水位进行了预测，发现通过调整种植结构可减少地下水开采量，以减少地下水负均衡量；LI等[10]应用FEFLOW模型对黑河流域绿洲水文过程进行模拟，结果表明，在现状和节水措施下，未来10年的地下水位将持续下降。数值模拟方法对边界条件、水文地质参数等要求严格，参数较难获取，而且由于边界及含水层的设置不当容易导致预测精度降低、模拟失真等[11-12]。

地下水预测的机器学习算法主要基于BP神经网络[13-14]、灰色系统模型[15]、支持向量机[16]、马尔科夫链[17-18]等模型，这些模型各具特点，且不需要各类物理参数，因此在不同学科中均得到了广泛应用。但这些预测模型的建模方法要求时间序列具有平稳性、独立性和正态性，如果时间序列过于复杂，则得到的预测结果不精确。多变量时间序列CAR(Controlled auto-regressive)模型结合了回归分析和一维时间序列分析两种方法的优点，能够较好地模拟和预报，避免了因处理复杂时间序列而引起的误差。目前已广泛用于水文领域的径流、水量及人口增长、气候变化趋势等预测上[19-24]。管孝艳等[25]基于时间序列CAR模型对河套灌区沙壕渠灌域地下水埋深进行了预测，预测效果良好，证明该模型具有较好的适用性。ZENG等[26]基于多变量时间序列建立了洞庭湖地区地下水资源预测模型，并对不同方案下的地下水资源量进行了预测。YAO等[27]基于CAR模型预测了气候变化及人类活动对艾比湖流域3条河流年径流量的影响，其中博尔塔拉河和径河的年径流量呈增加趋势，而奎屯河呈轻微减少趋势。另外，基于多变量时间序列模型和其他模型的耦合使用也得到了广泛应用。如张展羽等[28]基于主成分分析与多变量时间序列进行耦合，对济南市陡沟灌区的地下水位进行预测，结果表明，适当引入地表水灌溉和减少地下水开采，灌区地下水位将逐步回升；MANZIONE等[29]基于时间序列结合地质统计学构建了随机模型，用于巴西东南部Guarani含水层出露地区的地下水位预测，为地下水管理提供了重要决策依据。

多变量时间序列模型在地下水预测中得到了广泛应用，但北方灌区冬季气温低，存在冻融期，如河套灌区有超过5个月的冻融期，冻融期内地下水埋深受到气温的约束[30]，所以采用年尺度数据源构建CAR模型势必会忽略冻融造成的误差，而采用月尺度数据源构建CAR模型又难以刻画引水等因素的滞后效应，同时在冻融地区CAR模型中是否增加气温这个输入变量也会对预测结果产生影响。目前针对冻融区基于不同时间尺度数据源CAR模型的地下水预测研究较少。本文以河套灌区永济灌域为研究对象，研究不同时间尺度(月、季、年)数据源，并考虑不同影响因子输入变量，应用多变量时间序列CAR模型进行地下水动态变化预测，并对其差异性进行分析，优选适合冻融灌区的CAR地下水预测模型，以期为该冻融灌区地下水的准确预测提供理论依据。

1 材料与方法

1.1 研究区概况

永济灌域(107°13′～107°42′E，40°36′～41°13′N)地处河套灌区中部，蒸发强烈、干燥少雨、日温差大、日照时间长，年平均降水量133 mm，年平均蒸发量2 327 mm，蒸发量是降水量的10～16倍，年平均气温7.5～9.7℃，属于典型的温带大陆性干旱、半干旱气候。农业用水几乎全部引于黄河水，1999—2017年引黄水量在7.4～10.5亿m3之间。灌域地形西南高，东北低，地下水总的流向自西向东，大部分的浅层地下水靠灌域内数条自南而北的排水干渠汇入北部由西向东的总排水干渠，然后再经总排水干渠流入东部的乌梁素海，地下水的运动以垂直交替为主。地下水的主要补给来自引黄的入渗补给，其次为降水入渗补给。蒸发消耗为灌域主要排泄途径，地下水循环属于典型的入渗-蒸发类型。11月下旬至翌年4月为灌域的冻融期，冻结至融通历时180 d。按水文地质特点灌域内水文地质结构分为第一含水层组和第二含水层组。第二含水层组埋深较大，与外界水量交换较少，且以咸水为主，不宜开采利用，故本文以第一含水层组为研究对象。

1.2 数据采集和处理

在永济灌域内共布设了44眼长期地下水观测井(图1)，采用人工法在每月1、5、11、21、26日测地下水位埋深，并在干渠设流量日监测点，数据来源于永济灌域管理局，监测时间为1999—2017年。气象数据来源中国气象科学数据共享网(http:∥data.cma.cn/)，包括1999—2017年逐月平均气温、逐月累计降雨量、逐月累计水面蒸发量。

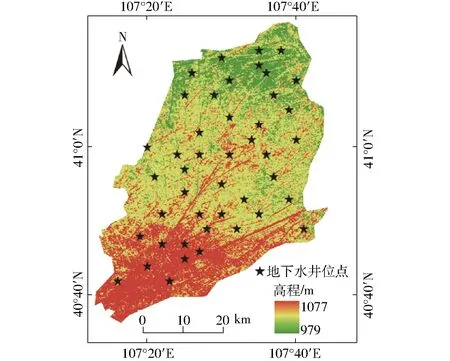
图1 永济灌域地下水采样点分布Fig.1 Distribution of groundwater sampling points in Yongji irrigation field

2 基于多变量时间序列CAR的地下水预测模型

2.1 CAR模型建模原理

多变量时间序列CAR模型主要采用递推最小二乘法进行模型参数评估的方法建模[31-32]。由m个输入变量和1个输出变量组建成n阶CAR模型，其形式为

yt=a1yt-1+a2yt-2+…+anyt-n+b10x1,t+b11x1,t-1+…+b1nx1,t-n+b20x2,t+b21x2,t-1+…+b2nx2,t-n+…+bm0xm,t+bm1xm,t-1+…+bmnxm,t-n+εt

(1)

式中 {an}、{bmn}——系数，其中m为正整数，n为非负整数

t——时间序列编号，t>n

yt——输出变量

xm,t-n——输入变量

εt——残差

2.2 CAR模型建模步骤

(1)CAR模型的参数估计

采用递推最小二乘法参数估计

θ=[a1,a2,…,an;b10,b11,…,b1n;b20,b21,…,b2n]Tzt=[yt-1,yt-2,…,yt-n;x1,t-0,x1,t-1,…,x1,t-n;x2,t-0,x2,t-1,…,x2,t-n]T

则CAR模型的一般形式可以写为

(2)

根据式(2)，在时刻t，θ的递推最小二乘估计值为

(3)

式中β——遗忘因子，一般取0.9～1.0

I——单位矩阵

参数Pt初值为λI，其中λ取104，则可利用N组观察值得到的CAR(n)模型计算残差平方和

(4)

(2)CAR模型最高阶n的判定

根据已知的N样本(xj,t,yt)(t=1,2,…,N;j=1,2,…,m)，由低阶到高阶递增地对系统进行拟合，并且依次对相邻的两个CAR模型采用F检验的方法判断模型阶次增加是否合适，得出合适的CAR模型。

(5)

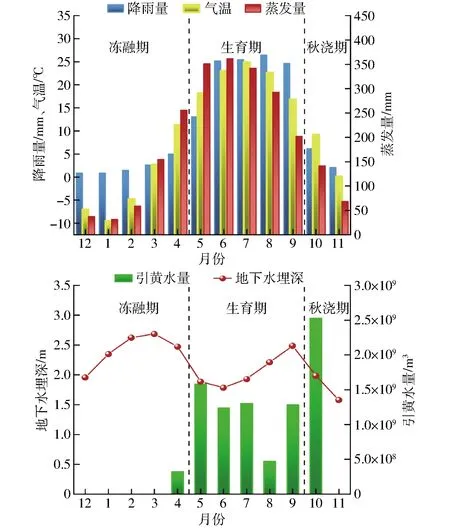
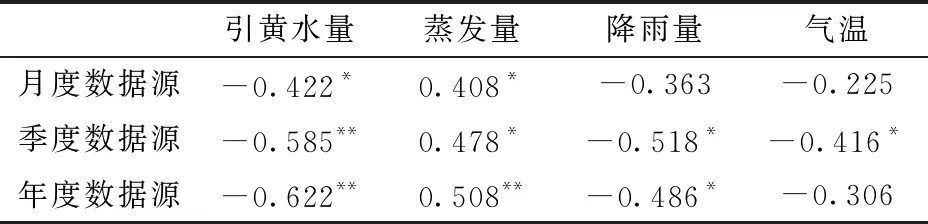
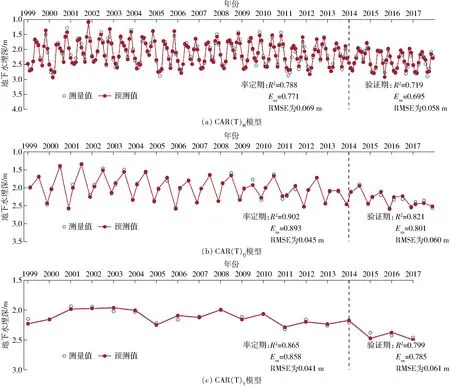
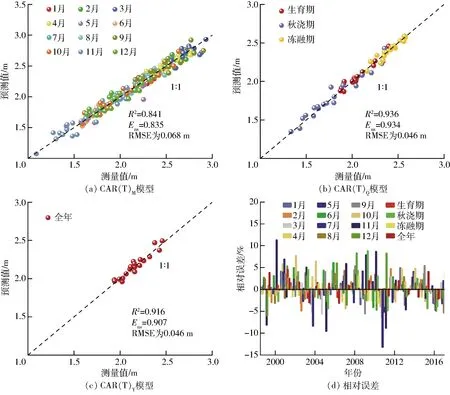
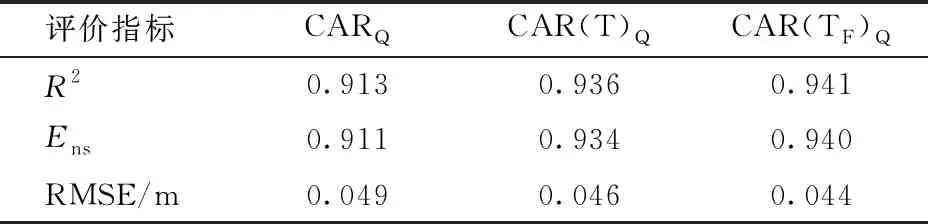
取置信度α=0.05，大均方自由度为m，小均方自由度为N-mn-(m+1)，求出相应的临界值Fα。若F

(3)CAR模型真实阶及时滞的检验

为避免以上步骤后某些参数可能为0，对CAR(n)模型中某些系数是否为0进行F检验，将接近于0的参数剔除后，重新应用递推最小二乘法建立较少参数的CAR(n)模型，并继续采用F检验的方法进行检验。若不显著，则较少参数的CAR(n)模型是真实模型；若显著，则原来的CAR(n)模型是真实模型。用以决定模型的真实阶及其时滞，得到真实模型的参数估计。

经过上述3个步骤，即可建立只保留对系统影响较大因素的较少参数CAR(n)模型。

(4)模型的率定和验证

由于永济灌域有超过5个月的冻融期，考虑到不同时期气温因素对地下水埋深的影响不同，本文以永济灌域1999—2017年月均、季均(生育期-秋浇期-冻融期)、年均引水量X1(亿m3)和蒸发量X2(mm)、降雨量X3(mm)、气温X4(℃)作为输入变量，地下水埋深Y(mm)作为输出变量，建立不同时间尺度数据源(月、季、年)不考虑气温、考虑气温和只考虑冻融期(12月到翌年4月)气温的地下水埋深预测模型。建模及因子检验的显著性水平为0.05，建模所用递推最小二乘法的遗忘因子为1.0。为验证模型的可行性，以不同时间尺度考虑气温因素的CAR(T)模型为例，月尺度数据源、季尺度数据源和年尺度数据源CAR模型分别记为CAR(T)M、CAR(T)Q和CAR(T)Y，其中1999—2013年数据用于模型的率定，2014—2017年数据用于模型的验证。

2.3 模型评价指标

采用决定系数(R2)、均方根误差(RMSE)和Nash-Sutcliffe系数(Ens)3种指标[33-34]对各模型模拟效果进行评价。其中R2和Ens越接近1，RMSE越小，说明预测值与实测值相差越小，拟合精度越高。反之，模型拟合精度较差。同时，通过对实测值与预测值的拟合误差进行分析，进一步评价模型的模拟精度。

3 结果与分析

3.1 地下水埋深影响因素分析

随着灌区续建配套及节水改造的大规模实施，总体上灌域地下水埋深呈下降趋势，1999—2017年期间，永济灌域年平均地下水埋深为2.16 m。按照灌域的灌水特征，通常在每年4月中旬开闸引水，11月中旬停灌，其中大规模秋浇时间为10月和11月，而在12月至翌年4月河套灌区土壤和地下水处于封冻-消融阶段。为了便于季尺度地下水预测，将全年分为3个阶段，其中12月—翌年4月为冻融期，5—9月为生育期，10—11月为秋浇期。由图2可知，年内地下水埋深的变动主要受引水及生育期耗水的影响呈季节性周期变化，土壤于11月中旬开始冻结，冻层厚1～1.5 m，随着冻层的逐渐加厚，地下水埋深随之下降，土壤蒸发降至最小，至翌年3月出现全年最大埋深。此期埋深的下降是由于冻层上下温差较大，地下水在温差作用下，向冻层运移，使冻层不断增厚，使地下水埋深加大。翌年3月无降水与灌溉入渗补给，在冻结影响下为全年最大埋深2.68 m，土壤消融始于3月初，于4月末完全解冻，冻层以下融冻水回补地下水，埋深开始上升。冻融期年均地下水埋深为2.42 m，其主要影响因素是土壤温度，而土壤温度受外界气温影响[35-36]。5月中旬夏灌开始，地下水位大幅度上升，同时蒸发作用剧烈，地下水消耗于蒸发，埋深出现峰谷交替变化，生育期间年均地下水埋深波谷出现在6月，为1.78 m，波峰出现在9月，为2.49 m，月均埋深为2.06 m。10月开始大规模秋浇，灌水量大，时间短，这一阶段地下水埋深变浅，由于存在一定的滞后性，至11月出现全年最小埋深1.57 m。非冻融期(生育期和秋浇期)，入渗与蒸发之间的平衡关系是地下水埋深变化的主导因素[37]。

图2 永济灌域地下水埋深及其影响因素Fig.2 Groundwater depth and its influencing factors in Yongji irrigation field

通过对近20年(1999—2017年)灌域地下水埋深与引黄水量、蒸发量、降雨量以及气温进行相关分析(表1)，结果显示这几项环境因子与地下水埋深均有较好的相关性，其中引黄水量和蒸发量均达到极显著相关，可见该区域水分入渗和耗水是其地下水变动的主导因子，而且降雨量和气温也与地下水埋深呈显著相关。另外总体上不同尺度(月、季、年)地下水埋深与环境因子的相关性比较相近，不同时间尺度数据源相关性由大到小总体上依次为：年度、季度、月度，这可能是由于年尺度通过数据平均弱化了变异点的影响。

表1 地下水埋深相关因子分析Tab.1 Analysis of correlation factors of groundwater depth

3.2 不同时间尺度数据源地下水CAR模型的构建与验证

图3 不同时间尺度地下水CAR(T)模型率定及验证Fig.3 Calibration and verification of groundwater CAR(T) model at different time scales

由图3可知，率定期作为率定模型的数据来源时期，其拟合效果最好，验证期为验证模型的准确性，其拟合效果略差，以季尺度数据源考虑气温的CAR(T)Q模型为例，率定期R2、Ens和RMSE分别为0.902、0.893和0.045 m，在验证期模型各指标精度分别下降了9.87%、11.49%和增加了25.00%，但预测曲线均很好地跟踪了观测曲线的变化趋势，3种时间尺度数据源模型预测精度均较好，模拟效果较差的月尺度数据源CAR(T)M模型的率定期R2和Ens均不小于0.771、RMSE为0.069 m，验证期预测结果相对差些，Ens为0.695。但是月度地下水埋深数据量多，能刻画年内的地下水波动，季度也能大体反映出地下水的波动特征，而年度则不能反映地下水年内的变化。总体来说3种尺度的地下水埋深模型预测性能都较好，模型较为稳定，可进一步应用于地下水埋深的预测研究。

3.3 不同时间尺度数据源地下水CAR模型的差异性分析

图4 不同时间尺度CAR(T)模型差异性分析Fig.4 Difference analysis of CAR(T) models at different time scales

为了探索不同时间尺度数据源地下水CAR模型的差异，并筛选出最优模型，将1999—2017年期间各因子数据按照月、季、年3种时间尺度建立CAR模型，通过对比不同时间尺度考虑气温的CAR(T)模型之间的精度，得出最优时间尺度模型。由图4可知，月尺度CAR(T)M模型的相对误差在-13%～11%之间，季尺度CAR(T)Q模型的相对误差在-4.8%～8.8%之间，年尺度CAR(T)Y模型的相对误差在-3.1%～4.0%之间。基于3种模型的拟合精度比较可知，拟合效果最好的CAR(T)Q模型的R2、Ens和RMSE较拟合效果较差的CAR(T)M模型分别提高了11.30%、11.86%和降低了32.35%。由图4d可知，灌域在月尺度的相对误差明显高于年尺度和季尺度，部分月份相对误差超过10%。即CAR(T)Q模型的拟合精度明显高于CAR(T)M和CAR(T)Y模型，CAR(T)Y模型次之，CAR(T)M相对最差。可能是因为地下水埋深变化在时间序列上呈现滞后性，比如气温因素，有研究表明气温的变化需要滞后46.5 d才能经土体传至潜水面[38]，此外，部分月份降雨量和引黄水量为零，控制因素减少，拟合结果出现误差，这也是基于月尺度的CAR模型拟合结果相对较差的原因。从而验证了应用季尺度进行地下水埋深动态变化预测拟合精度最高。

3.4 气温对冻融区地下水CAR模型的影响

为了探索气温对冻融灌区地下水埋深的影响，将不考虑气温CARQ、考虑气温CAR(T)Q和只考虑冻融期(12月—翌年4月)气温CAR(TF)Q的季尺度模型进行精度比较。由表2可知，CAR(TF)Q模型的R2、Ens、RMSE分别为0.941、0.940和0.044 m，CAR(T)Q模型和CARQ模型的R2和Ens分别降低了0.53%、0.64%和2.98%、3.09%，RMSE分别提高了4.55%和11.36%，可以看出，CAR(TF)Q模型略优于CAR(T)Q模型，明显优于CARQ模型。从而验证了仅考虑冻融期气温的CAR(TF)Q模型为最优模型。其主要由于冻融期气温对地下水埋深有很强的约束作用，加之引黄水量和降雨量对其约束作用减弱，所以加入气温对冻融期模型的拟合精度有所提高，而非冻融期气温对其约束力不强，主要影响因素为引黄水量、蒸发量和降雨量。可知此模型在引入数据时应注意其物理背景，而不是相关影响因子考虑的越多越好。

表2 季尺度数据源条件下不同气温因子CAR模型比较Tab.2 Comparison of different temperature conditions CAR model using quarter data

4 结论

(1)灌域地下水埋深与引黄水量、蒸发量、降雨量和气温呈显著相关性，不同时间尺度数据源的相关性由大到小依次为：年度、季度、月度。

(2)季尺度数据源CAR模型拟合效果明显优于月尺度数据源CAR模型和年尺度数据源CAR模型，年尺度数据源CAR模型拟合精度次之，月尺度数据源CAR模型相对较差。季尺度数据源CAR模型的R2、Ens和RMSE较月尺度数据源CAR模型分别提高了11.30%、11.86%和降低了32.35%。

(3)仅考虑冻融期气温的CAR模型优于考虑气温的CAR模型，不考虑气温的CAR模型拟合结果相对较差。冻融灌区最优地下水预测模型为仅考虑冻融期气温的季尺度CAR模型，模拟值与实测值的R2为0.941，Ens为0.940，RMSE为0.044 m。