冻结黏土开尔文与伯格斯蠕变模型分析

吴晓云，刘 爽

(安徽理工大学土木建筑学院，安徽 淮南 232001)

冻土是指温度不超过0℃的岩土类材料，即含有冰的岩石和土壤。冻土具有暖季融化冬季冻结的性质，温度变化会引起土体内部的冻融循环，从而使土体内部的孔洞、裂隙、开裂等缺陷加速发展。冻土在长期荷载的作用下会产生蠕变变形和应力松弛[1]。冻土强度受温度影响，温度越低内部未冻水的含量越少，冰胶结物强度变高，冻土强度也随之增强，使得其在荷载作用下具有显著的流变特性[2-3]。蠕变是冻土显著的特点之一，在人工冻结法施工中冻土通常处于高应力状态下，蠕变变形的研究有利于工程的安全可靠性评价[4]。

目前，冻土蠕变特性的研究在国内外已经取得很大进展[5]。主要的研究方法是通过蠕变实验建立蠕变本构模型，其中包括经验模型、流变模型和应力-应变-时间模型。经验模型基于试验，由于此模型参数少，物理意义不明确，从而难以推广[6]。流变模型中的元件模型具有直观、明确的优点，其中代表性的流变元件包括代表弹性的弹簧、代表粘性的阻尼器等。元件模型中常见的复合模型有开尔文模型、马克斯威尔模型、西原体模型和伯格斯模型等[7]，虽然描述蠕变的形式多样，但伯格斯模型被广泛应用。文献[8]将西原模型中的粘弹性元件替换成分数阶的Abel黏壶，有效地模拟了冻土在高应力作用下的加速蠕变。文献[9]基于伯格斯模型，利用模拟退火分数阶导数优化了参数，更好地模拟了冻土的蠕变。文献[10]研究了温度影响下的冻土蠕变试验，并分析得出了冻土的一维蠕变模型。冻土的蠕变受温度、含水率、土样的类型和土体所处的应力状态等因素的影响，其中温度对冻土蠕变的影响最为重要[11]。因此，本文重点讨论在不同温度下的冻土蠕变元件模型。采用黏弹性较大的冻结黏土作为试验试样，进行不同温度和不同加载系数下的单轴蠕变试验。基于粒子群算法优化参数，分别进行广义开尔文模型与伯格斯模型模拟人工冻土蠕变试验，与实际蠕变试验测量结果进行对比分析。

1 冻结黏土单轴蠕变试验

1.1 冻结黏土单轴抗压试验

试验采用某矿井深度15.0～41.9m的黏土，土样含水率为20%，试样尺寸为50mm(直径)×100mm(高度)。试验采用WDT-100型液压伺服人工冻土多功能试验机，试验中试件所受的荷载和产生的应变可以实时采集。

人工冻土单轴抗压强度试验将试样分别在-5℃、-10℃和-15℃温度下养护24h，每个温度做三个平行试验。得不同温度下的冻结黏土抗压强度，如表1所示。

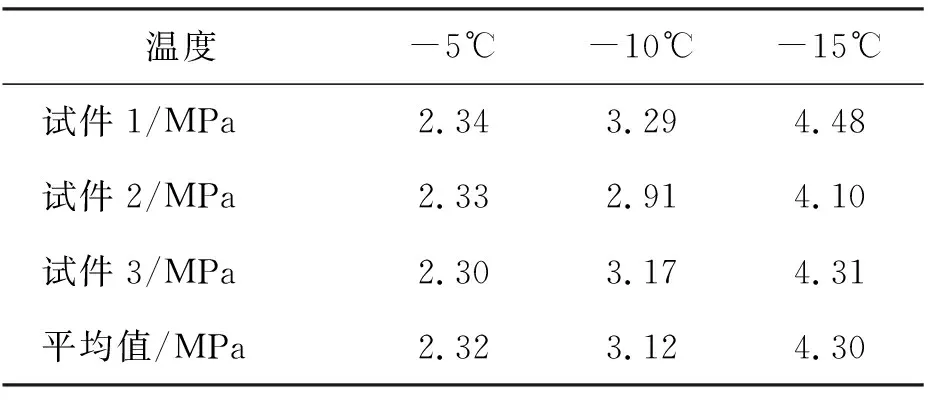
表1 冻土单轴瞬时抗压强度

人工冻土在不同温度条件下的单轴抗压强度受温度的影响呈线性变化，温度越低冻土的抗压强度越大。大量试验研究表明，人工冻土具有蠕变力学特性，且在蠕变时的应力-应变曲线呈抛物线分布[12]。本文研究中，不同温度下试样的应力-应变曲线关系如图1所示，重塑冻土在拐点后，应力增长速率随应变的增加而大幅降低。

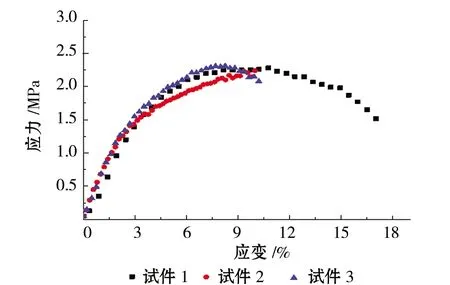
(a) 温度为-5℃

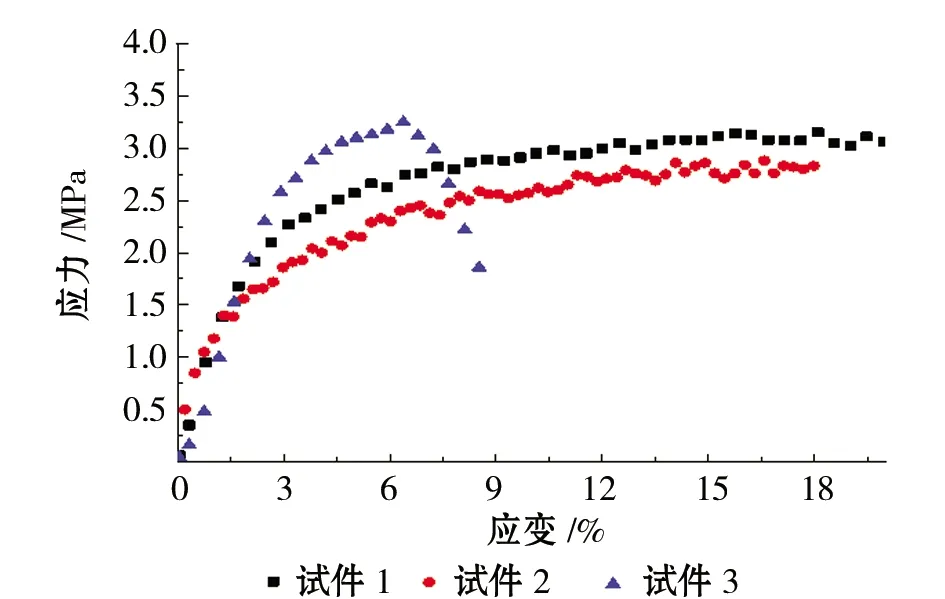
(b) 温度为-10℃

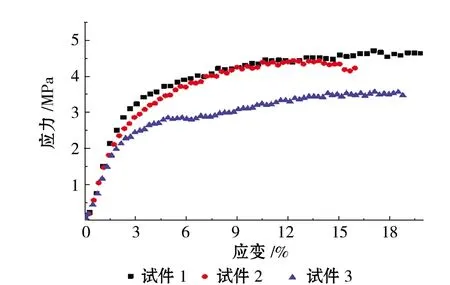
(c) 温度为-15℃图1 冻结黏土在不同温度下的应力-应变关系曲线

1.2 冻土单轴蠕变试验

冻土蠕变试验采用分级加载，加载等级分别为0.3σs，0.5σs,0.7σs，σs为瞬时单轴抗压强度。冻结温度分别为-5℃、-10℃和-15℃。试验依照国家标准进行[13]，每组三个试件不同的平均抗压强度计算得到的加载应力如表2所示。

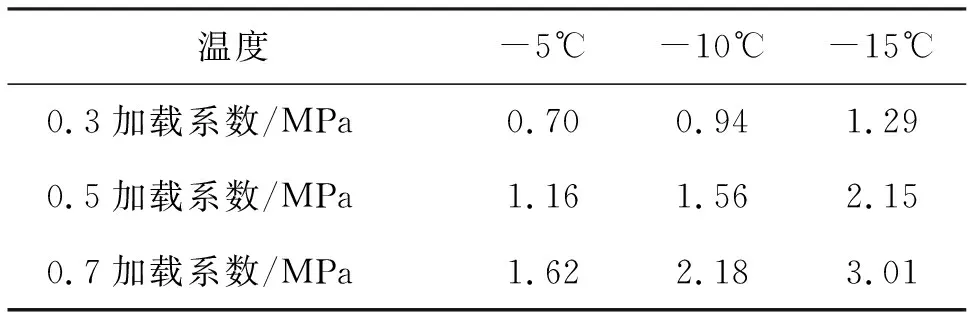
表2 冻土蠕变试验加载应力

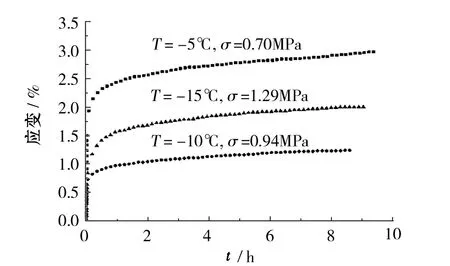
(a) 加载系数0.3

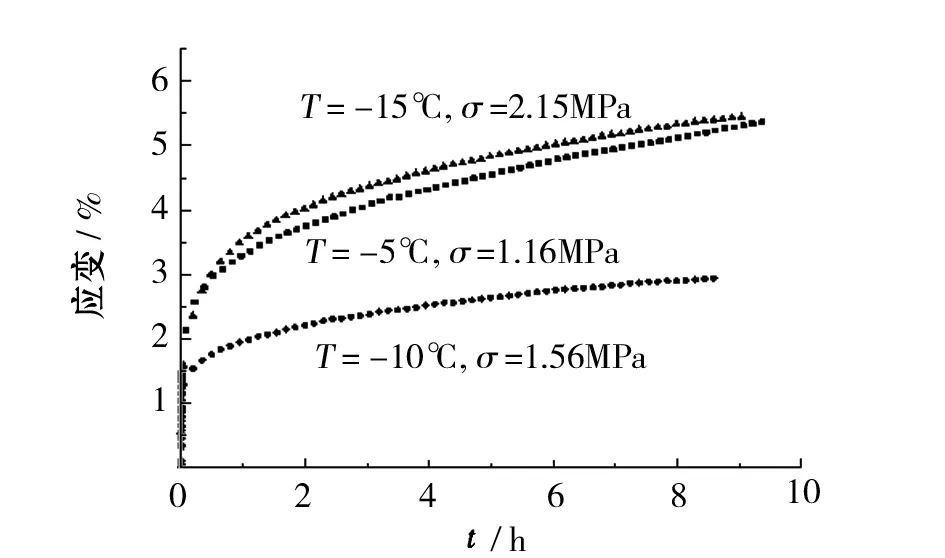
(b) 加载系数0.5

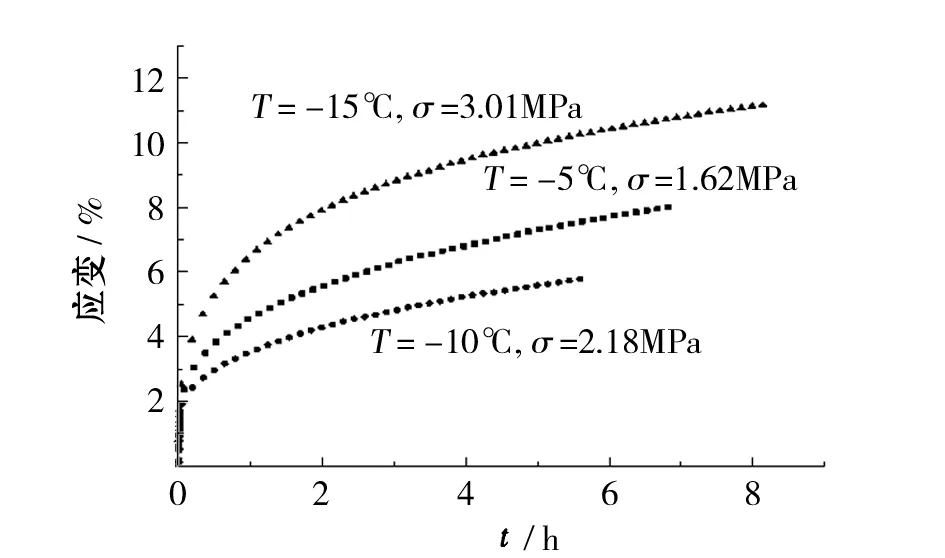
(c) 加载系数0.7图2 不同加载系数下的冻土蠕变曲线

不同加载系数下冻土蠕变曲线如图2所示，土样试样呈现由衰减蠕变阶段到稳定蠕变阶段的过程，变形限速到大体恒定不变。在稳定蠕变阶段冻土处于连续性未受破坏的黏性流动状态。由图3知同一冻结温度下的冻土蠕变由初始蠕变到常应变蠕变阶段的时间基本相同，如-5℃时，大约为2h。加载系数增加时，蠕变由初始蠕变到常应变蠕变阶段的时间减短。同温度下加载系数增加，冻土的稳定蠕变值也明显增加,在-10℃加载系数由0.3开至0.5蠕变值提升138%，-15℃时提升值是173%，可见在低温状态下增大加载系数对稳定蠕变值有显著的增加。

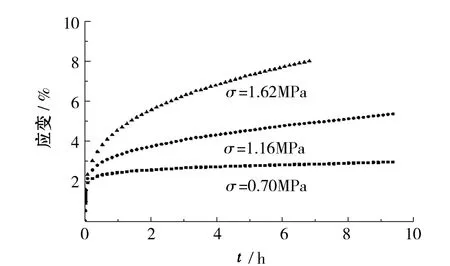
(a)温度为-5℃

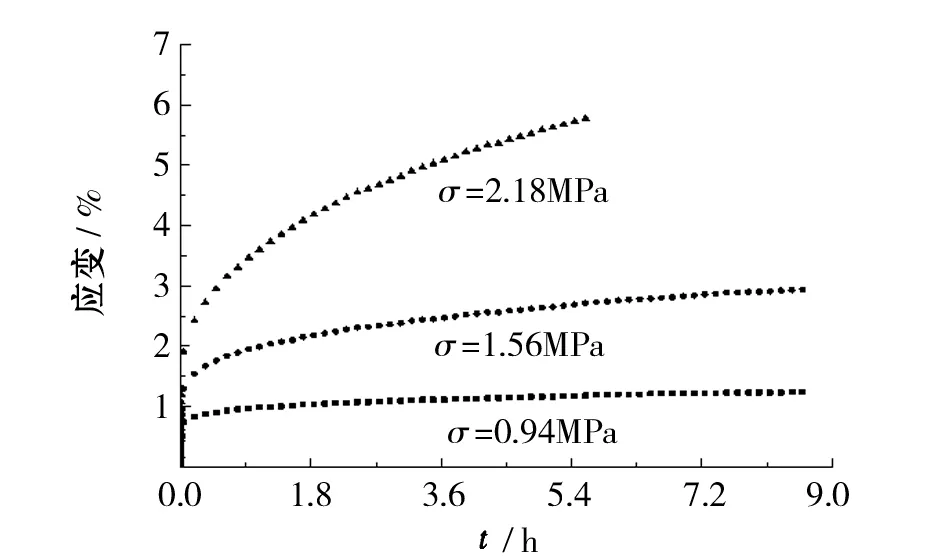
(b)温度为-10℃

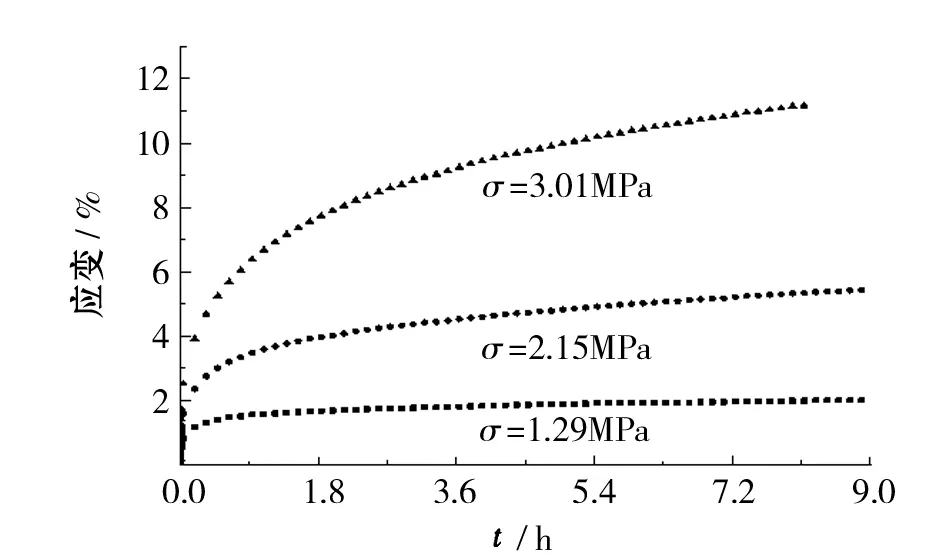
(c)温度为-15℃图3 不同温度下的冻土蠕变曲线

2 冻土蠕变元件模型分析

2.1 粒子群算法

有k个粒子组成一个群落在一个D维的目标搜索空间，Xi=[Xi1,Xi2,…,XiD]，Vi=[Vi1,Vi2,…,ViD]分别表示第i个粒子的位置向量和飞行速度，第i个粒子搜索到最优位置为Pi=[Pi1,Pi2,…,PiD],而Pg=[Pg1,Pg2,…,PgD]表示整个群体搜索到的最优位置，根据下列公式更新粒子的速度和位置。

Vi(n+1)=Vi(n)+c1r1[P1-Xi(n)]+

c2r2[Pg-Xi(n)]

(1)

Xi(n+1)=Xi(n)+Vi(n)

(2)

式中：c1,c2(>0)为学习因子，调节该粒子向自己寻找最优位置和同伴已寻找到的最优位置飞行的最大步长；r1,r2为0到1的随机数；n为迭代次数，即飞行步数。

在实际问题中，将V设定在一个范围[-Vmax,Vmax]，当粒子的飞行速度足够小或达到预设的迭代步数时，算法停止并输出结果[14]。

2.2 广义开尔文模型分析

开尔文体是一种黏弹性体，由一个弹簧与一个阻尼并联组成，再串联一个弹簧组成广义开尔文模型，参数物理意义明确[15]。广义开尔文模型的元件组成如图4所示。

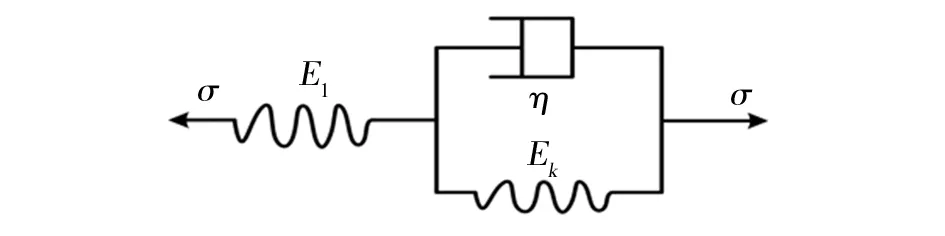
图4 广义开尔文模型

广义开尔文模型方程为

(3)

式中:E1为开尔文模型中弹簧的弹性模量；Ek为模型中并联弹簧的弹性模量；η为并联的黏壶的黏滞系数；t为时间。本次实验未采集到瞬时变形，故E1趋于无穷大。

分别将0.3、0.5和0.7三个不同加载系数实测蠕变结果带入粒子群算法，优化整理后的各温度下广义开尔文模型的参数情况见表3，温度和加载系数都对该模型参数有显著的影响，温度-10℃的冻土比-5℃时的并联弹簧弹性模量增大近一倍，增大加载也造成黏滞系数有明显的增加。

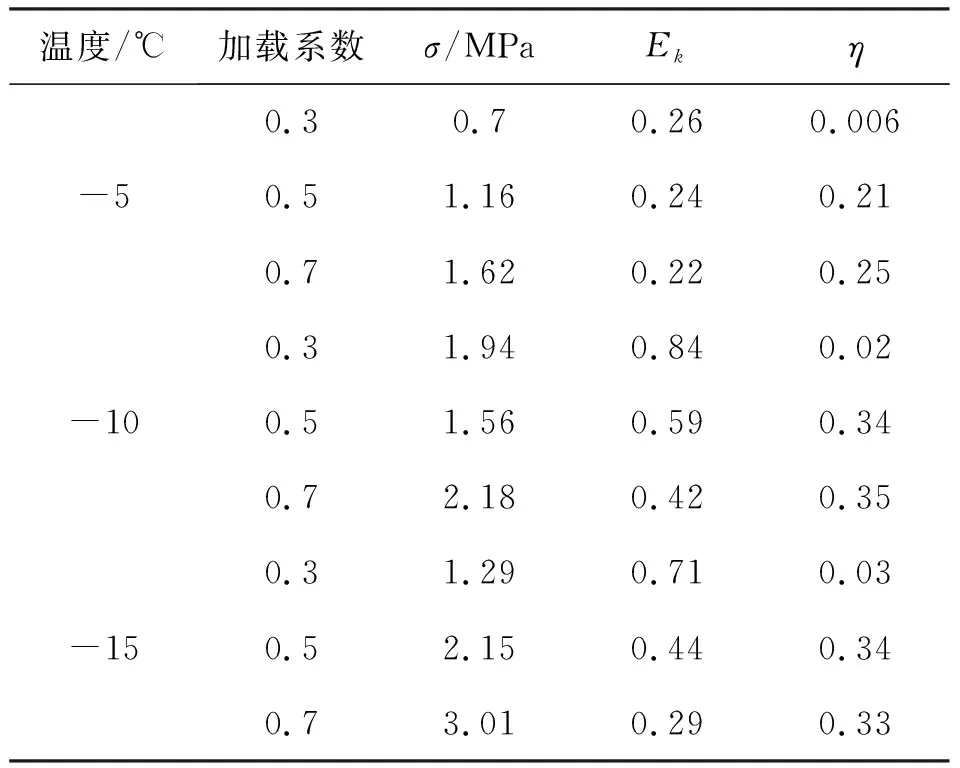
表3 广义开尔文模型冻土蠕变模型参数

2.3 伯格斯模型分析

伯格斯模型是目前常用在岩土蠕变变形研究中的模型，用来模拟岩土的蠕变过程[16]，考虑了冻土的弹性、黏弹性和弹塑性的力学特征，由开尔文体和马克斯威尔体串联组成如图5所示。

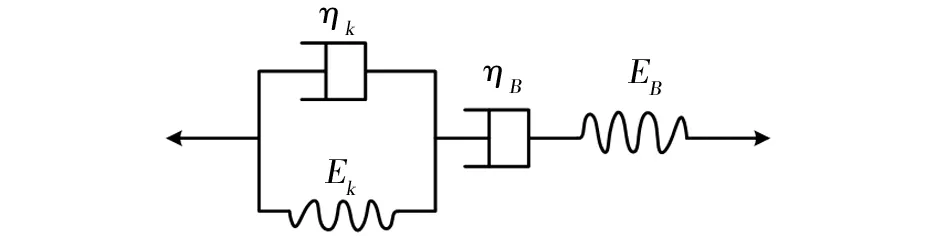
图5 伯格斯模型

伯格斯模型蠕变方程

(4)

式中：EB、ηB分别为马克斯威尔体中的弹簧的弹性模量和黏壶的黏滞系数；Ek为开尔文体并联弹簧的弹性模量；ηk为黏壶的黏滞系数；t为时间；σ为正应力。按照0.3、0.5和0.7三个加载系数实测蠕变结果通过粒子群算法优化整理后的各温度下广义开尔文模型的参数情况如表4所示。

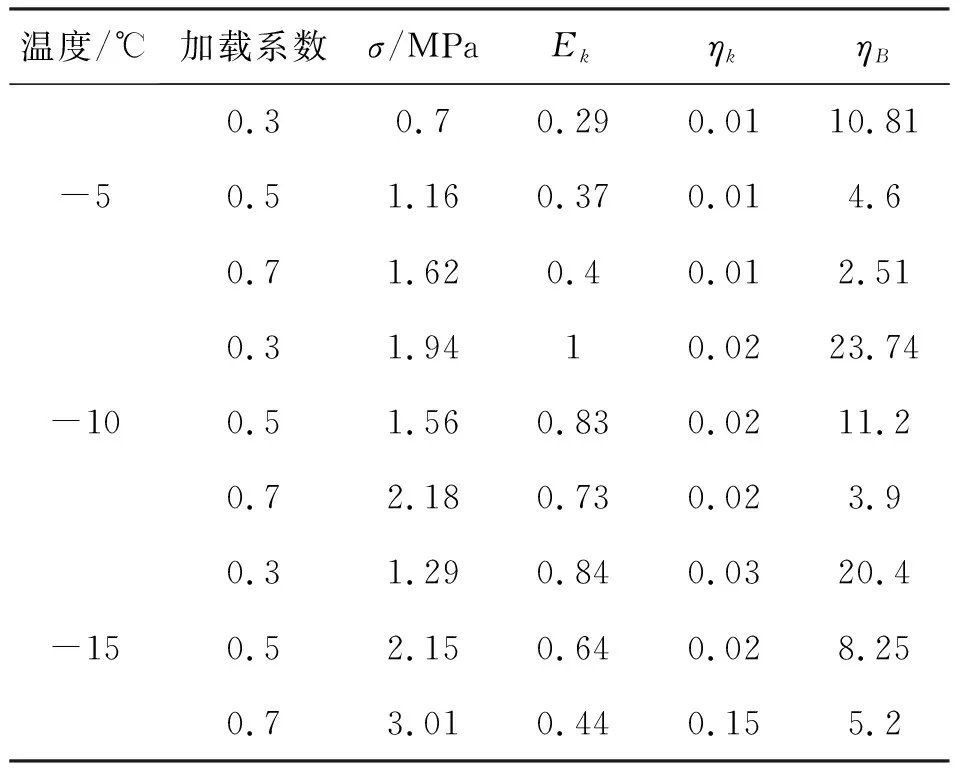
表4 伯格斯模型冻土蠕变模型参数

由表4知在伯格斯模型中的马克斯威尔体黏滞系数受加载大小的影响非常明显，开尔文体的黏滞系数受温度和加载系数的影响不明显，开尔文体弹性模量受温度影响较大，-10℃时比-5℃时值增大101%左右。

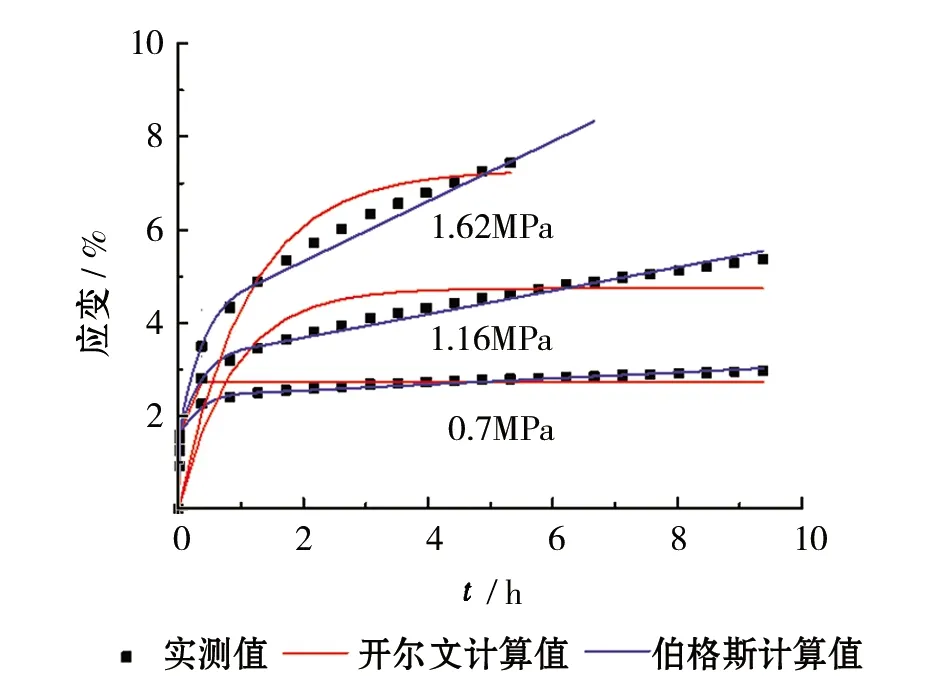
图6为广义开尔文模型与伯格斯模型模拟冻土蠕变与实际测量蠕变值的比较，由模拟结果可得以下结论。

1)广义开尔文模型在蠕变初始阶段的计算结果与实际测量结果有偏差，尤其加载系数较高时，冻土第一阶段初期蠕变的时间比实际要滞后。第二阶段稳态蠕变曲线斜率实际基本保持不变，而广义开尔文线斜率减小趋于直线。在加载系数较小的情况下，广义开尔文模型模拟蠕变变形的吻合程度较高，三个温度下的模型曲线与实测值相关系数达到0.94以上。

2)如图6伯格斯模型模拟蠕变曲线与实际测量蠕变值吻合效果较好，在蠕变的第一阶段与第二阶段模型计算值都可以很好地与蠕变曲线吻合，三个温度下的模型曲线与实测值相关系数达到0.98以上,高加载系数作用下的拟合稍有偏差但都较开尔文模型有很大提升。

(a)温度为-5℃

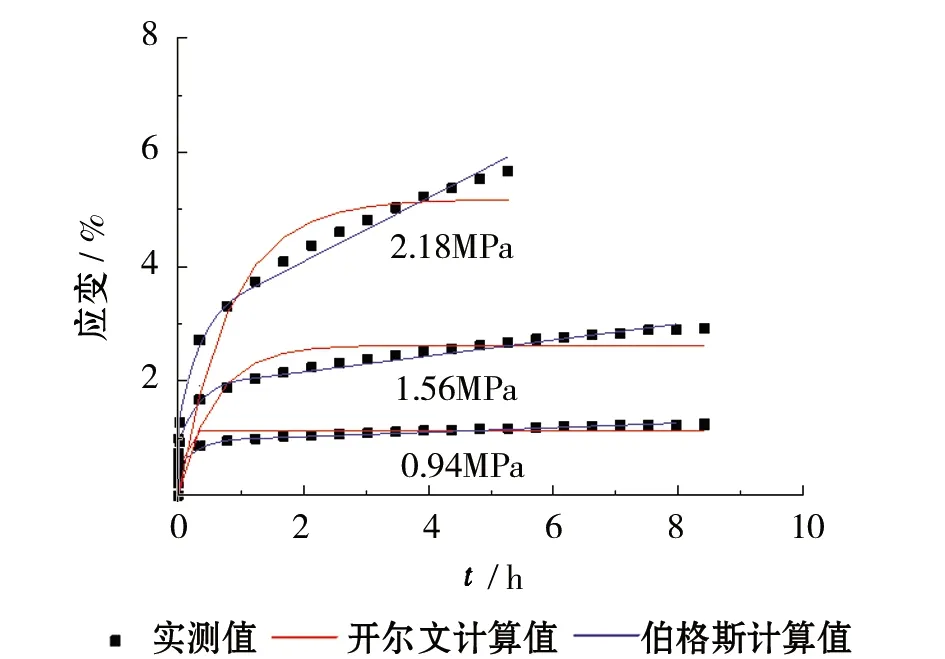
(b)温度为-10℃

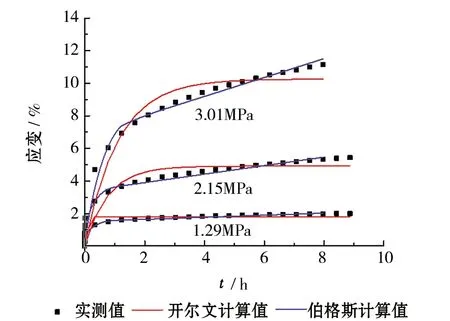
(c)温度为-15℃图6 开尔文模型和伯格斯模型计算值与测量值对比

3 结论

通过对不同温度下的人工冻结黏土进行不同荷载下的单轴蠕变试验，结合广义开尔文模型和伯格斯模型，采用粒子群算法优化模型参数，得到以下结论。

(1) 冻土的单轴蠕变试验同时受冻结温度和加载系数的影响。温度相同、加载系数增加时，冻土蠕变曲线稳定蠕变值显著增加。不同加载系数条件下冻土蠕变规律与冻结温度的关系复杂。在加载系数较高的条件下，温度越低稳定蠕变值有显著增加趋势，而在低加载系数条件下的稳定冻土蠕变值随温度降低的增加趋势并不明显。

(2) 加载系数较小时，广义开尔文模型预测结果较好，但无法描述人工冻结黏土的稳态蠕变阶段和加速阶段。而伯格斯模型可以预测不同温度和加载系数下的人工冻结黏土蠕变特性。