数线（数轴）在小学数学教学中的应用

【摘要】本文论述数线（数轴）在小学数学教学的应用策略，建议教师从最基本的“数线（数轴）”入手，从以“形”助“数”、以“数”解“形”两个方面，分析数学课堂教学中合理使用数形结合的方法。

【关键词】数线（数轴） 数形结合 以“形”助“数” 以“数”解“形”

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2020）06A-0092-02

《义务教育数学课程标准》（2011年版）指出，数学学习不仅仅是数学基本知识和技能的学习，还包括数学基本思想和基本活动经验的学习，强调学生经历知识的自主探索过程，在知识形成的过程中感悟和体会数学思想方法。数形结合思想正是其中一种重要的数学思想，它是通过数（数量关系）与形（空间形式）的相互转化、互相利用来解决數学问题的一种思想方法。数形结合，可将抽象的数学语言与直观的图形相结合，是抽象思维与形象思维的结合。对于小学生来说，思维正从直观形象思维向抽象逻辑思维的过渡，数形结合正是连接这个过程的纽带，作为最常见的“数线（数轴）”，则简单易懂，如果教师能够把它合理利用，就能使复杂的问题简单化、分散的问题集中化，让课堂教学变得事半功倍。

一、以“形”助“数”促理解

数学是抽象的科学，特别是对于部分抽象概念的理解，有的学生常常通过死记硬背来巩固。数形结合能为学生提供恰当的形象材料，把抽象的概念形象化，把复杂的数量关系具体化。

（一）“因数和倍数”教学设计

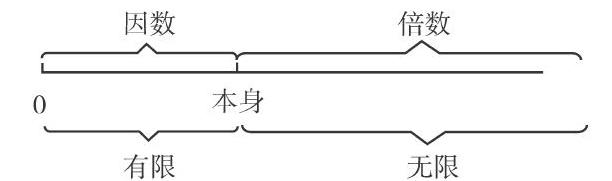
对于“因数”和“倍数”这两个概念，学生经常混淆。在教学中，利用画图表示的方法，能够让学生充分感知因数和倍数的含义以及它们的内涵和外延。从图中学生能清楚地看出因数的个数是有限的，范围从0至它本身，而倍数的个数是无限的，范围从其本身到无限大。通过数线图，学生形成清晰的表象，也对数轴有了更清晰的感知。

（二）“四舍五入法”教学设计

在求近似数时，教师一般会要求学生使用“四舍五入法”。通常教师会直接告诉学生什么是“四舍五入”，然后反复强调，练习巩固，但仍然会有不按套路出牌的学生。“四舍五入”这个词如此浅显易懂，学生为什么就是不会呢？经过思考，笔者把直观的数轴引入教学，让学生在数轴上找最接近的整十数，从而建立起直观的数学模型，加深对“四舍五入”的理解。

如求一个小数的近似数：“一个两位小数经过四舍五入后是3.2，这个两位小数是多少？”这类问题有些学生没办法清晰地理解题目的含义，本质也就是对“四舍五入”存在较大的困惑。因此，笔者采用竖向的数线，利用不同颜色的字体表示，把“四舍”和“五入”部分加以区分，让学生一目了然。

（三）“分段计费”教学设计

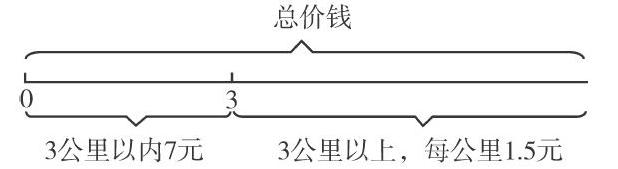
“某地出租车收费标准为‘3公里以内7元;超过3公里，每公里1.5元（不足1公里按1公里计算）。当行驶里程是6.3公里时，应付多少钱？”这是人教版（2011年版）教材中新出现的内容。教材采用了数据分析与表格分析的方法帮助学生理解分段计费的含义。

但在教学过程中，笔者发现学生并不能快速地解决问题：总的收费怎么求？每一小段的收费是多少？怎么求？经过思考，笔者采用以下数线图的方法进行教学。

通过数线图，学生能清晰地感受到总价钱就是要把两部分价钱加起来，如果还有第三次分段，就把三次分段的结果分别求出再加起来。这样的数线图学生比较容易画出来，也比较容易理解，进一步降低了学习的难度，学习效果比较好。

虽然以“形”助“数”，把数转化为易观察、易理解的图形，促进了知识的理解，但“形”是过程，“数”才是结果，因此，教师还要对知识进行总结、梳理，并加以灵活运用，让“数”变成“形”后能够再回到“数”的运用中。教师可以根据教学内容和学生的年龄段选择表达、复述、练习等方法。如在“因数与倍数”教学中，笔者让学生结合例题，通过复述分析的方式，加深对新知的理解。而在分段计费的教学中，笔者则在练习中通过设计三次分段计费的问题，让学生再次画图、深入解决，从而提升对“数”的理解。

二、以“数”解“形”拓思维

以“数”解“形”的学习方法一般多运用在初中和高中的数学教学中，通过“数”可以帮助学生解决复杂的“形”的问题。其实在小学阶段，有些教学内容也可以充分利用“数线（数轴）”，通过“数”来解“形”。

（一）发展思维时

在解决问题时，教师常常因为学生对于题意的理解不透彻、不全面感到头疼，特别是年级越高、条件越复杂的时候，部分学生更是“无从下手”。此时，如果把条件变成直观的数线（数轴），通过图形、表格、数量之间的互相转化，就能促进学生理解题意，发展学生的思维。

例如，在“植树问题”教学中，学生对100米道路上种树的问题进行“猜测”后，教师让学生进行“验证”，可是100米太长了，不好画图，于是教师让学生“化繁为简”，经历两个层次探究植树问题的规律。

第一个层次：在20米的道路上，每隔5米种1棵树，（两端都种）可以种几棵？

学生利用线段图来呈现自己的想法，师生共同小结得出：棵数=段数+1（两端都种）。

第二个层次：自己选择一段道路进行种树，采用画线段图的方式解决问题。

通过学生独立作图、汇报、展示，再一次验证了规律所在。

把条件变成数线图，通过“数”与“形”不断地转化，让学生的思维发展有了凭借，由“形”的直观变为“数”的严密，由“数”的严密联系到“形”的直观，进而促使数学思想方法真正得以渗透。

（二）整合知识时

数学知识不是孤立存在的，它们之间存在严密的内部联系，从低年级向高年级螺旋上升。教师应该利用有效的迁移，让学生系统地将其整合，形成数学知识网络。

如“分数的意义”教学设计环节，教师就充分利用有效的迁移引导学生系统整合数学知识。

师：同学们，你们能用“1”来表示以下的事物吗？

（教师出示图片：1个苹果、1群马、1间教室、1个班的同学）

师：你还能举例出像上面这样的生活中的“1”个事物吗？

生1：1块蛋糕。

生2：1个小区。

……

师：我们把这些“1”用单位“1”来表示。你们知道为什么“1”要加引号么？（不只表示1个，还可以表示1群）

师：是啊，单位“1”可以表示1个物体、1堆物体、1个计量单位……

数学具有“简洁”之美，教师不仅可以把各种因素转化为数学知识，还可以让学生了解数学的发展历史。自然数、分数、小数等知识都是人们从日常生活中逐步提炼出来的，通过从学生熟悉的感性材料入手，利用学生已有的“1”的概念，抽象出单位“1”的概念，从“形”上抽象出“数”，让学生从内在意义和外在表现上初步感知单位“1”。接着，设计在图形中找分数的练习，利用数轴理解2、3、[12]、[14]……进一步加深学生对分数的理解，进而对“数”也有了更深刻的理解。当然，在以“数”解“形”的过程中，教师要注意避免“数”的枯燥，在提炼出“数”后，还要和“形”加以联系，从而提高理解知识的实效。

“数”“形”结合、互化的过程，既是知识生成的过程，又是学生的形象思维与抽象思维协同运用、互相促进、共同发展的过程，只要我们合理地使用数形结合思想，就能使我们的教学更加富有魅力，使我们的课堂更加高效。

作者简介：施慧敏，女，福建省优秀教师，厦门市数学骨干教师，现任厦门市江头第三小学教学副校长，主要从事小学数学教育教学工作。

（责编 林 剑）