横看成岭侧成峰 远近高低各不同——坐标法解决平面向量的模长问题

卢会玉

(甘肃省嘉峪关市第一中学 735100)

以平面向量模长为背景的综合题，通常与函数、不等式、平面几何、三角函数、解析几何等知识点结合考查，能综合考查学生分析问题和解决问题的能力，能有效考查学生的思维品质和学习潜能，体现了高考在知识点交汇处命题的思想，是高考的热点，也是难点. 解决这类问题的关键是认真分析题意，恰当地将问题等价转化为解析几何中的模型，或者函数或不等式求最值等问题进行求解.

正因为向量既有“数”，又有“形”的双重身份，所以数形结合法是解决平面向量模长问题的常见方法．而坐标法作为学生非常熟悉的方法，自然而然成为了平面向量模长的解题利器，这也是一种将几何问题代数化的典范.

一、已知向量坐标求模长的问题

已知向量坐标求模长的问题常与二次函数的最值或者三角函数的范围有关，运算正确即可.

例1已知向量a=(1-t,t),b=(2,3)，则|a-b|的最小值为( ).

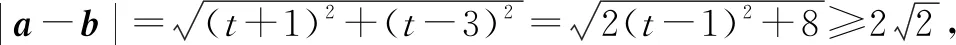
故选C.

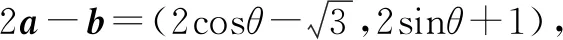
二、已知条件中有明显垂直关系的模长问题

有一类在已知条件中有明显的垂直关系的问题，比如已知矩形、数量积为零等等. 这类问题很多学生是可以想到用坐标法的，建立直角坐标系后，剩余的问题就是运算.

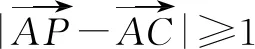
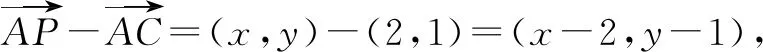
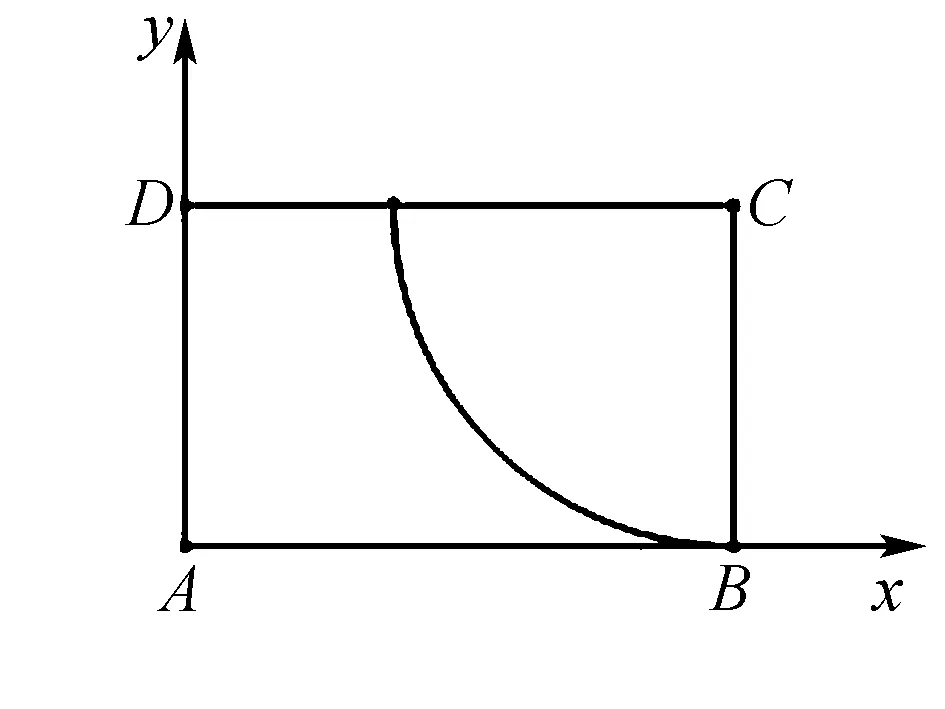
图1

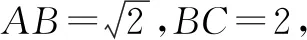
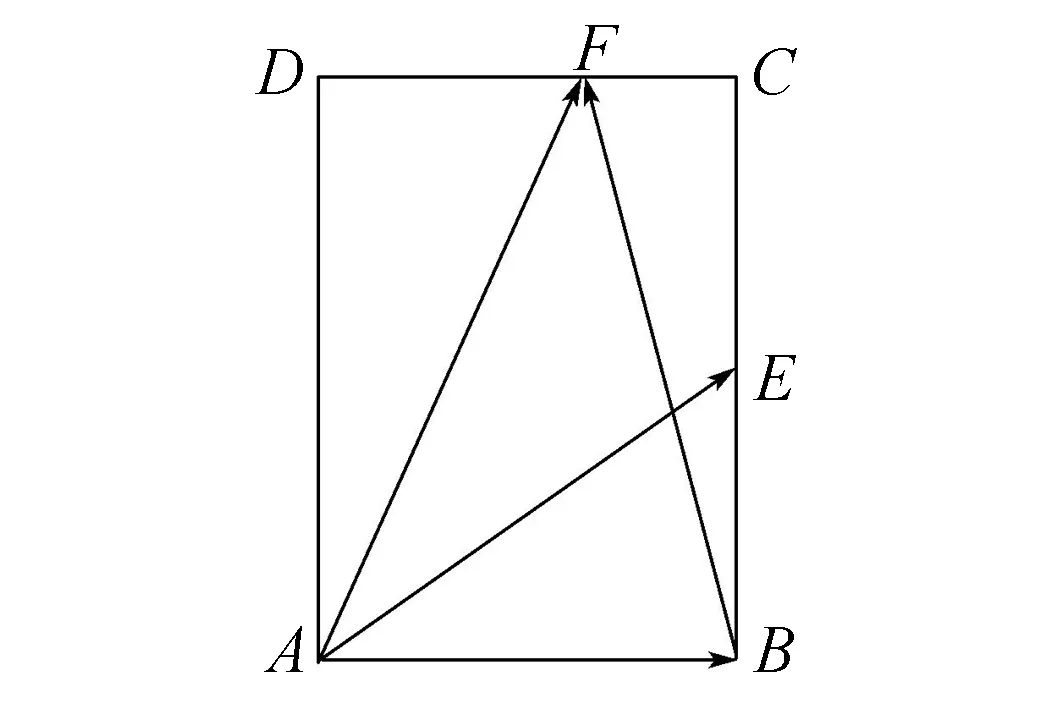
图2

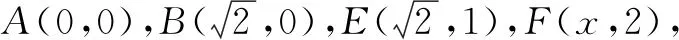
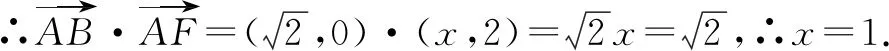
例5已知a,b是单位向量，a·b=0，若向量c满足|c-a-b|=1，则|c|的最大值是____．

解析因为a,b是单位向量，且a·b=0，所以可设a=(1,0),b=(0,1),c=(x,y),则c-a-b=(x-1,y-1).由|c-a-b|=1得(x-1)2+(y-1)2=1，即(x,y)的轨迹是以(1,1)为圆心，半径为1的圆.

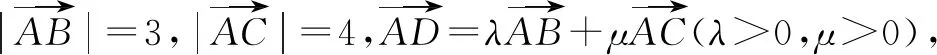
解析由题意可知，不妨以A坐标原点，AB所在的直线为x轴，AC所在的直线为y轴，建立直角坐标系，则A(0,0),B(3,0),C(0,4).

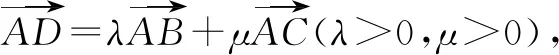
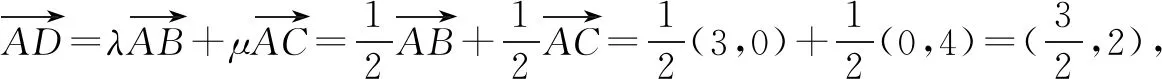
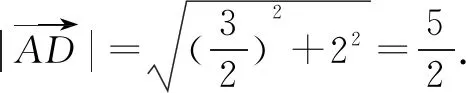
故选D.

三、已知条件中未出现明显垂直关系的模长问题

已知条件中未给出明显垂直关系的问题是比较常见的，那么如何透过现象，找到建立直角坐标系的契机，这就需要认真分析题目已知条件，难度较大.

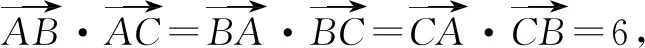
A. 3 B. 4 C. 8 D. 16

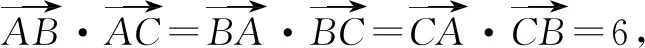
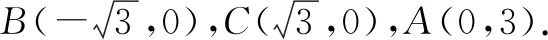
故选B.

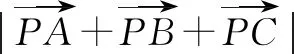
A．6 B．7 C．8 D．9

故选B.

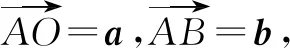
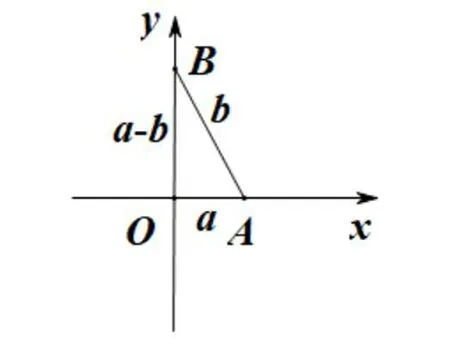
图3

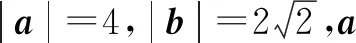
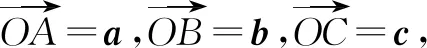
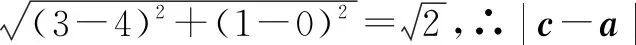
例11已知向量a,b，且|b|=2，b·(2a-b)=0，则|tb+(1-2t)a|(t∈R)的最小值为____．

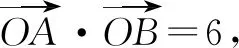
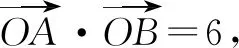
平面向量问题总是给人一种“横看成岭侧成峰，远近高低各不同”的感觉，但是不论平面向量问题是以何种方式呈现，不论和哪些知识进行交汇，首先应该去思考能否进行坐标法解答. 坐标是向量进行代数化的中传媒介,通过向量的坐标表示可将向量问题转化为代数问题来解决.而坐标是需要借助于直角坐标系的，所以对于某些平面向量问题,若能建立适当的直角坐标系,就可以使图形中复杂的几何关系转化为简单直接的代数关系.虽然存在运算问题，但是大大减少了推理过程,有效地降低思维量,起到事半功倍的效果．

上述问题几乎都是通过建立坐标系将向量问题转化为函数与不等式问题求解,体现了向量解题的工具性. 建立直角坐标系的原则是能准确快捷地表示有关向量或点的坐标，正确找到变量间的关系，以及正确分析目标函数代表的几何意义．