标准椭球面坐标系的建立及在各向异性电磁介质中的应用
许景生, 李文略
(岭南师范学院 基础教育学院,广东 湛江 524037)
陈燊年等[1]系统地研究了介质为各向异性(限于有且只有3个正交主轴方向的各向异性电磁介质)的电磁场,其中给出了各向异性电磁介质的边值关系,并得出了在电磁介质分界面为平面时,边值关系在空间直角坐标系下的具体形式,而对当分界面为其他形状时边值关系的具体形式没有作进一步的研究。由唯一性定理,一个电磁问题的完整描述应包含所满足的微分方程和相应的边值关系,且选择合适的坐标系会使描述的电磁问题简单化。李洲圣等[2]系统地定义了张量分析的矩阵方法,文献[3-8]应用该方法对各向异性介质的电磁场作了一系列的研究,为继续丰富各向异性介质电磁场的内容且使研究的第二边值关系问题更具典型性,本文应用张量分析的矩阵方法建立标准椭球面坐标系,并推导当电磁介质分界面为椭球面时,第二边值关系在标准椭球面坐标系下的具体形式。
1 应用张量分析的矩阵方法建立标准椭球面坐标系及相关的特征参量矩阵
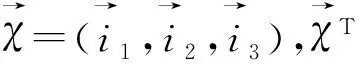
(1)
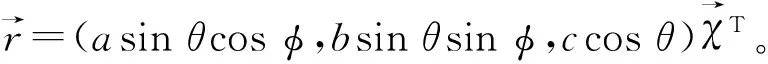
(2)
现计算协变六面体体积Ω,计算过程如下
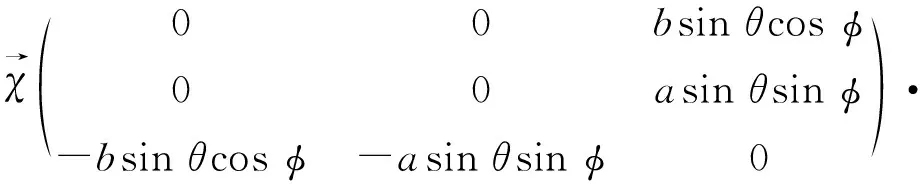
(3)
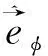
(4)
其中,▷11=a2cos2θcos2φ+b2cos2θsin2φ+c2sin2θ,▷12=b2sinθcosθsinφcosφ-a2sinθcosθsinφcosφ,▷22=a2sin2θsin2φ+b2sin2θcos2φ。由▷12≠0可知,当地标准椭球面坐标系的坐标标架是非正交的。在此需要进一步说明的是,文中建立的标准椭球面坐标系是非正交的,与传统的旋转椭球坐标系是不同的[9]。旋转坐标系是三维的正交曲线坐标系,尽管退化为二维的正交曲线坐标系,亦是不同于本文所定义的标准椭球面坐标系的。
2 各向异性电磁介质的第二边值关系
由电动力学或电磁理论可知,在各向同性电磁介质中,两种介质分界面处,场量满足的第二边值关系为
(5)

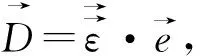
(6)

各向异性电磁介质边值关系式(6)中的第一、三式是二阶张量方程,第二、四式是矢量方程(1阶张量方程)。由张量方程的协变性,可应用张量分析的矩阵方法分别推导出磁各向异性介质和电各向异性介质第二边值关系在标准椭球面坐标系下的具体形式。
3 标准椭球面坐标系下各向异性磁介质的第二边值关系
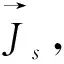
边值关系式(6)中的第一式用张量分析的矩阵方法计算,
(7)
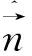
(8)
式(8)即为第二边值关系式(6)中第一式在标准椭球面坐标系下的具体形式,其中
(9)
由式(6)第二式得B1n-B2n=0,该关系式与式(8)(9)构成了当各向异性磁介质的分界面为椭球面时,第二边值关系在椭球面坐标系下的具体形式。可知,各向异性磁介质的边值关系很繁琐,以下对该边值关系进行讨论。
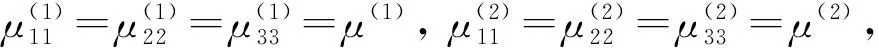
(10)
4 标准椭球面坐标系下各向异性电介质的第二边值关系
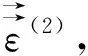
边值关系式(6)中的第三式用张量分析的矩阵方法计算
(11)
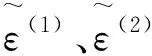
(12)
其中,
(13)
边值关系式(6)中的第四式用张量分析的矩阵方法计算
(14)
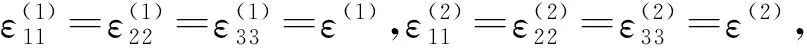
(15)
所得结果与文献[10]一致。
5 结语
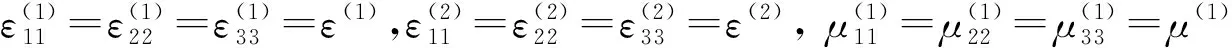
由于各向异性电磁介质第二边值关系是张量方程,它具有协变性,故可应用张量分析的矩阵方法得到该边值关系在标准椭球面坐标系下的具体形式。各向异性电磁介质边值关系的协变性有助于加深对各向异性电磁介质介电属性和磁导属性的理解,以及由此推导出第二边值关系的具体形式,可作为研究各向异性电磁介质电磁属性基础理论的补充。

