计算教学不仅仅是计算

莫国平

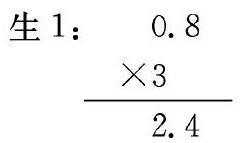
摘 要：随着计算器和计算机等电子计算工具的普及，大数目的精确计算完全可以借助这些工具方便地完成。因而，我们现在使用的国标本教材中相应地减少了大数目的繁杂计算，降低了对计算熟练程度的过高要求，并且把计算教学作为解决问题的一个组成部分，这是小学数学课程改革的一个亮点。对于此，我们的计算教学要立足于解决问题的高度去审视，要自觉摒弃让学生机械模仿、反复操练，进而掌握算法使计算熟练的传统教学观念，而要让学生的学习成为“一个生动活泼的、主动的和富有个性的过程”。

关键词：计算数学;机械模仿;生动活泼

中图分类号：G623.5文献标识码：A 文章编号：1992-7711（2020）13-092-2

国标新教材减少了大数目计算，降低了对学生计算过高的要求。在这种情况下，教师如何把计算教学有机融入问题解决的过程之中，从而使我们的计算教学更符合课程标准的理念？笔者结合一节计算课的教学实践，谈谈自己的一些想法。

【教学片断】

师：你从情境中获得哪些数学信息？

生1：夏天，西瓜每千克0.8元。

生2：冬天，习惯每千克2.35元。

师：根据这些信息，你能提出数学问题吗？

生1：冬天的西瓜比夏天的贵多少元？

生2：夏天买一个西瓜要多少元？

师：假如买一个3千克的西瓜要多少元？你会列式吗？

根据学生回答板书：0.8×3

师：你能估算一下，大约是多少元吗？

生：大约是3元。

师：怎么估算的？

生：0.8元接近1元，1乘3等于3。

师：你能精确地算出是多少元吗？

生1：0.8元就是8角，8角乘3等于24角，24角就是2.4元。

生2：0.8×3就是0.8+0.8+0.8，等于2.4元。

师：你会列竖式计算吗？请你尝试一下。

师：有不同的竖式吗？

老师展示另一个学生的竖式：

师：在列竖式计算小数乘法时，我们确实要小数看作整数列竖式，也就是看作8×3，所以这位同学的竖式是正确的。

师：那积的小数点为什么要点在2和4的中间呢？

生：因为小数点要对齐。

师：哦！与哪个数的小数点对齐？

生：与0.8的小数点对齐。

师：谁有不同的想法吗？

生：那为什么积的小数点不与3的小数点对齐呢？

师：对啊！在加减法中，我们要求所有的小数点对齐。但在乘法中显然不是这样的，因为3的小数点就没有与0.8的小数点对齐。

生：因为因数中有一位小数，所以积也是一位小数。

师：是啊！因为0.8×3看作8×3，0.8扩大10倍，因为24要缩小10倍就是2.4。

师：刚才我看见一位同学计算时，开始的积是24。后来又改了，我想知道当时他怎么想的？

生：因为我想到开始估算时，积大约是3，而不可能是24，所以改成2.4。

师：好的。看来估算还可以帮助我们检验计算得是否正确呢！

师：当我们计算好了，应该怎么办？

生：验算。

师：怎么验算？

生：可以交换乘数的位置验算，也可以用除法验算。

师：现在还没有学习小数除法，所以请同学们用乘法验算。

【教学反思】

一是要突出培养学生的“问题意识”

问题是指“对学生来说没有现成方法可以解决的情境状态”。“有没有现成方法可以解决”突出了问题本身的挑战性，这也是判断一个问题能否成为“问题”的关键。但是，所要解决的“问题”从何而来？是由教师指令性的给出问题，还是引导学生自己发现并提出问题？显然我们追求的应是后者。在教学中，我们期望通过创设一定的情境，引导学生自觉地用“数学的眼光”发现并提出问题，从而逐步培养学生的问题意识。因此，我在课的一开始出示了课本中的情境图，这是学生非常熟悉的生活情境，学生觉得真实而亲切，具有强烈的现实感，同时在解决问题的过程中，学生体验了计算的应用价值，充分体现计算教学的价值。

我出示了学生熟悉的情境，没有出示课本上的现成问题，而是给学生留下了自主提问的空间，让学生用数学的眼光去发现与思考，从而自主提出数学问题：冬天的西瓜比夏天的贵多少元？夏天买一个西瓜要多少元？这样的教学不仅较好地引导学生提出了问题，并且学生在提出问题时已经自觉地产生了主动探索计算方法的需要。这样的情境创设才不会为了情境而情境，这样的情境才有意义。

二是要突出培养学生的“探索意识”

课程标准指出：有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学额重要方式。因此自主探索是学习数学的重要方式，也是学习的过程性目标之一。学生对计算方法的理解和掌握应建立在自主探索的基础上，不能停留在记住所谓的“法则”，然后让学生搬硬套、重复练习。

情境本身提供的是现实生活的问题，较好地激发了学生探索计算方法的需要，这种内部驱动产生的热情是维持学生深入探索的“助推剂”。在学生面临0.8×3这个新的计算时，所有的探索活动都是建立在原有的认知发展水平（整数乘法和元角之间的转换）和已有的生活经验（在日常生活购买东西的经验）基础之上的。当然这个知识的“脚手架”会随着学习经验的积累，他们会逐步学会建立适合自己的“脚手架”，而对于探索能力弱的学生，可能教师要主动伸出“援助之手”。在经历探索的过程之后，我引导学生开展回顾、反思的活动，有条理地梳理思考的路线，深入认识自己成功的策略或失败的原因，发展解决问题的策略，强化情感体验。成功的探索过程，会留给学生的是无比愉悦的情感体验和进一步探究的动力。

三是要突出培养学生的“交流意识”

“由于学生所处的文化环境、家庭背景和自身思维方式的不同，学生的数学学习活动应当是一个生动活泼的、主动的和富有个性的过程。”对于本课的小数乘整数的计算方法的探索，不同的学生会充分利用自己的生活经验和学习经验，从不同的角度探索解决问题的方法，因而在小组内或班级内形成算法多样化的局面是一种必然现象。这时，学习同伴间的交流就非常有必要。当学生独立思考后我引导学生交流，在交流中学生深化了自己对问题的理解，同时也认识、借鉴他人的合理方法，从而找到最适合自己的方法。

当然，交流的重点既要关注探索的结果，更要关注探索的过程。当老师问“为什么积的小数点点在2和4的中间？”时，有学生认为是小数点对齐，但马上有学生反驳了对方“那积的小数点为什么不与3的小数点对齐呢？”这是多么有力的反驳啊！只有关注了过程，我们的教学才会变得睿智而灵动。这样的交流，有助于学生在独特体验的基础上建构合理的计算方法。

四是要突出培养学生的“验算意识”

教师要重视培养学生验算的意识，督促学生自觉“反思结果的合理性”。不少学生认为验算没有必要，验算是为了完成课本的要求或者应付教师的检查，自觉验算的意识非常薄弱。学生在紧张的计算后肯定关注结果是否正确，教师要把握学生此时的心理，引导学生自己进行验算。通过验算发现学生计算中出现的错误，从而体会验算的价值。

验算还是一个再学习的过程，学生在验算的时候，方法也是多样的。有的重新算一遍，有的根据运算之间的关系来验算，有的用估算来“监控”结果的范围，这些方法都是很好的再学习的过程。同时验算也是培养责任感的途径，具有良好验算习惯的学生都是责任心很强的学生。通过验算，培养学生做事有始有终，对自己的行为负责的良好态度，这也是不容忽视的。

问题意识、探索意识、交流意识、估算意识、验算意识是学生数学素养的重要表现，形成這些素养需要长期的过程，并且要和具体的教学过程水乳交融。如果脱离具体的情境，孤立地强化某方面的意识，期望毕其功于一役，教学的效果可能适得其反。

（作者单位：苏州市吴江区松陵小学，江苏 苏州215000）