基于平滑反射运动的工业机器人多变量时间最优轨迹规划研究*
刘兰兰,邱 磊
(1.江西制造职业技术学院 机械工程系,江西 南昌 330095;2.宁波工程学院 机械工程学院,浙江 宁波 315336)
0 引 言
在高精度装配行业中,重复性和速度之间的均衡是机器人的关键竞争优势,特别是机器人在执行高精度装配任务时需要具备非常高的运动平滑度[1-4]。传统的工业机器人轨迹规划研究[5-7]主要是从时间、运动平滑度或两者的结合展开分析。在精密制造领域,运动平滑度是主要的考虑因素。
针对上述问题,许多研究依赖于使用经各种方法优化或约束的样条函数[8-9],或者在操作工作空间对多轴运动进行管理[10-11],例如在某些情况下可对关节空间中的轨迹定义进行简化,以便实现更平滑的连接轨迹。
在这两种情况下,很多研究人员都提出通过增加路径或运动轨迹的多项式来实现最优规划。例如,PERUMAAL S等人[12]通过一种运动同步策略(所有关节都以相对保守的方式将其加速率同步到最慢)进行了非多项式平滑性轨迹规划;张程等人以5-DOF仿人型机械臂为研究对象,建立了机械臂运动学方程,并实现了关节空间轨迹规划;LANGE F等人[13]针对一种空间3自由度并联机器人,提出了一种近似时间最优策略的平滑轨迹规划算法。该方法将运动学和动力学约束条件转换为伪速度极值曲线,保证了驱动力矩、关节速度和加速度的连续性。此外,机器人运动能力的进一步提升也受到了伺服驱动器的限制。因此,不能使用基于时间优化的再生运动策略来缓解机器人的退化现象。
在上述文献中,正弦运动曲线已应用于多个关节运动。但是,在多数方法中,所有轨迹阶段(加速度、恒定速度和减速度)在各关节上实现同步,即它们同时开始也同时结束。此外,现有多数方法通过单独评估其最快的加速斜坡时间和恒定速度时间,并使所有值等于最大值来确定所有关节的加速度/减速度以及恒定速度时间。这种保守标准与最优性相差甚远。
在平滑加加速度运动轨迹的基础上,笔者提出一种用于运动规划的多变量时间优化方法。
1 轨迹规划方法
在加速度、速度和加加速度的约束条件下,通过在关节空间中生成轨迹来对执行时间进行优化。考虑到运动的起点和终点坐标,参数运动曲线选择了正弦曲线,该正弦曲线适用于多关节运动。该参数系列允许生成平滑的运动曲线,同时提供一种简单的方法来控制加加速度、加速度和速度的最大值。研究表明想要确定三维空间中某一物体的位置的话,需要6个自由度(3个平移,3个旋转),如果机械臂具有6个自由度,那么它就能达到包络轨迹之内的任何一点,从而模仿人体关节完成三维空间中的任何动作。
笔者采用的6自由度(DoF)拟人化机械手如图1所示。

图1 6自由度(DoF)拟人化机械手
引入轨迹规划模块依赖于以下假设:
(1)所考虑的机器人机械手主要执行与组装过程相关的拾取和放置任务,其中需要非常平滑的拾取和放置运动,以实现被抓握部件的准确定位;
(2)在预拾取和预放置位置之间执行快速运动,不需要在笛卡尔工作空间中有特定路径(例如线性)或避免任何障碍物。这意味着可以通过在关节空间中进行轨迹设计,来执行快速点对点运动;
(3)虽然研究对象为球形腕部的6自由度(DoF)拟人化机械手,但所提出的运动规划方法具有通用性。
1.1 高精度机械手模型原理
工业机械手结构是由许多形成运动链的模块化关节和环节组成的。各关节i=1,…,n,其中:i—运动链中的序列位置,以特定关节类型ki为特征。通过使用两种不同类型的关节,可组装成一个典型的拟人化球形腕部结构,其中k1,k2,k3=1,k4,k5,k6=2。根据关节类型及其在运动链中的位置,每个关节具有不同的速度、加速度和加加速度。
组装任务的具体类型以及起始位置和结束位置也会影响各个关节的运动参数:例如,搬运组件时,可以较高的速度和加速度利用空夹具执行运动;此外,对于制动器而言有压力的长距离轨迹可能需要较慢的运动,以便将振幅控制在所需规格范围内。任务指数(m=1,…,nt)用以区分工作过程中不同部分之间的控制参数。
如上所述,该指数取决于开始和结束的笛卡尔位置ps、pe和任务类型h(拾取、放置、变更工具等),任务指数影响运动约束的值(最大加加速度JMAX,最大加速度AMAX、最大速度VMAX以及路径目的地),而加速曲线将针对各项任务进行优化。
1.2 正弦曲线运动轨迹数学表达式
研究人员必须使用适当的运动学倒位将位置ps和pe转化成各个关节的起始位置和结束位置,以便生成关节运动曲线。
为了生成关节运动轨迹,笔者采用的正弦曲线模型如图2所示。
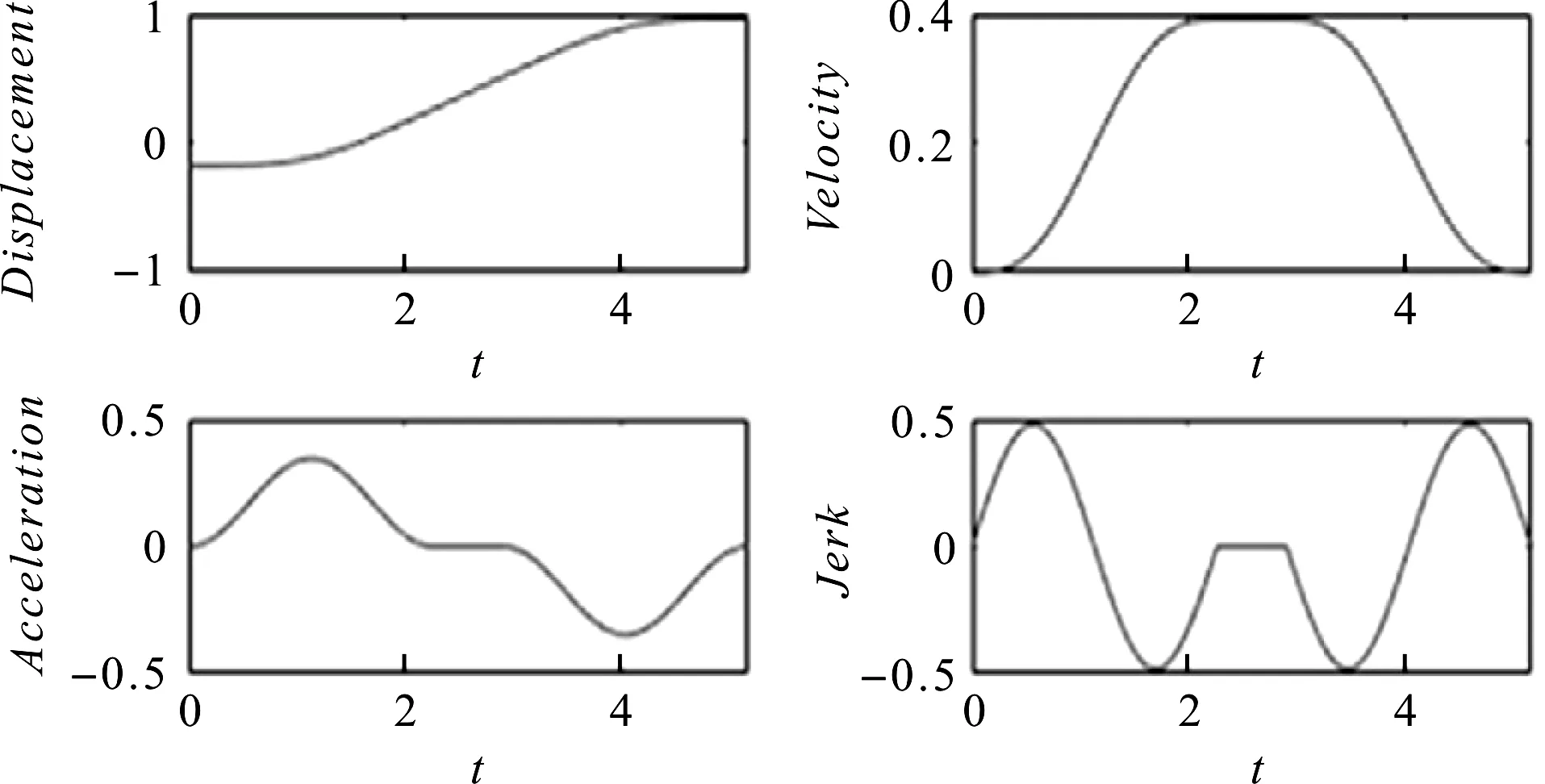
图2 模型中的加加速度、加速度、速度和位移
由图2可以推出单个电机轨迹表达式为:
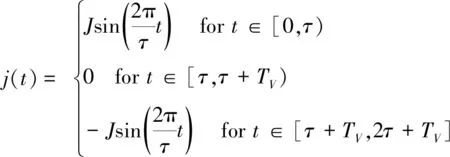
(1)
式中:J—加加速度峰值;τ—加速时间;TV—恒定速度时间;2π/τ—正弦波角频率。
该轨迹表现出非常高的规律性,但它允许利用少量参数将位移、速度和加速度轨迹参数化,并通过适当的优化方法对其值进行定义。
1.3 运动轨迹关节优化
笔者将D定义为单个关节的总需求(角度)位移。结合式(1)描述的加加速度轨迹和一些代数运算,可获得以下关键运动参数表达式:
(2)
(3)
(4)
式中:A—峰值加速度;V—峰值速度;TV—恒定速度时间。
为了执行最平滑的轨迹并避免对机器人手臂产生不必要的压力或振动,可使所有关节的运动轨迹实现同步,以便其能够同时开始和结束运动。同时,要求关键量(加加速度、加速度、速度)始终小于固定值。为此,笔者设计了一个非线性约束优化问题,该问题一次考虑所有n个关节的运动轨迹,并利用运动链中相对关节位置的运动能力(指数为i=1,…,n)以及具体任务要求(指数为j=1,…,nt)。
笔者重新将相关变量参数化为总运动时间函数T=2τ+TV和n加速时间τ=τ1,…,τn函数。因为,总运动由恒速阶段和对称加速和减速阶段组成,由此可以得出:
TVi=T-2τi
(5)
令i=1,…,n,将式(4,5)进行对比,可以将加加速度表示为T和τi的函数:
(6)
用一个新表达式代替公式(2~4)中的加加速度表达式,可以建立以下优化问题,该问题由以下目标函数构成:
对于某一任务m=1,…,nt,
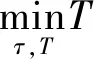
(7)
受限于:
T≥0
(8)
τi≥0
(9)
(10)
(11)
(12)
TV(T,τi)=T-2τi
(13)
总执行时间T对所有关节都通用,而各关节的加速时间τi则是不同的。
笔者所提机械手的最优轨迹规划方法如图3所示。

图3 机械手的最优轨迹规划方法
由图3可以看出,在n个关节的运动轨迹上同时开始和结束运动,但由于同步是优化的约束条件(所有关节在同一时间T完成运动),控制参数自动调整于最佳可接受性能,而不是简单地将所有轨迹重新调整到最慢速度。
PERUMAAL S等人提出的运动同步策略与本文提出方法得到的关节加加速度轨迹,如图4所示。
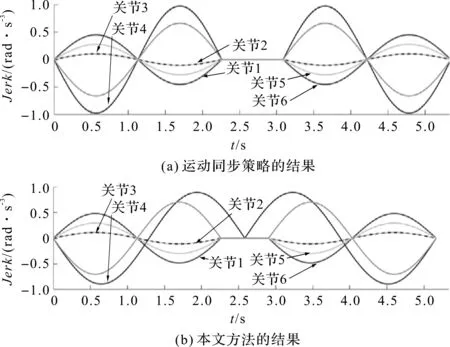
图4 两种方法得到的6个关节加加速度轨迹
从图4可以看出:通过本文方法的异步处理能力能够更好地利用关节性能,从而缩短执行时间;目标函数呈线性,且在凸约束下减到最小,因此任何局部最小值都可以看作全局最小值。
式(7~13)允许应用自定义关节管理方法,在“退化”模式下执行操作,将工作负载重新分配给性能更好的电机。
2 实验与结果分析
笔者以光电子产品的6 DoF机械手精密组装为测试案例对所述方法进行评估,并与现有多种规划方法(运动同步策略、近似时间最优策略和二维惩罚策略[14])进行对比。
具体测试环境如图5所示。

图5 具体测试环境
两个测试任务的相关参数如表1、表2所示。

表1 任务1的相关参数设置
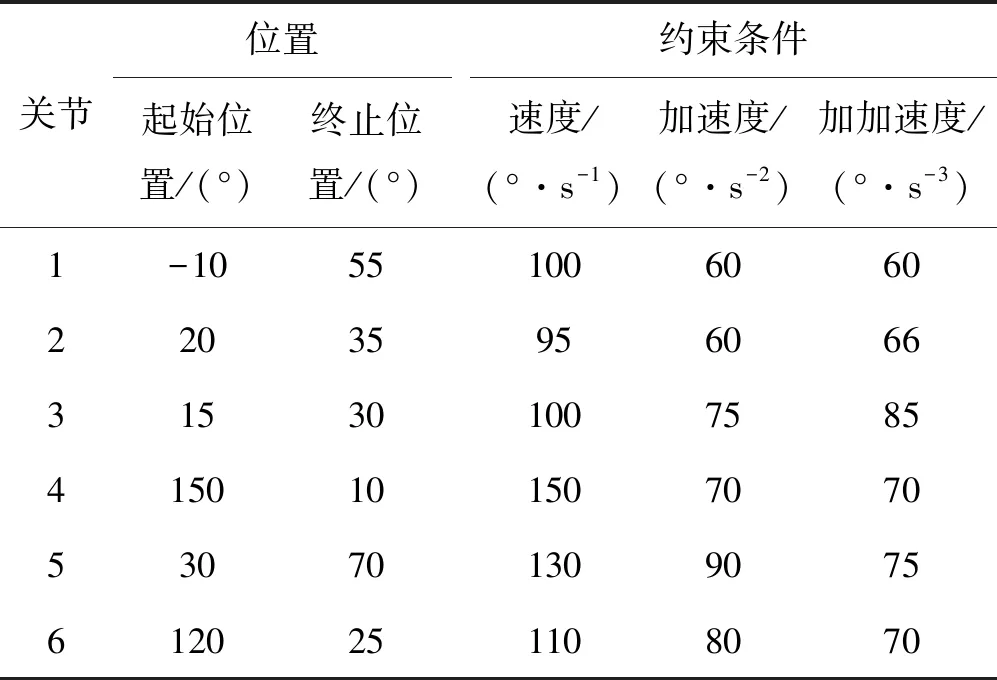
表2 任务2起始/终止位置和运动学限制
针对上述两个任务,不同轨迹规划方法获得的轨迹生成结果如表3所示。
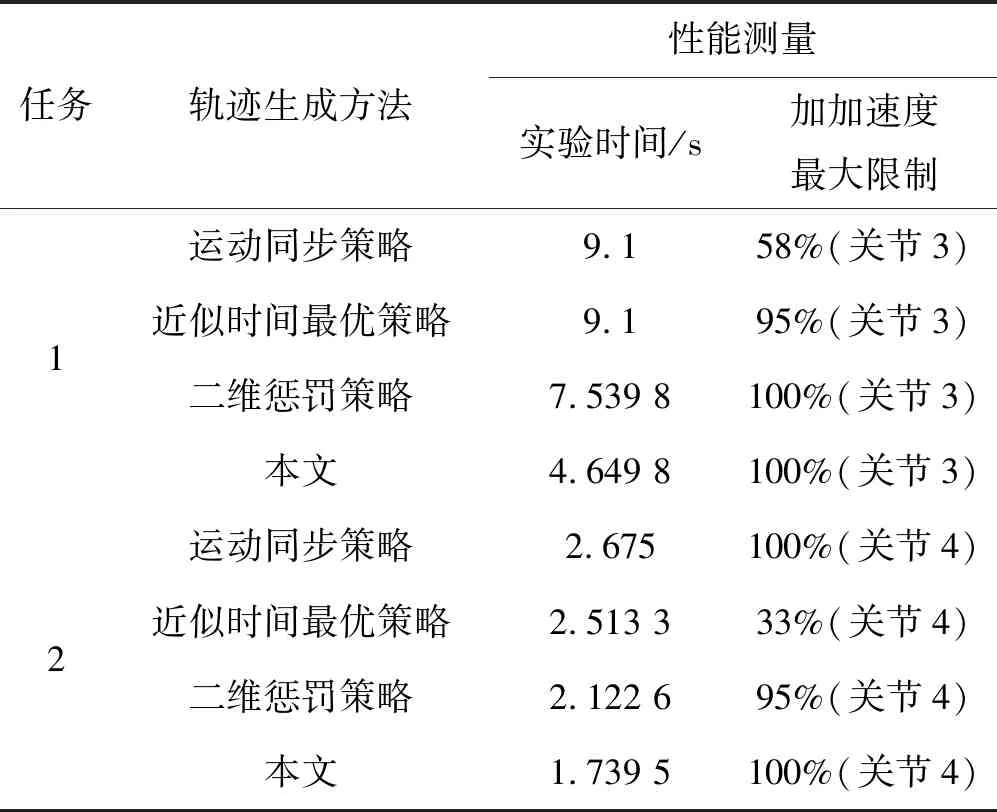
表3 参考任务对比结果
从表3可以看出:与所有其他方法相比,利用笔者方法所产生的执行时间最短。这是因为该方法通过促进各个关节达到最佳性能以实现执行时间最短,而且不会违反任何给定的约束条件。例如,对于任务1,产生的执行时间比运动同步策略获得的执行时间低39%。
两种算法在机械手上获得的运动轨迹与使用所提方法得到的运动轨迹对比,如图6所示。
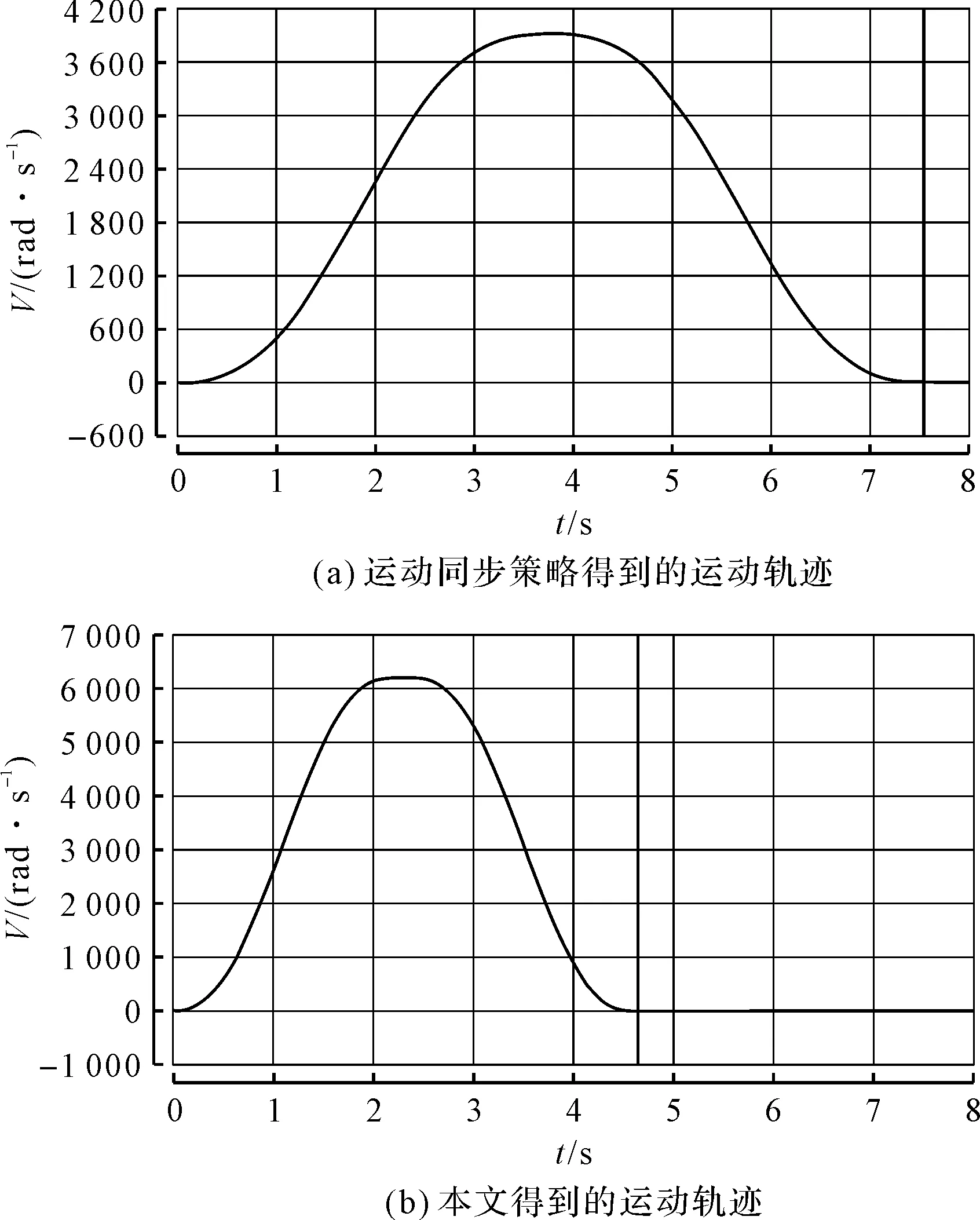
图6 任务1不同方法在关节3上生成的速度曲线
从图6可以看出:两者均得到了较好质量的平滑轨迹效果,然而本文方法展示了用以执行更快运动的不同运动学极限。本文方法的最高速度达到6 000 rad/s左右,而运动同步策略方法的最高速度在3 600 rad/s附近。这是因为后者以相对保守的方式将所有关节加速率同步到最慢,来生成平滑轨迹。而本文允许异步加速,且仅对总运动时间进行限制(没有限制每个关节的速度,加加速度最大限制为100%),从而充分发挥了关节性能。
笔者所提方法重点关注具体关节,因此其能够对关节的退化模式进行正确管理,这在精密组装行业非常重要。
其在任务2上的退化关节性能如表4所示。
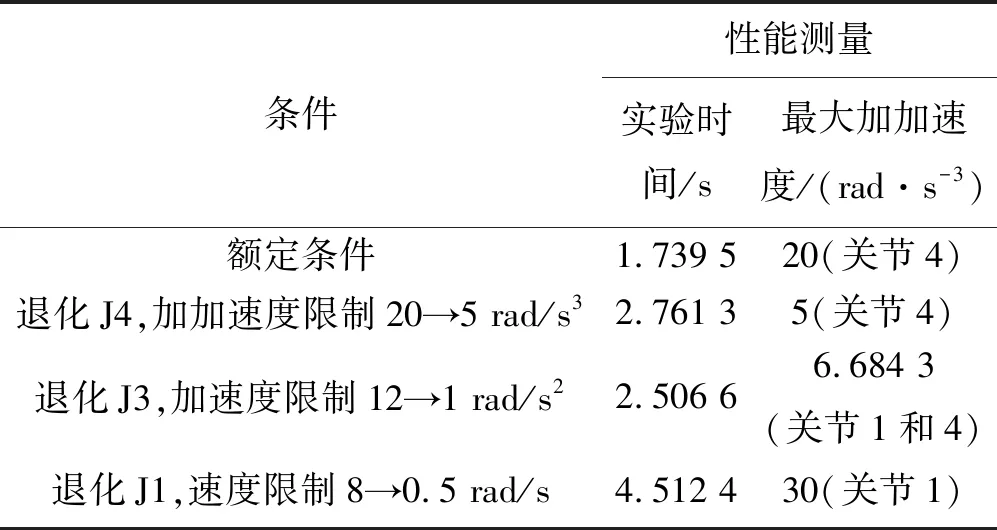
表4 退化关节性能(任务2)
从表4可以看出,即使在“退化”模式下,所提方法仍表现出令人满意的性能。这是由于执行时间是通过同时考虑所有关节进行优化的,需对关节的个体表现进行调整,以便更好地适应整体同步。
3 结束语
本文提出了一种适用于健康和退化状态的平滑运动轨迹规划方法,可应用于任何类型的机器人运动链;该轨迹规划方法通过在机器人机械手的所有关节上同时优化执行时间,实现了异步加速。
测试结果表明,该方法的执行时间相比现有的方法缩短了39%,并在给定运动约束条件下能够保持运动轨迹平滑;即使在“退化”模式下,执行时间仅提高1 s左右,保持5 rad/s3以上。
因此,该方法对高精度装配工业机器人作业系统具有较大的参考和应用价值。

