基于某汽车驱动桥壳预应力模态灵敏度的优化设计*

张 军

(江阴职业技术学院 机电工程系,江苏 江阴 214405)

0 引 言

汽车的底盘包括传动系统、行驶系统、转向系统和制动系统。而驱动桥在动力传动中起到至关重要的作用。驱动桥主要包括主减速器、差速器、半轴和万向节、桥壳等[1-2]。其中,驱动桥壳主要用于支撑和保护主减速器、差速器、半轴等,使左、右驱动车轮的轴向相对位置固定。

对于驱动桥壳的设计和分析,国内外很多学者已做了大量的研究。雷刚等[3]利用拓扑优化技术,在满足结构的强度和刚度要求的前提下,对某重型汽车的驱动桥壳进行了轻量化设计;孟佳欣[4]以板簧座附近的结构形状为参考,建立了优化目标函数,在最大垂向力、最大牵引力、最大制动力和最大侧向力的工况下,以应力-强度干涉理论为基础,对结构进行了优化设计;楼益强等[5]为研究驱动桥壳在动态载荷下的应力状况,分析了桥壳各点的应力分步和最大应力点的位置,进行了驱动桥壳变形计算;STEVEN W B[6]基于断裂力学理论对驱动桥壳的破坏进行了研究,发现了断裂主要发生在弹簧挡块与壳体焊接处。

但是,以上对驱动桥壳的分析都是基于对结构做静态、动态分析或优化,并没有考虑模态对于结构的影响。而模态是结构的全局特性,更是结构动力学分析的基础。

本文基于对驱动桥壳的预应力模态低阶频率的优化设计,以提高模态低阶频率为目标,桥壳质量不大于65 kg为约束,研究基于设计参数的模态灵敏度的影响因素,得到最优的结构参数;在此基础上,校核结构的强度和刚度特性。

1 驱动桥壳模态频率灵敏度分析

结构动力学分析是用来确定惯性和阻尼起重要作用时结构动力学行为的技术[7-9]。在汽车行驶过程中,驱动桥壳的运行工况十分复杂,比如路面的不平度引起的冲击力、紧急制动时的制动力,牵引力等。而大部分外载都处于低频振动状态,所以需尽量提高驱动桥壳的低阶固有频率,从而避免外载对桥壳的影响。通过对驱动桥壳模态灵敏度的研究,发现影响低阶固有频率的关键结构参数,可以通过优化结构,避免共振影响造成的结构性破坏。

1.1 模态频率灵敏度

通过对结构做模态分析,可以预知结构各阶主要振型的特性,从而可以预测结构各频段内在各种振源作用下的响应。而模态频率的灵敏度是指结构各阶振动频率随结构参数的变化率。

对于无阻尼结构自由模态分析,振动方程如下:

(1)

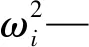
将式(1)对x求偏导,可得:

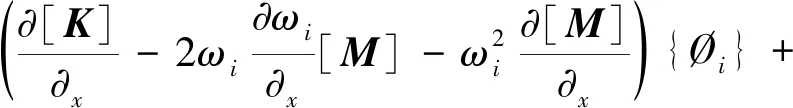
(2)

式中:x—结构设计变量。

根据式(1),且用{φi}T左乘式(2),可得:

(3)

第i阶模态频率对设计变量x的灵敏度为:

(4)

对于无阻尼预应力模态灵敏度分析方程,式(1)右边将0更改为预应力{Fi},如下式:

(5)

同样根据上述推导方式,可得到其第i阶模态频率对设计变量的灵敏度。

1.2 驱动桥壳预应力模态分析

汽车正常行驶时,其振源和振动方式非常复杂,通常是由路面不平造成的,其激励频率范围为0～50 Hz。而发动机和传动系是低频激励,所以汽车驱动桥壳的低阶固有频率应该高于50 Hz,以避免引起共振[10]。

为了真实反映实际工作状态,笔者对桥壳做预应力模态分析。

1.2.1 驱动桥壳受力分析

以某轻型货车为研究对象,车型为(4×2)单胎结构,整备质量为2 500 kg,最高车速120 km/h,轮距1 600 mm,满载轴荷3 650 kg。货车主要采用整体式的驱动桥壳,因为整体式桥壳与其他结构相比,结构的刚度和强度相对较大,且作为整体式结构,便于主减速器、差速器、半轴等的安装和维修。汽车行驶过程中,驱动桥壳受力主要包括垂向力、侧向力、牵引力、制动力。

笔者参考QC/T533-1999《汽车驱动桥台架试验方法》[11-12](主要适用于载货量8 t以下的载货汽车及其相应的越野车和大客车的驱动桥,简称《试验方法》)中的要求施加载荷和边界条件,并对分析结果作评价。

在《试验方法》中,驱动桥壳垂直弯曲强度试验的主要评价参数为失效(断裂或严重塑性变形)后备系数,即:

式中:Kn—垂直弯曲破坏后备系数;Pn—垂直弯曲破坏载荷;P—满载轴荷。

试验中,要求加载到最大负荷后,继续加载直至结构失效破坏,记录此时的失效(断裂或严重变形)载荷,要求失效后备系数大于6。桥壳的轴荷3 650 kg,即Pn垂直弯曲破坏载荷要大于等于3 650×6×10=219 000 N,两侧的弹簧座各受载荷至少要109 500 N,所以在做受力分析时,直接在两侧的弹簧座施加载荷109 500 N,来预测结构的垂直弯曲强度。

根据《试验方法》中的要求,试验时,桥壳放平,力点为二钢板弹簧中心,支点为该桥轮距的相应点。或者将力点和支点位置互换[13-19]。安装时,加力方向应与桥壳轴管中心线垂直,支点应能滚动,以适应加载变形不致运动干涉。测点位置不少于7点。

建立边界条件时,将桥壳看做简支梁,因为台架试验时的支点为面接触,利用远端点约束桥壳半轴套管左轮距位置的下面,驱动桥壳边界条件如图1所示。

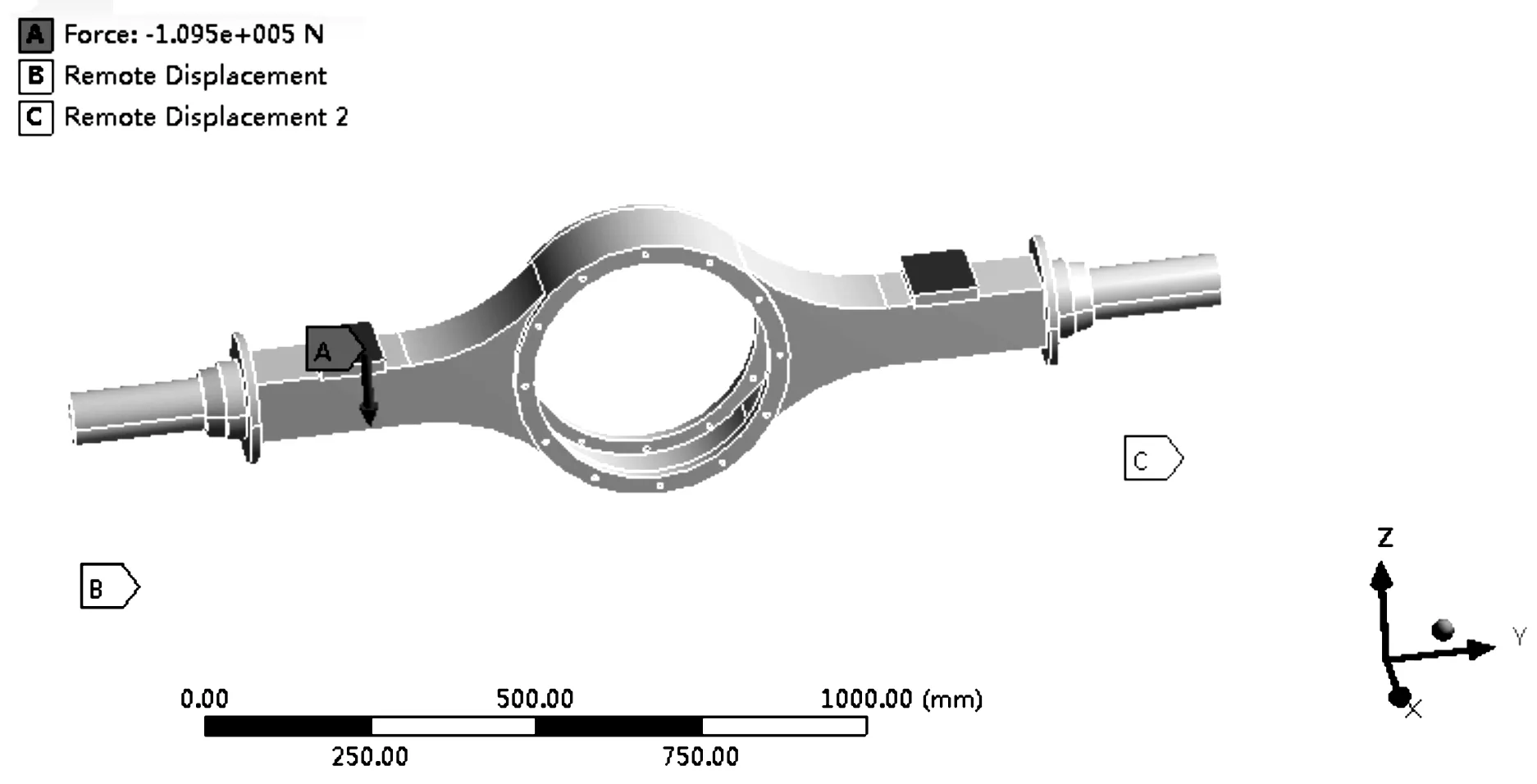
图1 驱动桥壳边界条件

约束x、y、z方向的位移和沿y轴的转动,桥壳的半轴套管右轮距位置的下面通过远端点约束x、z的位移和沿y轴的转动。驱动桥壳材料SCW550,屈服强度420 MPa,抗拉强度570 MPa,延伸率≥15%,弹性模量212 GPa,泊松比0.31,密度7.85 g/cm-3。所得结构最大应变为6.27 mm,最大应力为325.8 MPa,远小于结构的抗拉强度570 MPa,即满足桥壳垂直弯曲强度要求。

1.2.2 驱动桥壳预应力模态分析

驱动桥壳的模态分析包括桥壳的固有频率和振型,是桥壳动力学分析的基础。

以受力分析结果作为预应力输入条件,对驱动桥壳做预应力模态分析,驱动桥壳前6阶模态如表1所示。

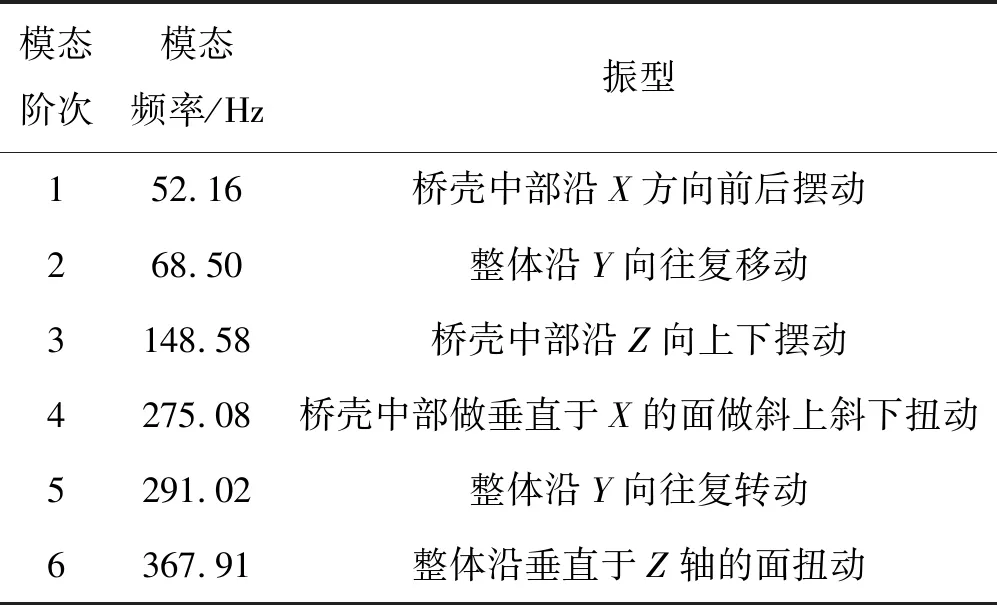
表1 驱动桥壳前6阶模态

上述分析可知:低阶固有频率为52.16 Hz,非常接近50 Hz,即存在与外界激励发生共振的风险。所以需要通过改变关键尺寸参数来优化结构,以提高低阶模态频率。

1.3 驱动桥壳基于设计变量的模态灵敏度分析

基于不同的设计参数,笔者分别以左右侧弹簧座厚度、左右侧半轴套管半径、桥壳前后孔半径、左右半轴端面厚度为关键设计变量,以整体质量不大于65 kg为约束条件,对驱动桥壳做模态频率的灵敏度分析,从而对结构做优化设计,提高结构的低阶固有频率。

设计参数尺寸变量如表2所示。

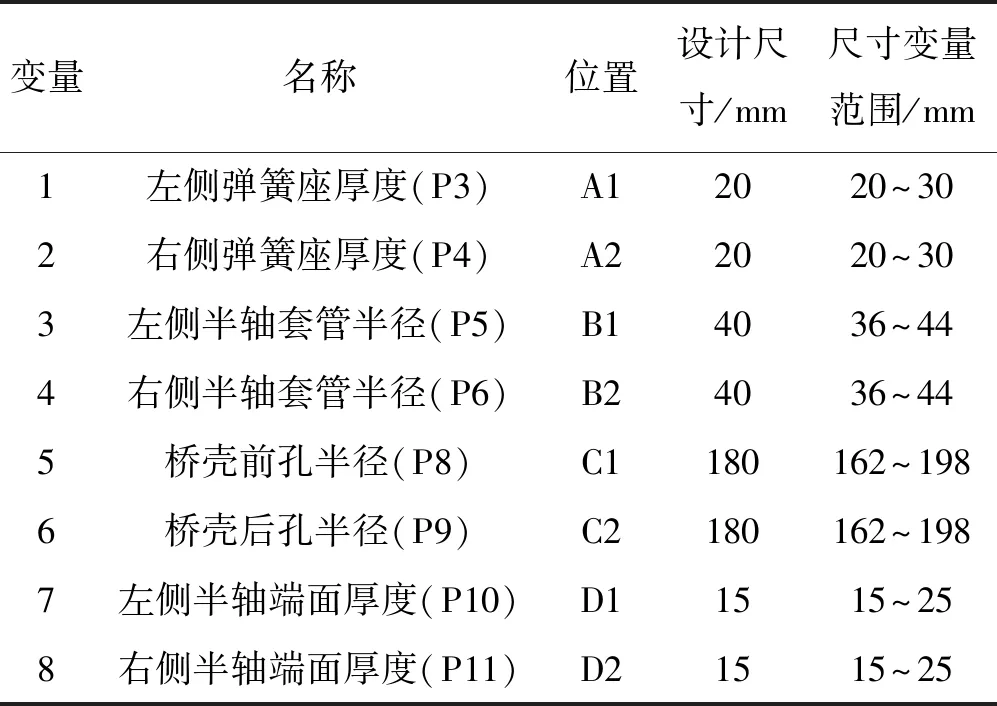
表2 设计参数尺寸变量

桥壳设计参数位置如图2所示。

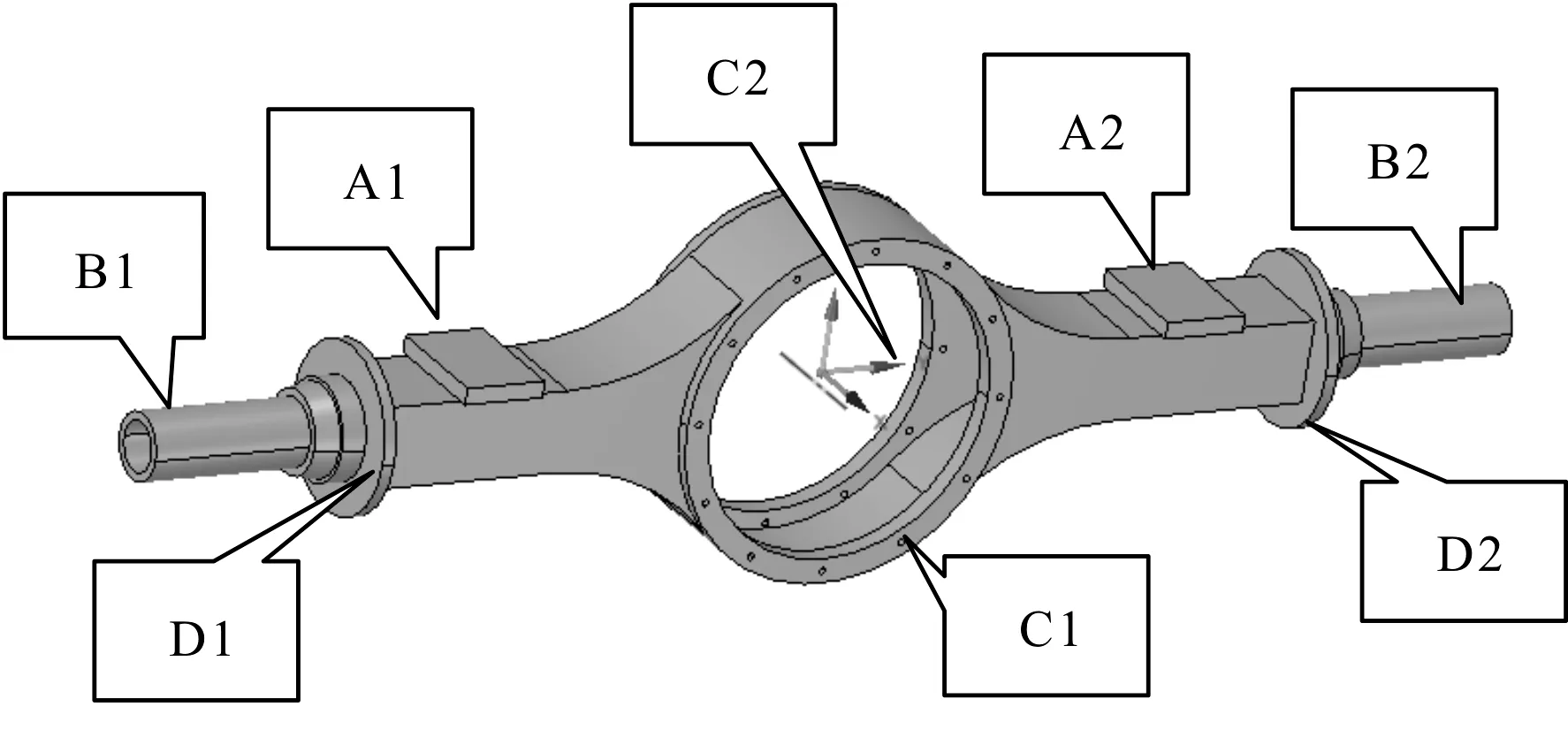
图2 桥壳设计参数位置

考察灵敏度分析结果,低阶模态频率对应设计变量的灵敏度如图3所示。

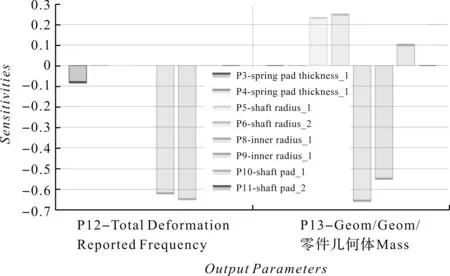
图3 低阶模态频率对应设计变量的灵敏度

当灵敏度为正值时,结构的参数值越大,低阶模态频率的灵敏度越高,即模态频率值越大;反之,当灵敏度为负值时,结构的参数值越小,低阶模态频率的灵敏度越高,即模态频率越高。由模态灵敏度分析结果可知：

(1)对低阶模态频率影响最大的是桥壳的前、后内孔半径,即是主减速器与传动轴的接口部位。模态灵敏度为负值,说明桥壳内孔半径越小模态低阶频率越大,且桥壳质量越大。前、后内孔半径对低阶模态频率的影响程度基本相同；

(2)左侧的弹簧座厚度减少,低阶频率增加。但右侧的弹簧座厚度对低阶频率没有影响。左、右侧弹簧座厚度对桥壳质量基本没有影响；

(3)左、右侧半轴套管半径增加,会使桥壳质量随之增加,但对低阶模态频率没有影响；

(4)左、右侧半轴端面厚度对低阶模态频率没有影响,左侧厚度增加桥壳质量增加,右侧厚度增加,桥壳质量不变。

前内孔半径与低阶模态频率关系如图4所示。

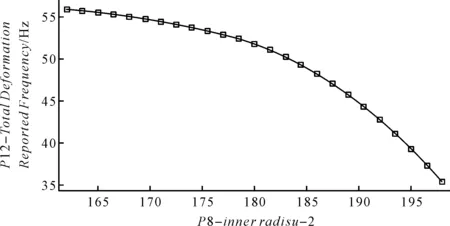
图4 前内孔半径与低阶模态频率关系

后内孔半径与低阶模态频率关系如图5所示。

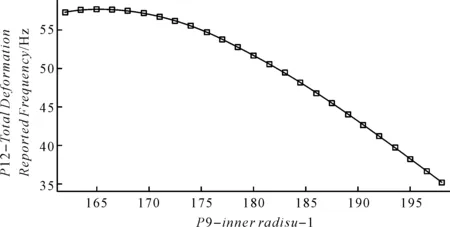
图5 后内孔半径与低阶模态频率关系

由图5可以看到:随着内孔半径的增加,低阶模态频率呈近似抛物线逐渐减小。

2 驱动桥壳模态优化设计

2.1 模态优化设计方程

模态优化设计,是以提高低阶模态频率为目标,以保持桥壳质量不大于上限值为约束条件,通过求解不同的结构参数建立的响应面而获得,其数学模型如下:

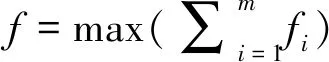
(6)

xjb≤xj≤xju,f=1,2,…,n

式中:f—壳体低阶模态频率;fi—壳体第i个低阶模态频率;M—壳体质量;Mmax—质量上限;xj,xjb,xju—桥壳的结构设计变量、设计变量下限和设计变量上限。

该优化分析中,设计变量分别取左右侧弹簧座厚度、左右侧半轴套管半径、桥壳前后孔半径、左右半轴端面厚度。考虑到分析的时间和效率,优化分析只以提高桥壳的低阶模态频率为目标,后续再对优化结果做强度、刚度方面的校核。

2.2 桥壳模态优化分析

笔者根据上面的设计变量,建立响应面优化模型。即利用中心复合设计方法生成样本点,然后利用标准响应面的完全的二次多项式方法根据获得的样本点拟合出响应面,最后获得结构的优化结果。优化结果低阶模态频率66.888 Hz,桥壳质量61.016 kg,此时对应的设计参数分别为左、右侧弹簧座厚度20.005 mm,左、右侧半轴套管半径36.004 mm,桥壳前、后孔半径162.02 mm,左、右侧半轴端面厚度15.005 mm。

2.3 桥壳模态灵敏度优化设计

根据模态灵敏度分析结果,对于低阶模态频率影响最大的设计参数是桥壳前后内孔半径,而左、右侧半轴套管半径的减小会引起桥壳质量的降低。另外,考虑驱动桥壳与内、外部结构的装配关系,取桥壳前后内孔半径C1=C2=162 mm,左、右侧半轴半轴套管半径B1=B2=36 mm为结构参数优化结果,然后再次对桥壳做预应力模态分析。

优化后驱动桥壳前6阶模态如表3所示。

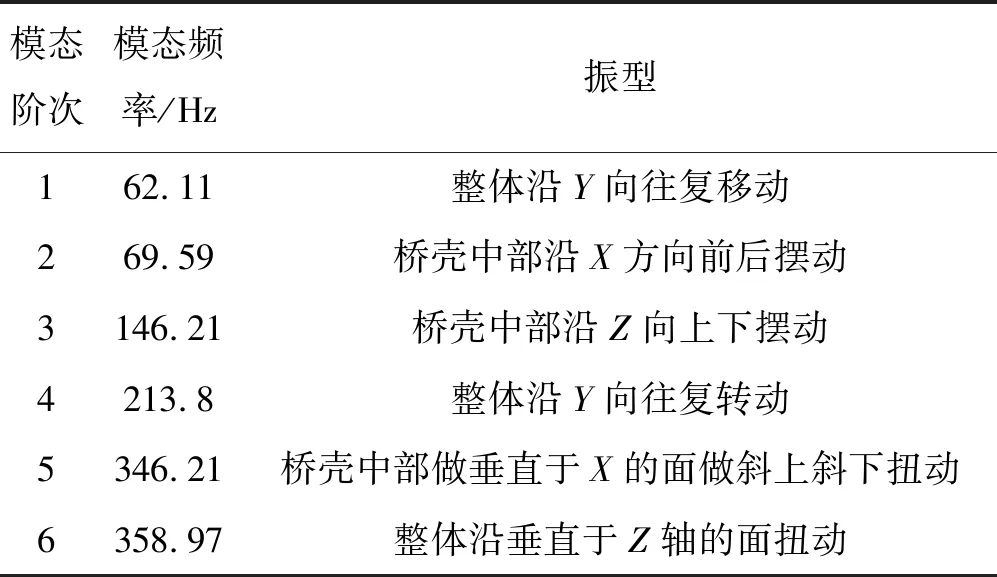
表3 优化后驱动桥壳前6阶模态

从表3中可知:低阶模态频率由52.16 Hz增加到62.11 Hz,完全可以避开外界激励频率范围(0～50 Hz)。优化的结果不但改变了低阶模态频率,还改变了前五阶振型,这是因为桥壳结构优化后,系统质量矩阵和刚度矩阵都有改变,对应的各阶特征值和特征向量也会改变。

3 优化后强度与刚度校核

根据《试验方法》,驱动桥壳的垂直弯曲静强度和垂直弯曲刚性是驱动桥壳的最关键也是最基本的评价指标。所以,主要对这两个指标做静强度和刚度校核分析。

3.1 驱动桥壳垂直弯曲静强度分析

根据《试验方法》中驱动桥壳垂直弯曲静强度试验的试验要求,对驱动桥壳的优化后的模型做弯曲静强度分析,可得最大应变为5.23 mm,最大应力为321.46 MPa,远小于结构的抗拉强度570 MPa,且低于优化前的分析结果。

3.2 驱动桥壳垂直弯曲刚性分析

在《试验方法》中要求在满载轴荷时,桥壳最大位移点与轮距之比的数值不超过1.5 mm/m。该轻型货车的满载轴荷为36 500 N,所以两端的弹簧座各施加载荷18 250 N,约束条件与计算垂直弯曲静强度时相同,分析结果最大应变为0.86 mm,最大应力为52.76 MPa。桥壳最大位移点与轮距之比为0.86 mm/1.6 m=0.54 mm/m<1.5 mm/m,所以满足垂直弯曲刚性要求。

4 驱动桥壳垂直弯曲静强度与刚性试验

根据《试验方法》,搭建试验台架,驱动桥壳垂直弯曲静强度试验和垂直弯曲刚性试验如图6所示。

图6 驱动桥壳垂直弯曲静强度试验和垂直弯曲刚性试验

垂直弯曲静强度试验中,当桥壳两侧弹簧座外载荷分别为109 500 N时,经过10次往复试验,均为发生断裂。垂直弯曲刚性试验中,当桥壳两侧弹簧座外载荷分别为18 250 N时,桥壳最大变形为0.74 mm,与仿真分析结果误差为14%。

5 结束语

本文以某货车的驱动桥壳为分析对象,建立了其振动微分方程,并推导出基于设计变量的模态灵敏度分析方程,构建了驱动桥壳的优化设计数学模型；在此基础上,研究了货车驱动桥壳基于关键设计参数的模态灵敏度,并根据灵敏度分析结果,以提高低阶模态频率为目标,以结构整体质量不大于65 kg为约束条件,建立了优化模型。

由优化结果可知,低阶模态提高了10 Hz,满足设计要求。

最后,通过仿真分析和台架试验校核优化结果,优化结果满足垂直弯曲静强度和垂直弯曲刚性要求。